[NOI2016]优秀的拆分

传送门

我们把\(AABB\)串拆成两个部分，前一部分是\(AA\),后一部分是\(BB\)

此时我们考虑统计两部分内容:\(f[i]\)表示以\(i\)开头的\(AA\)形式的串数量，\(g[i]\)表示以\(i\)结尾的\(AA\)形式的串的数量

考虑一下\(SA\)

我们枚举一下\(A\)的长度\(len\)，然后再枚举\(len\)的倍数位置

求出当前节点和\(i+len\)两个节点对应子串的\(lcp\)和\(lcs\)

\(Gypsophila\)聚聚的图，侵删

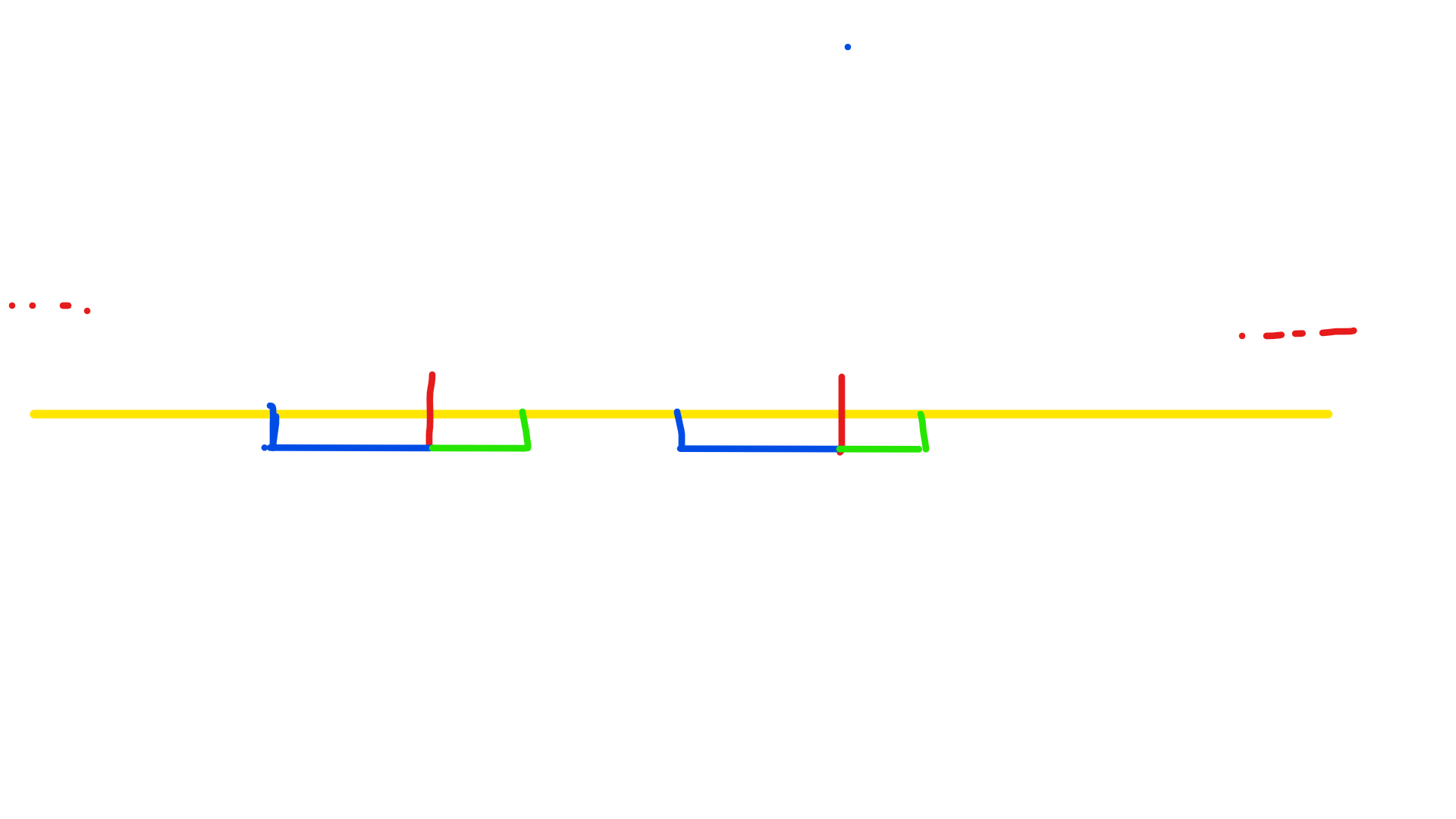
红色对应两个节点，绿色是\(lcp\)，蓝色是\(lcs\)

显然这样的没有贡献的，如果\(i\)的\(lcp\)和\(i+len\)的\(lcs\)有交

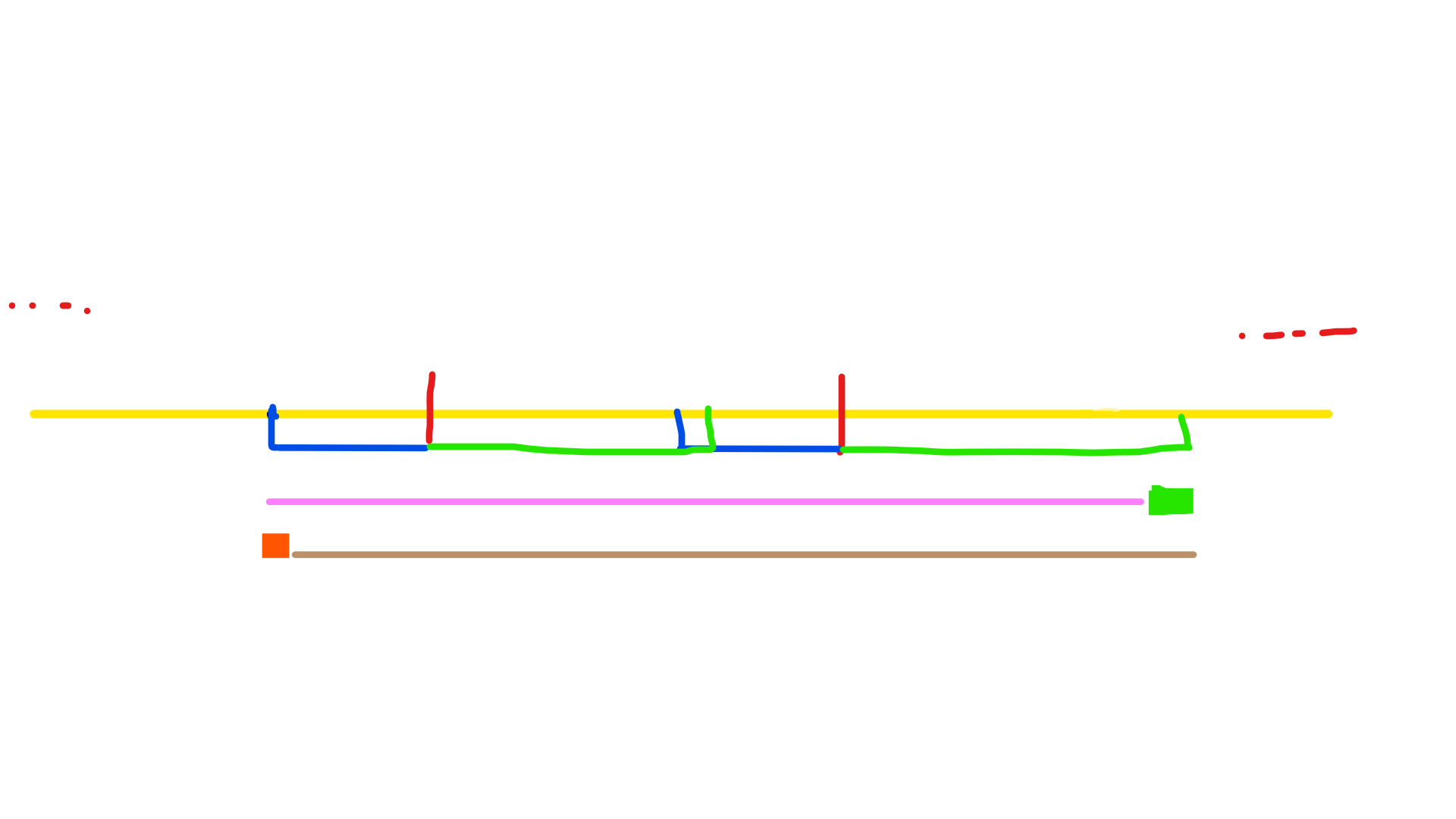
那么粉色到棕色的位置显然都会有一个答案的贡献，我们用差分统计出来

问题就解决啦，实现起来细节不少

#include<bits/stdc++.h>
using namespace std;
namespace red{
#define int long long
#define ls(p) (p<<1)
#define rs(p) (p<<1|1)
#define mid ((l+r)>>1)
#define y1 qwq 
	inline int read()
	{
		int x=0;char ch,f=1;
		for(ch=getchar();(ch<‘0‘||ch>‘9‘)&&ch!=‘-‘;ch=getchar());
		if(ch==‘-‘) f=0,ch=getchar();
		while(ch>=‘0‘&&ch<=‘9‘){x=(x<<1)+(x<<3)+ch-‘0‘;ch=getchar();}
		return f?x:-x;
	}
	const int N=1e5+10,inf=1<<30;
	int haku,n,m,ret;
	char s[N];
	int lg[N],f[N],g[N];
	struct SA
	{
		int x[N],y[N],c[N],sa[N],rk[N],h[N];
		int f[N][21];
		inline void clear()
		{
			memset(x,0,sizeof(x));
			memset(y,0,sizeof(y));
			memset(c,0,sizeof(c));
			memset(sa,0,sizeof(sa));
			memset(rk,0,sizeof(rk));
			memset(h,0,sizeof(h));
			memset(f,0,sizeof(f));
		}
		inline void get_sa()
		{
			clear();m=‘z‘;
			for(int i=1;i<=n;++i) ++c[x[i]=s[i]];
			for(int i=1;i<=m;++i) c[i]+=c[i-1];
			for(int i=n;i;--i) sa[c[x[i]]--]=i;
			for(int k=1;k<=n;k<<=1)
			{
				int num=0;
				for(int i=n-k+1;i<=n;++i) y[++num]=i;
				for(int i=1;i<=n;++i) if(sa[i]>k) y[++num]=sa[i]-k;
				for(int i=1;i<=m;++i) c[i]=0;
				for(int i=1;i<=n;++i) ++c[x[i]];
				for(int i=1;i<=m;++i) c[i]+=c[i-1];
				for(int i=n;i;--i) sa[c[x[y[i]]]--]=y[i],y[i]=0;
				swap(x,y);
				x[sa[1]]=1,num=1;
				for(int i=2;i<=n;++i)
					x[sa[i]]=(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])?num:++num;
				if(num==n) break;
				m=num;
			}
			int k=0;
			for(int i=1;i<=n;++i) rk[sa[i]]=i;
			for(int i=1;i<=n;++i)
			{
				if(rk[i]==1) continue;
				if(k) --k;
				int j=sa[rk[i]-1];
				while(j+k<=n&&i+k<=n&&s[i+k]==s[j+k]) ++k;
				h[rk[i]]=k;
			}
			for(int i=1;i<=n;++i) f[i][0]=h[i];
			for(int i=1;i<=20;++i)
			{
				for(int j=1;j+(1<<i)-1<=n;++j)
				{
					f[j][i]=min(f[j][i-1],f[j+(1<<(i-1))][i-1]);
				}
			}
		}
		inline int getlcp(int l,int r)
		{
			if(l>r) swap(l,r);
			++l;
			int k=lg[r-l+1]-1;
			return min(f[l][k],f[r-(1<<k)+1][k]);
		}
	}sa1,sa2;
	inline void main()
	{
		haku=read();
		for(int i=1;i<N;++i) lg[i]=lg[i>>1]+1;lg[0]=1;
		while(haku--)
		{
			scanf("%s",s+1);n=strlen(s+1);ret=0;
			sa1.get_sa();
			reverse(s+1,s+n+1);
			sa2.get_sa();
			memset(f,0,sizeof(f));
			memset(g,0,sizeof(g));
			for(int len=1;len<=n/2;++len)
			{
				for(int i=len;i+len<=n;i+=len)
				{
					int l=i,r=i+len;
					int lcp=min(len,sa1.getlcp(sa1.rk[l],sa1.rk[r]));
					l=n-r+2,r=n-i+2;
					int lcs=min(len-1,sa2.getlcp(sa2.rk[l],sa2.rk[r]));
					if(lcp+lcs>=len)
					{
						++f[i-lcs];--f[i-lcs+(lcp+lcs-len)+1];
						++g[i+len+lcp-(lcp+lcs-len+1)];--g[i+len+lcp];
					}
				}
			}
			for(int i=1;i<=n;++i) f[i]+=f[i-1],g[i]+=g[i-1];
			for(int i=1;i<n;++i) ret+=g[i]*f[i+1];
			printf("%lld\n",ret);
		}
	}
}
signed main()
{
	red::main();
	return 0;
}

[NOI2016]优秀的拆分

原文：https://www.cnblogs.com/knife-rose/p/12683132.html