公式:
几何解释:对 2D 向量 v ,能构造一个以 \(v\) 为斜边的直角三角形,直角边的长度分别为分量 \(v_x\) ,\(v_y\) 的绝对值,斜边长度即为向量 \(v\) 的大小
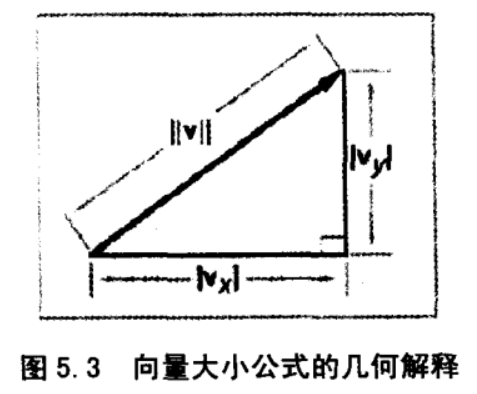
注意点
几何解释
注意点
几何解释
向量点乘就是对应分量乘积的和,其结果是一个标量
点乘满足交换律:\(a \cdot b = b \cdot a\)
几何解释
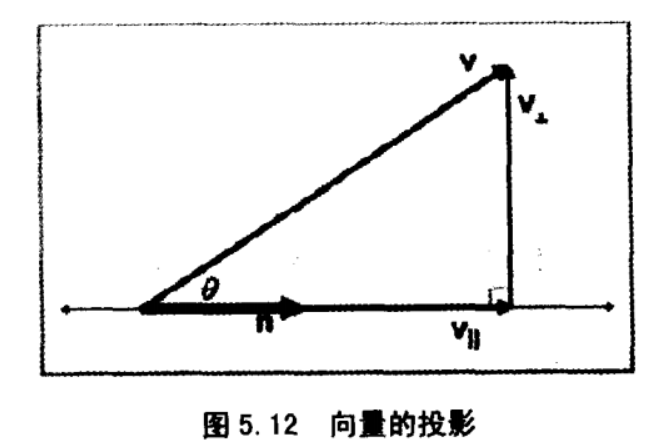
点乘等于向量大小与向量夹角的 cos 值的积:\(a \cdot b=||a|| ||b|| cos\theta\)
两向量的夹角:\(\theta=arccos(\frac{a\cdot b}{||a||||b||})\)
点乘的结果描述了两个向量的 “相似” 程度,点乘结果越大,两向量越相近
点乘结果的符号可大致确定 \(\theta\) 的类型
| a·b | Θ | 角度 | a 和 b |
|---|---|---|---|
| >0 | 0°≤Θ<90° | 方向基本相同 | |
| 0 | Θ≤90° | 正交 | |
| <0 | 90°<Θ≤180° | 方向基本相反 |
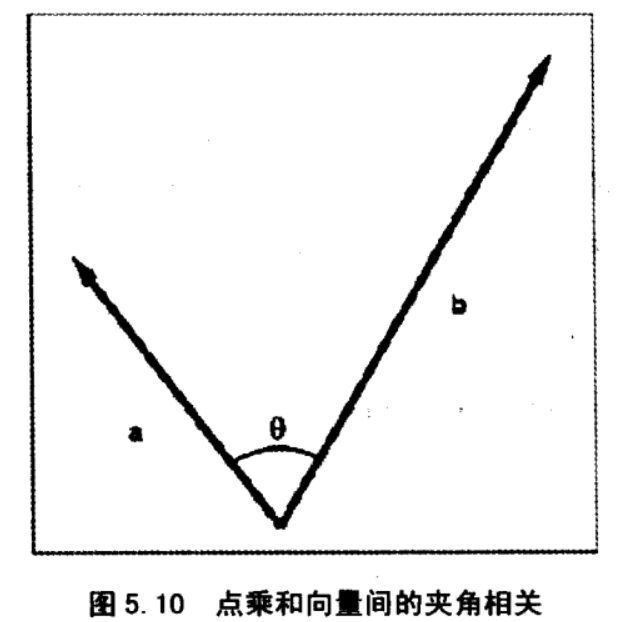
向量投影
给定两个向量 \(v\) 和 \(n\),能将 \(v\) 分解为两个分量:\(v_{\|}\) 和 \(v_{\perp}\) 。它们分别平行于和垂直于 \(n\),并满足 \(v=v_{\perp}+v_{\|}\)。称平行分量 \(v_{\|}\) 为 \(v\) 在 \(n\) 上的投影
使用点乘计算投影,几何解释:
\(\mathbf{v}_{\|}=\mathbf{n} \frac{\left\|\mathbf{v}_{\mathrm{u}}\right\|}{\|\mathbf{n}\|}\)
\(\begin{aligned} &\cos \theta=\frac{\left\|\mathbf{v}_{\|}\right\|}{\|\mathbf{v}\|}\&\cos \theta\|\mathbf{v}\|=\left\|\mathbf{v}_{\mathrm{\|}}\right\| \end{aligned}\)
所以:
\(\begin{aligned} \mathbf{v}_{\|} &=\mathbf{n} \frac{\|\mathbf{v}\| \cos \theta}{\|\mathbf{n}\|} \&=\mathbf{n} \frac{\|\mathbf{v}\|\|\mathbf{n}\| \cos \theta}{\|\mathbf{n}\|^{2}} \&=\mathbf{n} \frac{\mathbf{v} \cdot \mathbf{n}}{\|\mathbf{n}\|^{2}} \end{aligned}\)
叉乘仅可用于 3D 向量,叉乘得到一个向量,并且不满足交换律
计算公式
几何解释
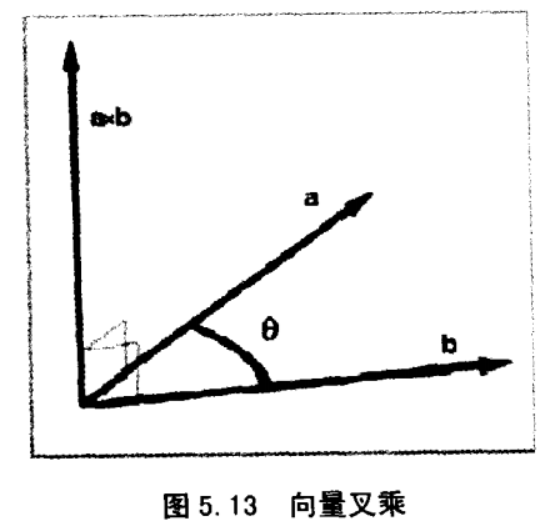
\(\mathbf{a} \times \mathbf{b}\) 的方向判断
叉乘的应用:创建垂直于屏幕、三角形或多边形的向量
原文:https://www.cnblogs.com/bky-hbq/p/12684022.html