1)概率论与贝叶斯先验
本福特定律:又称第一数字定律,是指在实际生活得出的一组数据中,以1为首出现的概率约为总数的三成;是直观现象1/9的三倍。
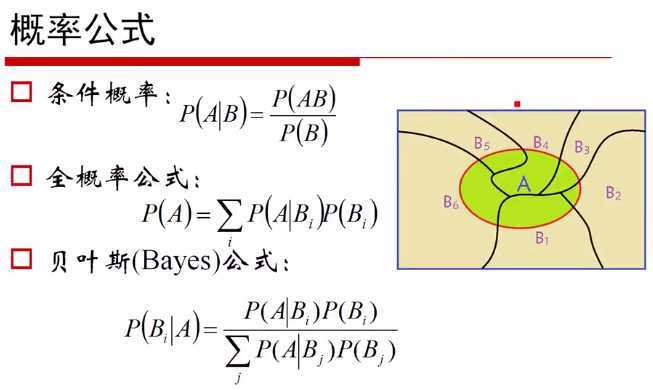
贝叶斯公式:给定某系统的若干样本X,计算该系统的参数。-28:13

分布-32:56
两点分布 0-1分布 -33:02

二项分布 -34:46




泊松分布-44:45
在实际实例中,当一个随机事件,以固定的平均速度显示速率λ(或称密度)随机且独立地出现时,那么这个时间在单位时间(面积或体积)内出现的次数或个数就近似地服从泊松分


均匀分布 -47:37

指数分布 -48:30


指数分布的无记忆性 -50:31

正态分布 -53:20



总结 -60:50
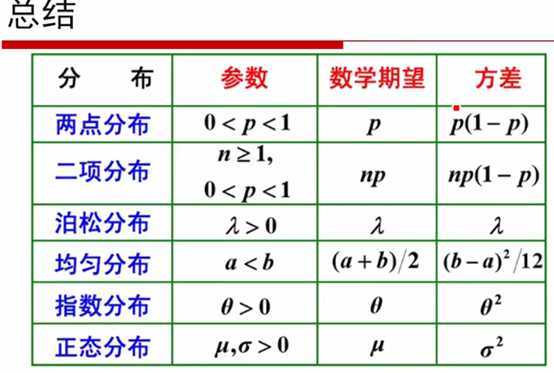
Beta分布-61:45


事件的独立性 -95:20



方差 -103:22

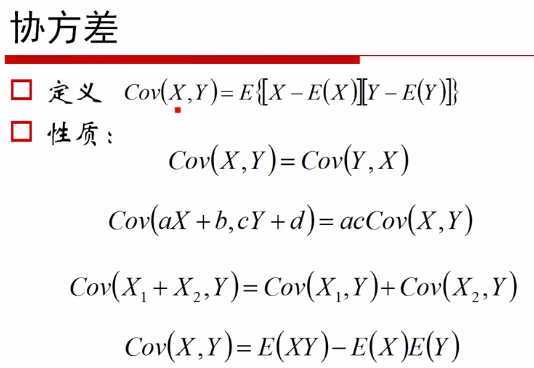



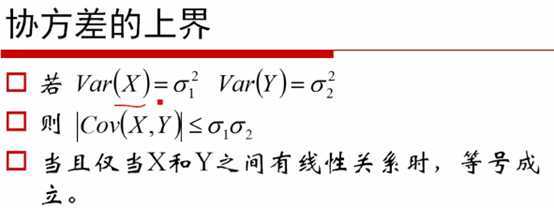
Pearson相关系数 -117:06

切比雪夫不等式 -137:51

大数定律 -138:28


伯努利定理 -142:56
中心极限定理 -143:41


2)矩阵和线性代数
原文:https://www.cnblogs.com/HvYan/p/12685837.html