动态规划的思想实质是分治思想和解决冗余,与分治算法类似将原问题分解成若干个子问题,先求解子问题,再从这些子问题的解得到原问题的解。不同于分治算法,经分解的子问题往往不是互相独立的,通过保存已解决的子问题的答案,避免对子问题重复计算、节省时间,也就是解决冗余。
那么动态规划解决的问题是什么样的呢?动态规划解决的问题一般是最优化问题,也就是比如最大子序和、最小编辑距离等最值问题,或者背包问题、打家劫舍等最优方案问题。这些问题有以下几个特点:
下面以经典的爬楼梯(LeetCode-70)为例,分析动态规划的问题特点以及基本思想。你正在爬一个有个N个台阶的楼梯,每次只能上1个或者2个台阶,那么到达顶端共有多少种不同的方法?
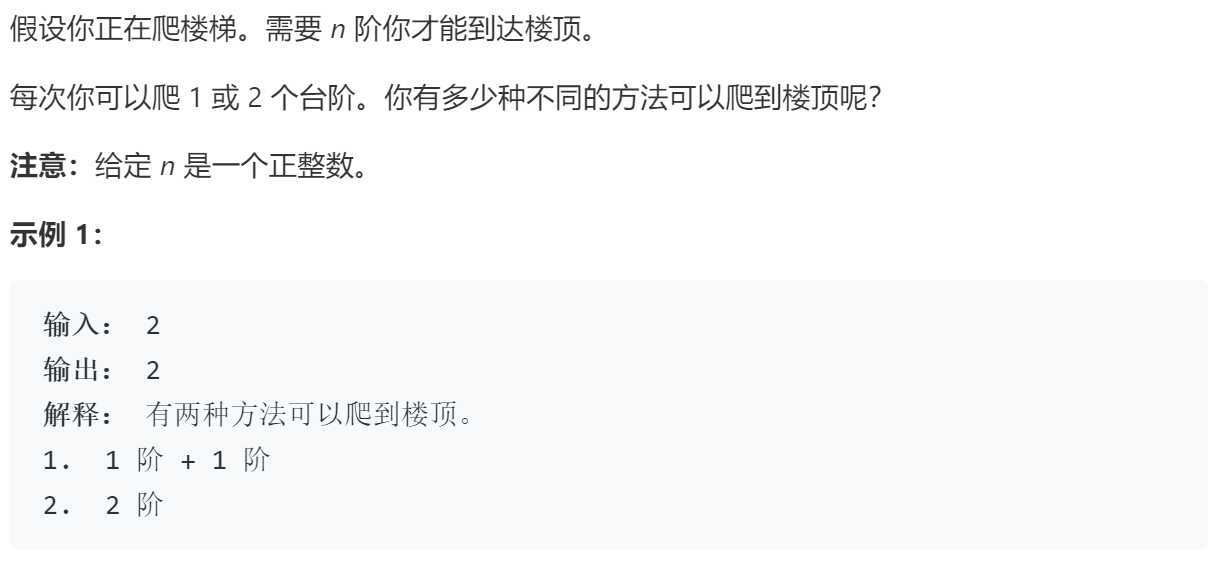
首先分析此问题是否符合动态规划问题,假设从0到达第N个台阶的方法共有f(N)个,到达N个台阶,有两种可能,第一种可能是从第N-1个台阶上1个台阶到达终点,第二种可能是从第N-2个台阶上2个台阶到达终点,则f(N) = f(N-1) + f(N-2)。这一点满足最优子结构性质,即原问题可分解成若干个子问题,当子问题得到最优解则原问题得最优解。由于f(N)与f(N+i)无关,其中i > 0,所以f(N)问题无后效性。我们可以通过递归求得f(N),代码如下:
int climbStairs (int n) { if (n == 0 || n == 1) return 1; return climbStairs (n - 1) + climbStairs (n - 2); }
假设N = 20,通过递归树可以发现,计算原问题f(20),需先计算出子问题f(19)和f(18),然后要计算f(19),需先算出子问题f(18)和f(17),以此类推直到f(1)或者f(2)返回结果,递归树不再向下生长了。显然递归树节点总数为指数级别,递归算法的时间复杂度为O(2^n),耗时严重。低效的原因在于存在大量重复计算,比如f(18)被计算了两次,导致大量的耗时,并且之后每个子问题基本都被重复计算。所以此问题满足动态规划另一种性质:重叠子问题。
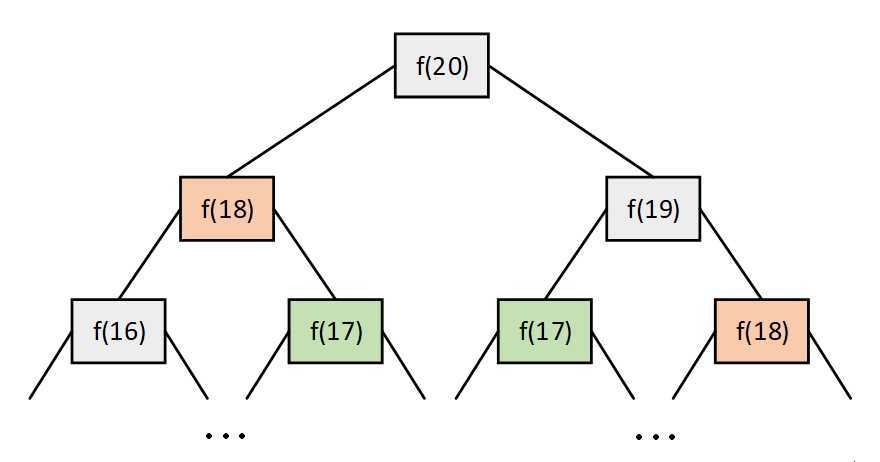
既然直接递归存在很大的冗余,那么我们可以通过备忘录来记录递归过程中子问题的解,备忘录可以是数组也可以是哈希表,求解子问题时先查看备忘录是否已经解决过,是则直接取解,否则求完解后记录上去,从而避免重复计算。代码如下:
int climbStairs (int n) {// 备忘录初始化 vector<int> memo(n + 1, 0); // 初始化最简情况 return helper(memo, n); } int helper(vector<int>& memo, int n) { if (n == 0 || n == 1) return 1; // 已经计算过 if (memo[n] != 0) return memo[n]; memo[n] = helper(memo, n - 1) + helper(memo, n - 2); return memo[n]; }
根据带备忘录的递归法,递归树如下图所示,我们可以发现,之前的大量冗余节点都被剪枝了,子问题的解被重复利用,省去了大量的时间消耗,时间复杂度降为O(n)。在该方法中,原问题通过递归逐步向下分解,直到f(1)和f(2)触底,然后逐层返回答案,我们称之为自顶向下。
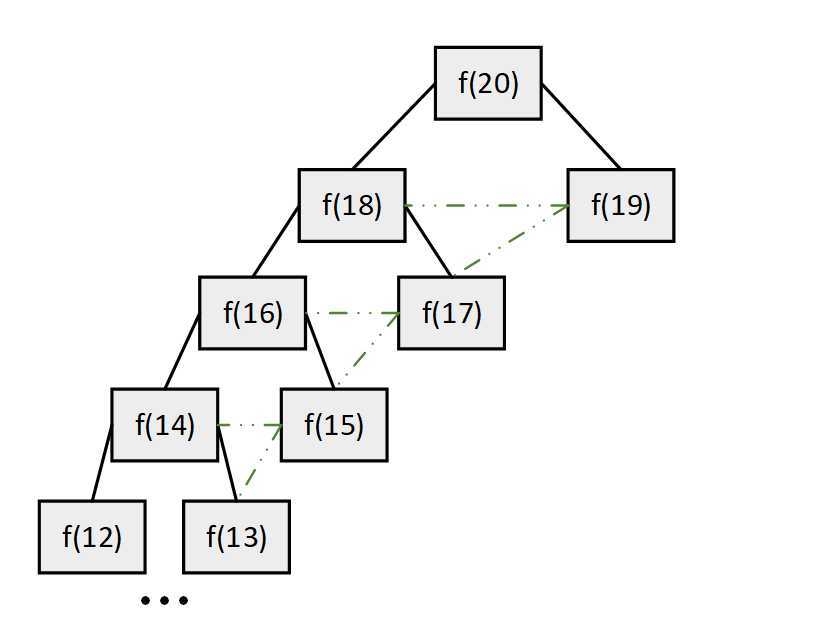
而动态规划则是自底向上的解法,即从问题规模最小的f(1)和f(2)开始往上递推,直到我们想要原问题,动态规划同样需要类似于备忘录的DP表来记录递推过程中子问题的解,从而解决冗余,时间复杂度与带备忘录的递归法相同。其中dp[i] = dp[i - 1] + dp[i - 2]称之为状态转移方程,用来描述状态转移即状态递推的具体形式。代码如下:
int climbStairs (int n) { vector<int> dp(n + 1, 0); dp[0] = dp[1] = 1; for (int i = 2; i <= n; i++) dp[i] = dp[i - 1] + dp[i - 2]; return dp[n]; }
通过以上的例子,我们详细分析了动态规划的问题特点以及基本思想,接下来就要介绍解决动态规划问题的四点步骤:
明确状态 -> 定义 dp 表 -> 明确选择 -> 明确 base case。
比如,在爬楼梯问题中,我们各步骤如下:
(1)明确状态:原问题和子问题变化的是楼层,所以状态为楼层。
(2)定义dp表:用数组dp[n]表示到达楼层n有dp(n)种方法。
(3)明确选择:对于每个状态,到达该状态可以选择上1个或者2个台阶。
(4)明确 base case:到达0层和1层只能有一种方法。
零钱兑换(LeetCode-322)
下面通过零钱兑换问题进一步了解动态规划问题解决步骤。
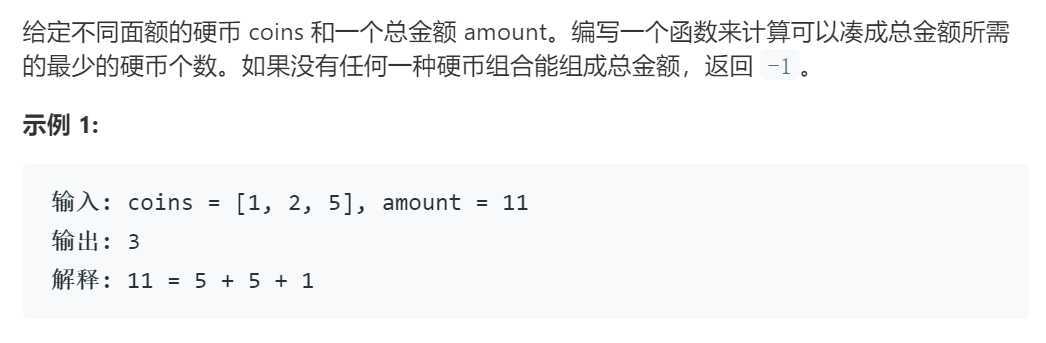
首先,这个问题是动态规划问题,因为它具有「最优子结构」,比如你想求amount = 11时的最少硬币数(原问题),如果你知道凑出amount = 10的最少硬币数(子问题),你只需要把子问题的答案加一(再选一枚面值为 1 的硬币)就是原问题的答案,因为硬币的数量是没有限制的,子问题之间没有相互制,是互相独立的。既然知道了这是个动态规划问题,就要思考如何列出正确的状态转移方程。
(1)明确状态:也就是原问题和子问题变化的变量,由于硬币数量无限,所以唯一的状态就是目标金额。
(2)定义dp表:用数组dp[n]表示当前的目标金额是n,至少需要dp(n)个硬币凑出该金额。
(3)确定选择并择优:也就是对于每个状态,可以做出什么选择改变当前状态。具体到这个问题,无论当的目标金额是多少,选择就是从面额列表coins中选择一个硬币,然后目标金额就会减少。
(4)最后明确 base case:显然目标金额为 0 时,所需硬币数量为 0;当目标金额小于 0 时,无解,返回 -1。
代码如下:
int coinChange(vector<int>& coins, int amount) { vector<int> dp(amount+1,amount+1); dp[0] = 0; for(int i=1;i<amount+1;i++) { for(int coin:coins) { if(i-coin>=0) { dp[i] = min(dp[i],dp[i-coin]+1); } } } return dp[amount]>amount?-1:dp[amount]; }
原文:https://www.cnblogs.com/BobPong/p/12685131.html