题目描述:
让我们定义d?n??为:d?n??=p?n+1??−p?n??,其中p?i??是第i个素数。显然有d?1??=1,且对于n>1有d?n??是偶数。“素数对猜想”认为“存在无穷多对相邻且差为2的素数”。
现给定任意正整数N(<),请计算不超过N的满足猜想的素数对的个数。
输入在一行给出正整数N。
在一行中输出不超过N的满足猜想的素数对的个数。
20
4
解题思路:
1、根据输入的数计算出所有的素数存储起来
2、遍历得到的素数数组,计算素数对,用两个指针来判断。
3、输出得到的素数对的个数
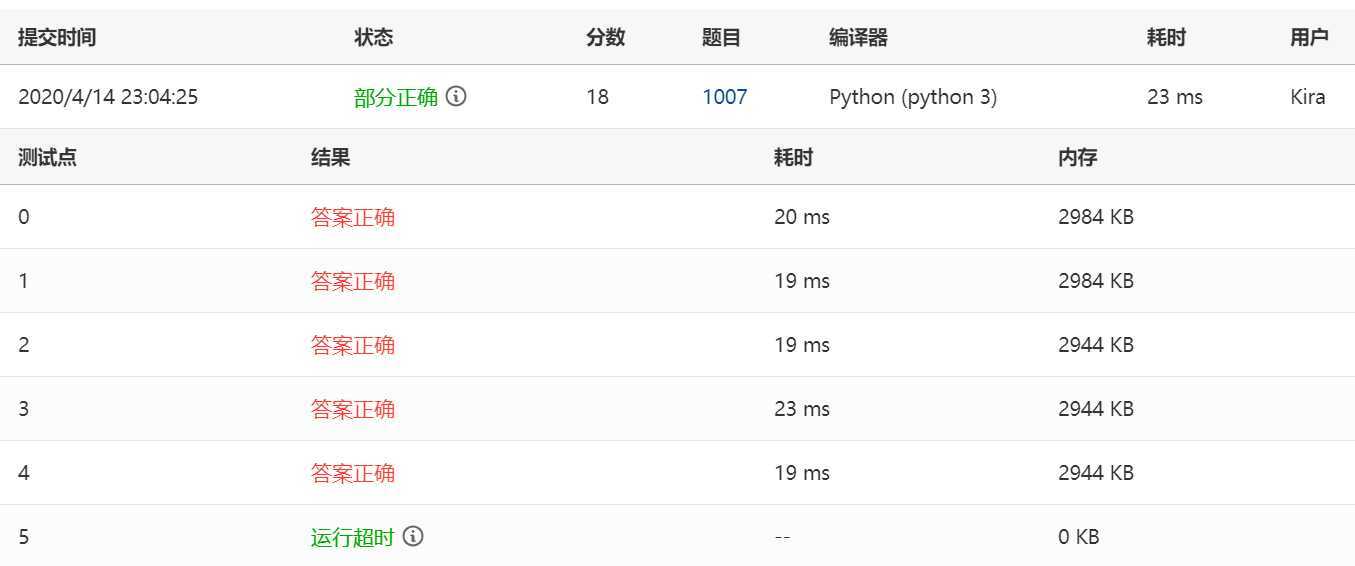
Python写的最后一个测试用例超时了,,???,,Python用的还不是特别熟练,等想到了更好的办法再更新
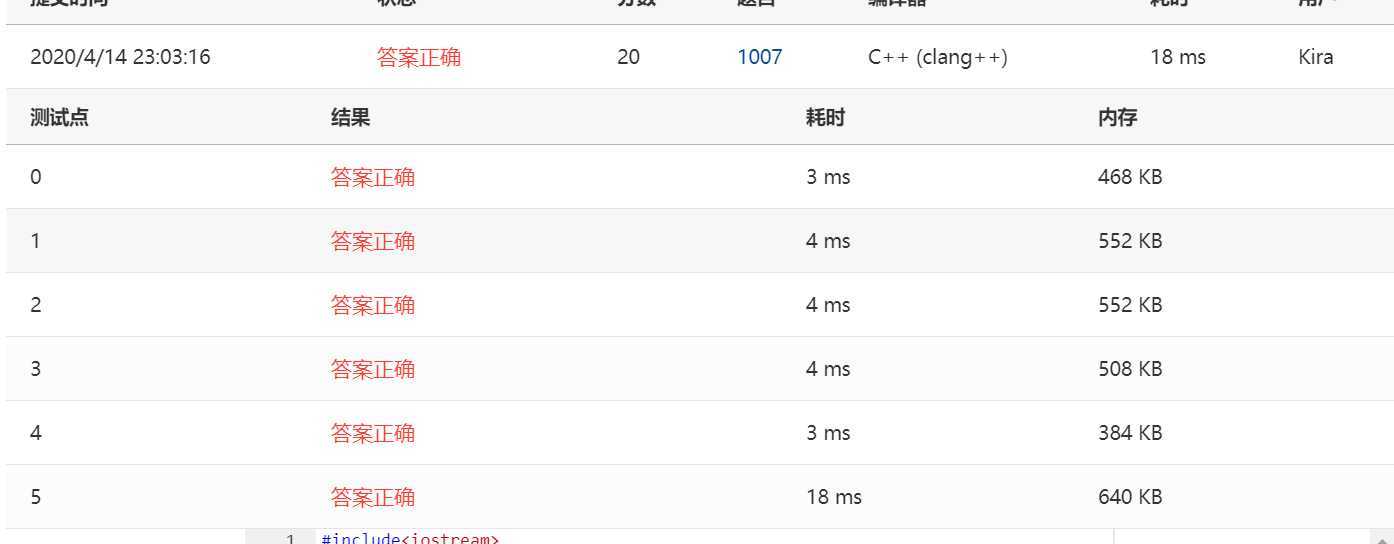
相同的思路C++就不会超时,,???,,两种代码都贴一下叭
Python:
import math as m def isPrime(num): if num <= 3: return num > 1 k = int(m.sqrt(num)) for nu in range(2, k+1): if num % nu == 0: return False return True N = int(input()) primelist = [] for i in range(2, N+1): if isPrime(i): primelist.append(i) count = 0 for x in range(0, len(primelist)): for y in range(x+1, len(primelist)): c = primelist[y] - primelist[x] if c > 2: break elif c == 2: count += 1 print(count)
C++
#include<iostream> #include<cmath> #include<vector> using namespace std; bool isprime ( int n ) { if ( n <= 3 ) { return n > 1; } // 求平方根,注意sqrt()的参数为 double 类型,这里要强制转换m的类型 int k = ( int )sqrt ( ( double )n ); int i; for ( i = 2; i <= k; i++ ) { if ( n % i == 0 ) { return false; } } // 如果完成所有循环,那么m为素数 return true; } vector<int> nums; int main () { int n; cin >> n; //计算2-n的全部素数,存储在vector中 for ( int i = 2; i <= n; i++ ) { if ( isprime ( i ) ) { //是素数,将数据放入数组中 nums.push_back ( i ); } } int count = 0;//素数对的计数器 for ( int i = 0; i < nums.size (); i++ ) { for (int j = i + 1; j < nums.size (); j++ ) { if ( nums [j] - nums [i] > 2 ) break; if ( nums [j] - nums [i] == 2 ) count++; } } printf ( "%d\n", count ); system ( "pause" ); return 0; }
原文:https://www.cnblogs.com/syq816/p/12702035.html