一:二分查找算法
性质:二分查找法实质上是不断地将有序数据集进行对半分割,并检查每个分区的中间元素
li = [1,2,3,4,5,6,7,8,9]
def find(li,item):
find = False
mid_index = len(li) // 2
first_index = 0
end_index = len(li)-1
while first_index <= end_index:
mid_index = (first_index + end_index) // 2
if li[mid_index] <= item:
first_index = mid_index + 1
elif li[mid_index] > item:
end_index = mid_index - 1
else:
find = True
break
return find
递归问题:
汉诺塔问题
汉诺塔问题不管在任何编程语言里都是经典问题,是采用递归算法的经典案例,该问题可以抽象如下:
一:3根圆柱A,B,C,其中A上面串了n个圆盘
二:这些圆盘从上到下是按从小到大顺序排列的,大的圆盘任何时刻不得位于小的圆盘上面
三:每次移动一个圆盘,最终实现将所有圆盘移动到C上
def hannota(n, fromit, throughit, toit):
if n == 1:
print(f‘{fromit} --> {toit}‘)
else:
hannota(n - 1, fromit, toit, throughit)
print(f‘{fromit} --> {toit}‘)
hannota(n - 1, throughit, fromit, toit)
hannota(3, ‘A‘, ‘B‘, ‘C‘)
#7次
‘‘‘
二:二叉树查找算法
二叉树的遍历:
广度优先遍历--》一层一层对节点进行遍历
深度优先遍历--》前序:根左右
中序:左根右
后序:左右根
特性:由其树状结构,对其做删除与插入是扰乱其结构的。所以之只能进行添加与查询。
作用:数据库、文件系统结构
时间复杂度:O(n)
‘‘‘
class Node(object):
‘‘‘创建节点‘‘‘
def __init__(self, item):
self.item = item
self.left = None
self.right = None
class Tree(object):
‘‘‘创造一颗树‘‘‘
def __init__(self):
self.root = None
def addNode(self, item):
node = Node(item)
‘‘‘如果书的根节点root是空,那么就创建第一个根节点root=node‘‘‘
if self.root == None:
self.root = node
return
cur = self.root # 根节点root创建了只有一个,所以赋值给cur
q = [cur] # 列表元素是遍历判断的节点
while q:
new_node = q.pop(0)
if new_node.left == None:
new_node.left = node
return
else:
q.append(new_node.left)
if new_node.right == None:
new_node.right = node
return
else:
q.append(new_node.right)
def travel(self):
cur = self.root
q = [cur]
while q:
nd = q.pop(0)
print(nd.item)
if nd.left:
q.append(nd.left)
elif nd.right:
q.append(nd.right)
‘‘‘深度优先遍历‘‘‘
def front(self,root): #前序:根左右
if root == None:
return
print(root.item)
self.front(root.left)
self.front(root.right)
def mid(self,root):#中序:左根右
if root == None:
return
self.mid(root.left)
print(root.item)
self.mid(root.right)
def back(self,root):
if root == None:#后序:左右根
return
self.back(root.left)
self.back(root.right)
print(root.item)
‘‘‘
下列五种查找算法,除顺序查找外,其他算法的思路基本相同:
先对数据按某种方法进行排序,然后使用相应的规则查找。
因此,搞清排序算法才是关键。
条件:无序或有序队列。
原理:按顺序比较每个元素,直到找到关键字为止。
时间复杂度:O(n)
条件:有序数组
原理:查找过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜素过程结束;
如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。
如果在某一步骤数组为空,则代表找不到。
这种搜索算法每一次比较都使搜索范围缩小一半。
时间复杂度:O(logn)
条件:先创建二叉排序树:
1. 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
2. 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
3. 它的左、右子树也分别为二叉排序树。
原理:
在二叉查找树b中查找x的过程为:
1. 若b是空树,则搜索失败,否则:
2. 若x等于b的根节点的数据域之值,则查找成功;否则:
3. 若x小于b的根节点的数据域之值,则搜索左子树;否则:
4. 查找右子树。
时间复杂度: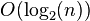
条件:先创建哈希表(散列表)
原理:根据键值方式(Key value)进行查找,通过散列函数,定位数据元素。
时间复杂度:几乎是O(1),取决于产生冲突的多少。
原理:将n个数据元素"按块有序"划分为m块(m ≤ n)。
每一块中的结点不必有序,但块与块之间必须"按块有序";即第1块中任一元素的关键字都必须小于第2块中任一元素的关键字;
而第2块中任一元素又都必须小于第3块中的任一元素,……。
然后使用二分查找及顺序查找。
原文:https://www.cnblogs.com/cou1d/p/12718740.html