线性模型笔记-20200416

线性模型是机器学习中应用最广泛的模型，利用样本特征的线性组合来进行预测，对于给定的一个d维样本[x1,x2,...,xd]^T,其线性组合函数为

f(x;w)=w1*x1+w2*x2+...+wd*xd+b=w^T*x+b

其中w=[w1,w2,...,wd]^T是d维的权重向量，b为偏置。

分类问题中，输出目标y是一些离散的标签，而f(x;w)是连续的实数，因此需要引入一个非线性的决策函数（Decision Function)

y=g(f(x;w))

f(x;w)是支撑决策的依据，称为判别函数（Discriminant function）, g-非线性决策函数，对于二分类问题，可以使用符号函数Sign Function.

一个线性分类模型（Linear Classification Model）或者线性分类器（Linear Classifier）是由一个或者多个线性判别函数f(x;w)和非线性决策函数组成。

所谓线性分类模型就是指决策边界是线性超平面。在特征空间中，决策平面和权重向量正交，特征空间中每个样本点到决策平面的距离为

γ=f(x;w)/|| w ||

给定具有N个样本的训练集D={x⁽ⁿ⁾,y⁽ⁿ⁾}_n=1:N,其中y∈{+1，-1}，线性模型试图学习到参数w*, 使得对于每个样本f(x;w)>0 if y>0;f(x,w)<0 if y<0.

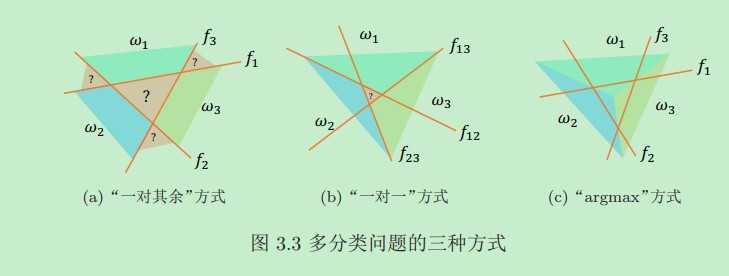
对于类别大于2的数据集，此时分类问题变成多分类问题，常见的多分类策略可以分为以下三种：

1. “一对其余”方式：把多分类问题转换为C个一对其余的二分类问题，共需要C个判别函数；
2. “一对一”方式：把多分类问题转换为C*(C-1)/2个一对一的二分类问题
3. “argmax”方式：一种改进的一对其余的方式，共需要C个判别函数，如果对于类别c, 对于其他的类别满足fc(x;wc)>f(not c)(x;w(not c)),那么该类属于c类
4. 总结：考虑到样本特征在空间分布存在部分重合的情况，这个时候“一对其余”、“一对一”都会不适用，argmax是最合理的方式。

Logistic回归

为了解决连续的线性函数不适合分类的问题，引入非线性函数g来预测类别标签的后验概率p(y=1|x)=g(f(x;w)),g通常称为激活函数，其作用是把线性函数的值域从实数区间挤压到（0，1）之间，可以用来表示概率。Logistic回归使用交叉熵损失函数，利用梯度下降法进行参数学习。

标准版logistic函数

σ(x)=1/(1+exp(x))

标准版Logistic函数在机器学习中使用非常广泛，用来将一个实数空间映射到（0，1）区间。

Softmax回归

softmax回归是Logistic回归在多分类问题上的推广。

Softmax函数：

zk=softmax(xk)=exp(xk)/sum(exp(xi))

可以将K个标量x1,x2,...xk转换为一个分部z1,z2,...zk,满足zk∈（0，1）并且sum(zk)=1.

感知器

感知器是一种广泛使用的线性分类器，可谓是最简单的人工神经网络，只有一个神经元

支持向量机，其找到的分割超平面具有更好的鲁棒性，在很多任务上具有很强的优势。给定一个二分类数据集D={x⁽ⁿ⁾,y⁽ⁿ⁾}n=1,2,...N,y∈（+1，-1），如果两类样本在当前空间或者投影到其他特征空间以后可分，即存在一个超平面

wT*x+b=0

那么，对每个样本都有y^k(W^T*x^k+b)>0.数据集D中每个样本到分割超平面的距离为：

γ(n)=||  W^T*x(n)+b || / || w ||

支持向量机的目标就是找到一个超平面使得样本到分割超平面的最小距离最大。对于一个线性可分的数据集，其分割超平面有很多个，但是间隔最大的超平面只有一个，因此相比其他线性分类模型，支持向量机可以取得更优的分类效果，并且鲁棒性更好。支持向量机的主优化问题为凸优化问题，可以使用凸优化问题得到全局最优解，学习效率更高，支持向量机的决策函数只依赖于支持向量，与训练样本总数无关，分类速度更快。

支持向量机还有一个重要的优点是可以使用核函数将样本从原始特征空间映射到更高维的空间，从而解决原始特征空间中线性不可分问题。

线性模型笔记-20200416

原文：https://www.cnblogs.com/tpzang/p/12714227.html