题面

测试要求 Bob 尽可能快地切断 n 根绳子。

所有绳子的端点两两不同，所以共有 2n 个端点。这些端点被捆在一个圆上，等距离分布。我们把这些端点按顺时针方向编号为 1 到 2n。

Bob 每次切割的轨迹是一条直线，可以将所有与这条直线相交的绳子切断，他想知道至少多少次可以切断所有的绳子。

\(n<=2*10^5\)

传送门

题解

先破环成链

我们可以想到，对于原本环上存在的一条线段，我们可以标记一下它两端点在链上的位置
而一条直线穿过了此线段，则说明此线段两端点的弧中一定存在一个Bod用太极剑划出的直线的端点

所以我们只要保证：

圆上两个标记相同的点之间一定要有一个断点

考虑如何贪心:

对于两个标记相同的点，肯定将断点设在靠右的端点上会更优，因为这样能够断开更多其他标记相同的点

此外我们还需要找到最开始的断点

(这图我盗的，图片作者抱歉)

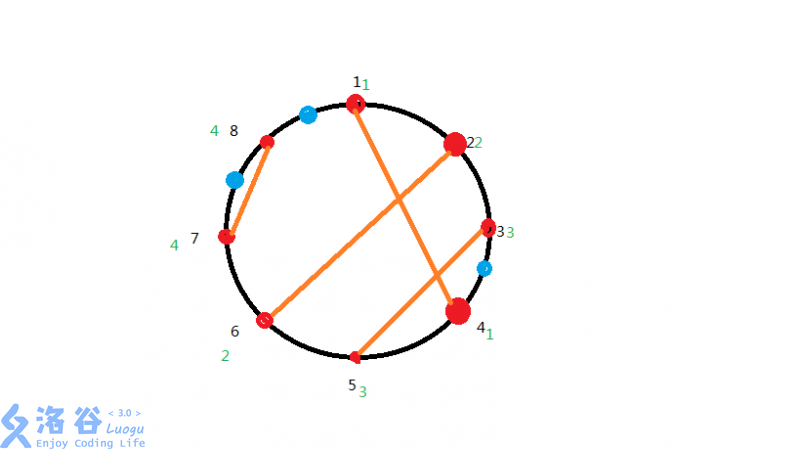
比如上图中，有三个断点，却只需要一条直线
仔细想想就能知道断点枚举的顺序影响了最终结果

因为端点之间必定有端点，所以较短的端点距离会比较长的端点距离更好枚举作为断点

所以我们直接找到最小的端点距离，枚举初始断点

最后

我们来想想看它的复杂度，设最小的端点距为d
所以之后每个端点之间必定会大于间隙d,而断点的选择会是下一个还未被断开的线段的靠右的端点，所以关于找到下一个断点，可以直接在此位置+d，再一一向后枚举
所以总复杂度为：
\(O（d（枚举初始节点）*（2*n/d）（对于每个初始节点向后递推位置））\)

代码

#include<bits/stdc++.h>
using namespace std;
#define re register
#define in inline
#define ll long long
#define get getchar()
in int read()
{
    int t=0,x=1;char ch=get;
    while((ch<‘0‘||ch>‘9‘)&&ch!=‘-‘)ch=get;
    if(ch==‘-‘)x=-1,ch=get;
    while(ch<=‘9‘&&ch>=‘0‘)t=t*10+ch-‘0‘,ch=get;
    return x*t;
}
const int _=8e5+5;
int n;
struct edge{
	int l,r;
}a[_];
int to[_];
in int dis(int x,int y)
{
	return min(y-x,2*n-y+x);
}
int main()
{
    n=read();
    int minx=0x3f3f3f3f,xx;
    for(re int i=1;i<=n;i++)
    {
    	a[i].l=read(),a[i].r=read();
	if(a[i].l>a[i].r) swap(a[i].l,a[i].r);
	to[a[i].r]=a[i].l;
	to[a[i].l+2*n]=a[i].r;
	to[a[i].r+2*n]=a[i].l+2*n;//倍长区间，标记每个区间右端点对应的左端点
	if(minx>dis(a[i].l,a[i].r)){
    	    minx=dis(a[i].l,a[i].r);
	    xx=i;	//记录最小距离的区间
	}
    }
    int st,en,ans=0;
    if(a[xx].r-a[xx].l==minx)
	st=a[xx].l,en=a[xx].r;
    else en=a[xx].l+2*n,st=a[xx].r; //标记最小距离区间起始点与结束点
    int len=dis(a[xx].l,a[xx].r);
    for(re int i=st;i<=en;i++)
    {
    	int last=i;ans=0;//last记录上一个断点
	for(re int j=i+len;j<i+2*n;j++)
    	    if(to[j]>last) ans++,last=j,j+=len; //判断条件是如果当前区间不会被上一个断点断开，则新开一个断点
    }
    cout<<(ans)/2+1<<endl;
    return 0;
}

LuoguP4704 太极剑

原文：https://www.cnblogs.com/yzhx/p/12723430.html