1.暴力法
思路:
循环遍历每一个子串,对每个子串进行判断,判断的方法为翻转子串和原子串进行对比,如果一致则为回文子串。
例如:
abcb

可以看出最长的回文子串为bcb
代码:
class Solution: def longestPalindrome(self, s: str) -> str: length = len(s) if length<=1: return s max_length = 1 begin = 0 end = 0 for first in range(0,length): for last in range(first+1,length): now_s = s[first:last+1] if now_s == now_s[::-1] and (last-first+1)>max_length: begin = first end = last+1 max_length = last - first +1 return s[begin:end]
2.动态规划法
思路:
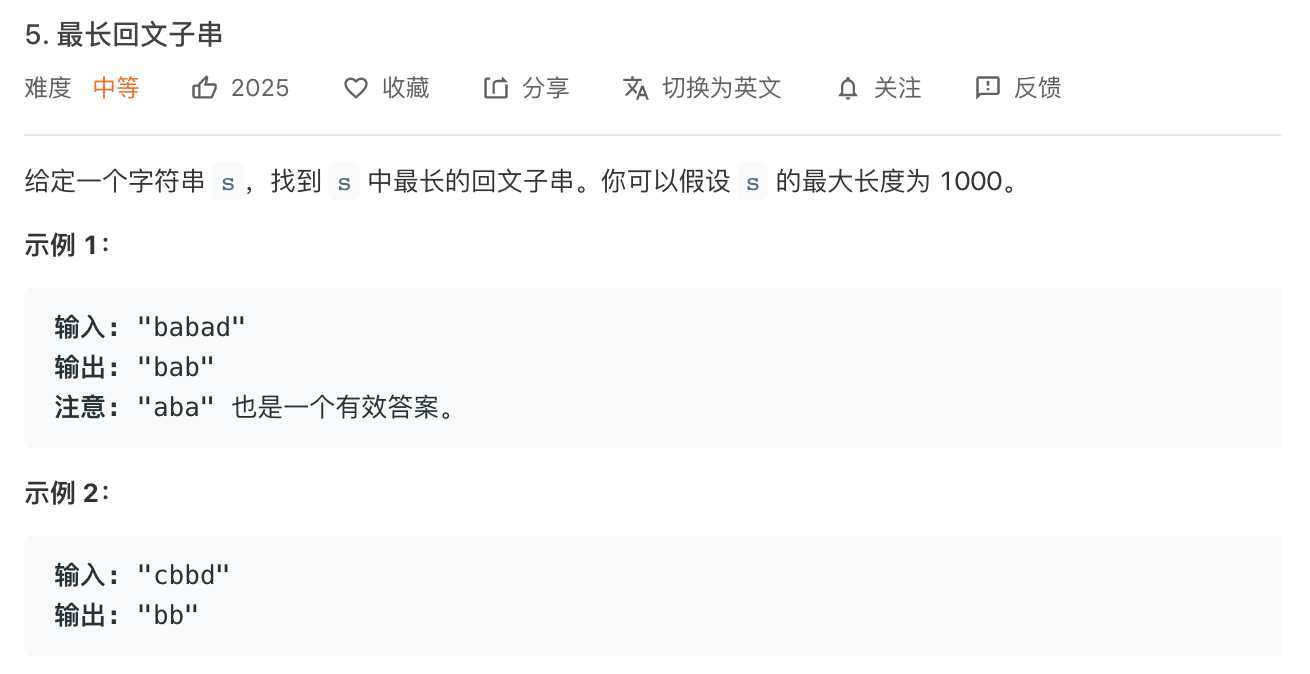
用i和j代表数组中相应位置元素,创建dp[i][j]二为数组,二维数组代表从i到j是否为回文子串。这里可以知道如果dp[i+1][i-1]为回文子串并且s[i]==s[j],则i到j的子串必为回文子串即dp[i][j]=1。
例如:
abcbad
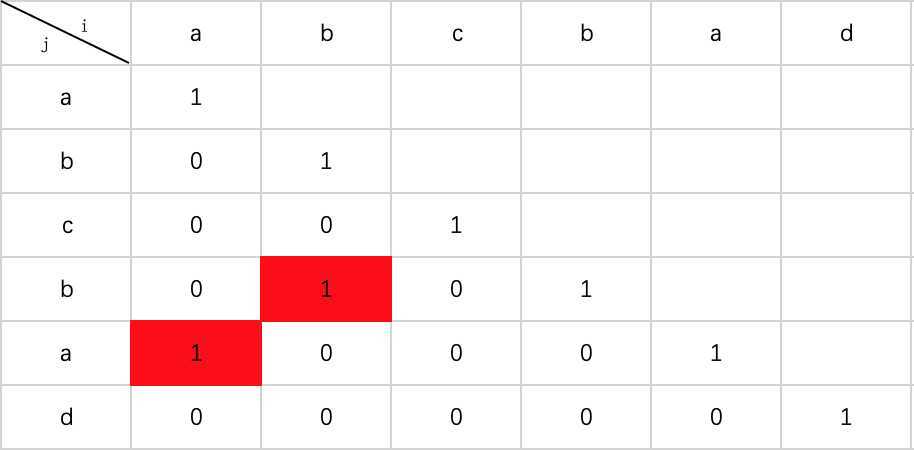
当i=0,j=4时,可以看出s[0]==s[4],并且由于dp[1][3]=1,所以dp[0][4]=1
代码:
class Solution: def longestPalindrome(self, s: str) -> str: length = len(s) if length<=1: return s dp=[[0]*length for _ in range(length)] max_length = 0 begin = 0 end = 0 for i in range(length): for j in range(i,-1,-1): if s[i]==s[j] and (i-j<2 or dp[i-1][j+1]): dp[i][j]=1 if max_length < i-j+1: max_length = i-j+1 begin = j end = i+1 return s[begin:end]
3.中心扩散法
思路:
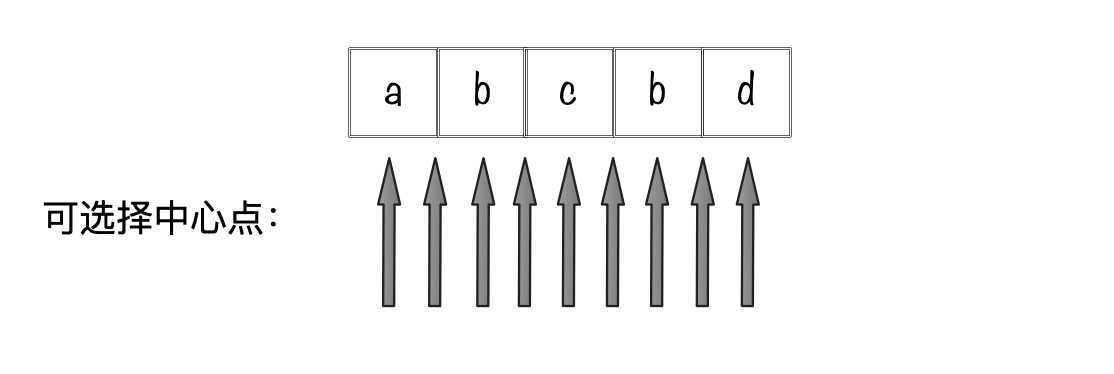
找一个中心点向两边扩散,如果中心点的左边等于右边,则对应子串为回文串。这里需要注意的是长度为n的字符串,有2n-1个中心点,所以选择中心点的时候要分情况讨论奇偶性。
例如:
abcbd
代码:
class Solution: def longestPalindrome(self, s: str) -> str: length = len(s) if length<=1: return s self.res = s[0] def findMaxlengthSubStr(i,j): while i>=0 and j<length and s[i]==s[j]: i-=1 j+=1 if len(self.res) < j - i -1: self.res = s[i+1:j] for i in range(length): findMaxlengthSubStr(i,i) findMaxlengthSubStr(i,i+1) return self.res
4.马拉车(manacher)法
思路:
在使用中心扩展法时,我们在选中心点时需要考虑奇偶性,同时在选择每个中心点时都要进行扩散。manacher法实际上是对中心扩展法的一个改进,先对字符串添加字符使新的字符串长度为奇数,同时充分利用所找到回文串的对称性原则,减少后续中心点一些不必要的扩散。
分析:
ababaac
1.先对字符串添加字符使其为奇数,原理是对首尾和每个字符间隔地方加入同样的字符,然后在首尾添加起始和截止不同的字符。比如

2.接下来需要记录每个中心点的回文半径,即以这个中心点为圆心,它能找到的最长回文串长度的1/2
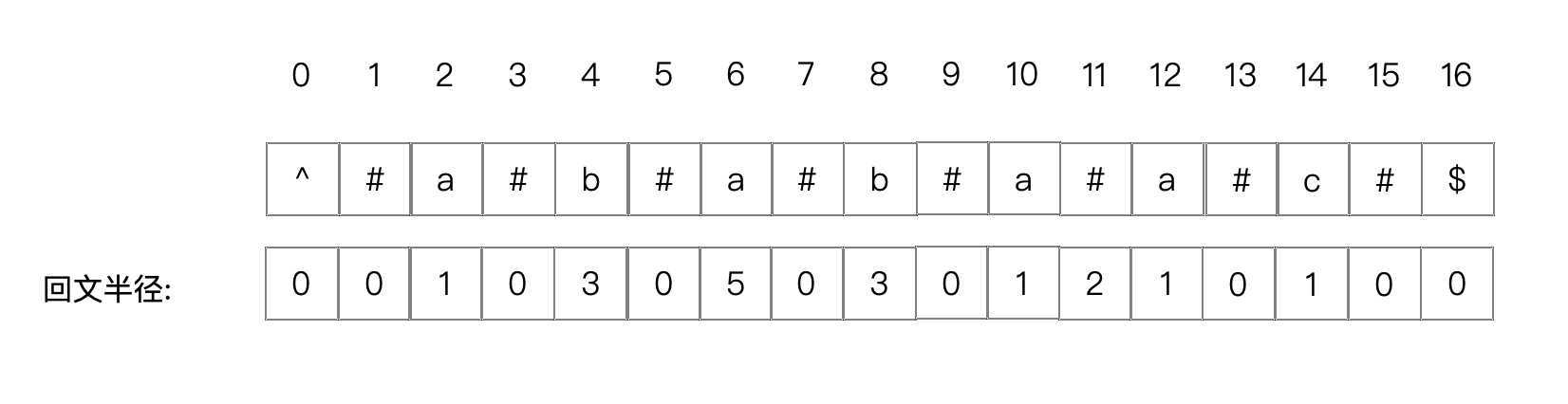
3.找到回文半径最大的那个数,即下标为6的r(a) = 5,也就是说原字符串回文串长度为5。这里a的下标减去a的回文半径,然后除二即为原字符串回文子串起始位置,即(6-5)/2=0。再以0为起点取到5-1=4的位置的子串即为所要最大回文子串即ababa。
接下来需要研究如何充分利用回文串对称性减少不必要扩散来求得回文半径
分析:
一个回文串从中心开始,左右字符具有对称性,那么左右字符所对应的回文半径是否相同呢。分情况讨论:
(以C代表中心点的下标,R代表中心点右边回文半径所指位置,I为要获得中心半径的下标,M为在回文串中I对称点的下标)
1. I 加上M的回文半径L,如果小于R,则右边字符的回文半径与左边相等
即 I + L[M] < R ,则 L(I) = L(M)
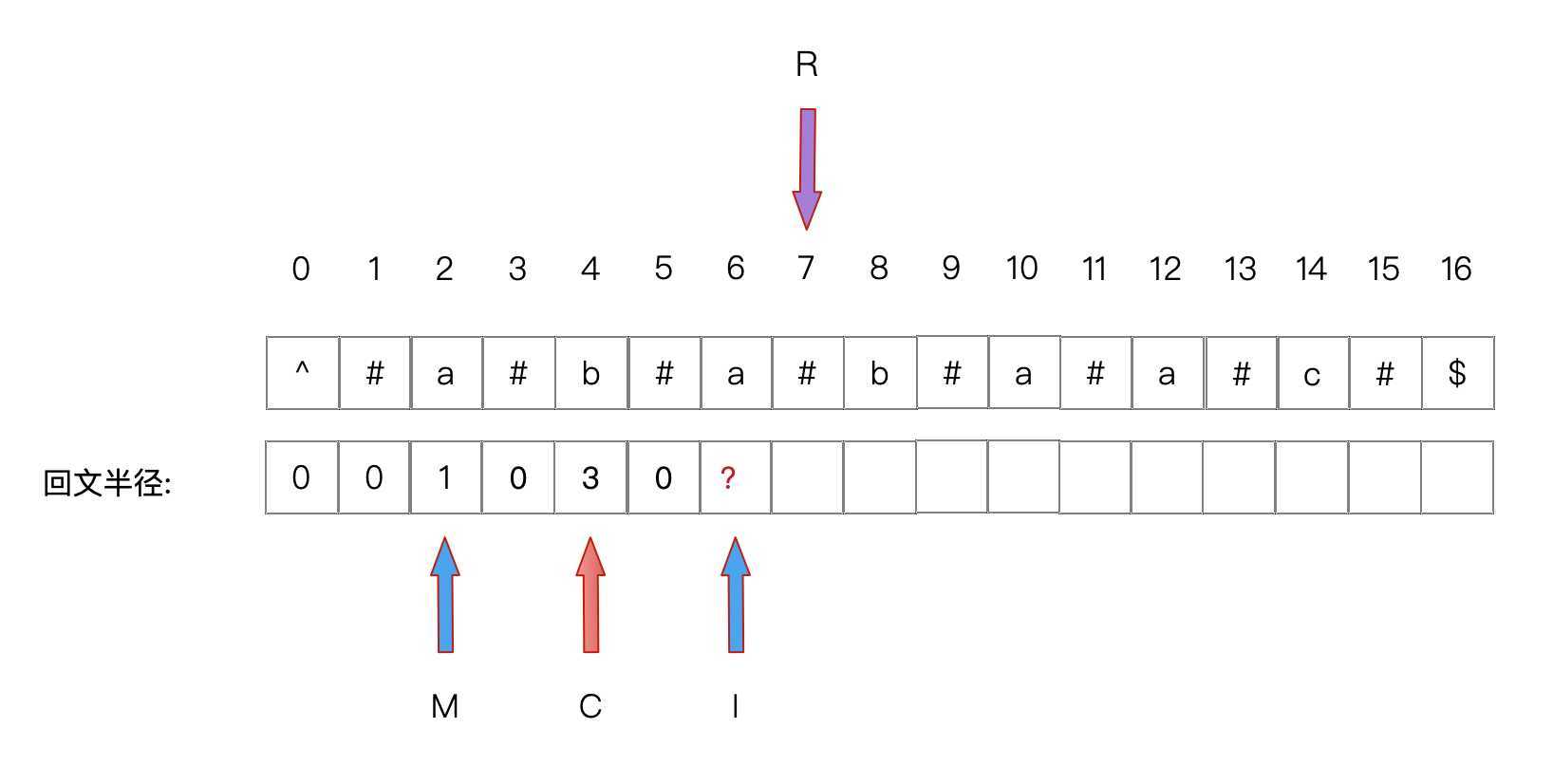
2. I 加上M的回文半径L,如果大于R,则以 I 为中心从 I+L(M)-R开始进行扩散
查找 I 的回文半径,查找到后更新中心点C为I,同时更新R
即 I + L[M] > R ,特定位置扩散找L(I),C = I ,R = I+L(I)
3. I == R,则以 I 为中心扩散查找回文半径,然后更新C为I,更新R
即 I = R ,扩散找I ,C = I ,R = I + L(I)
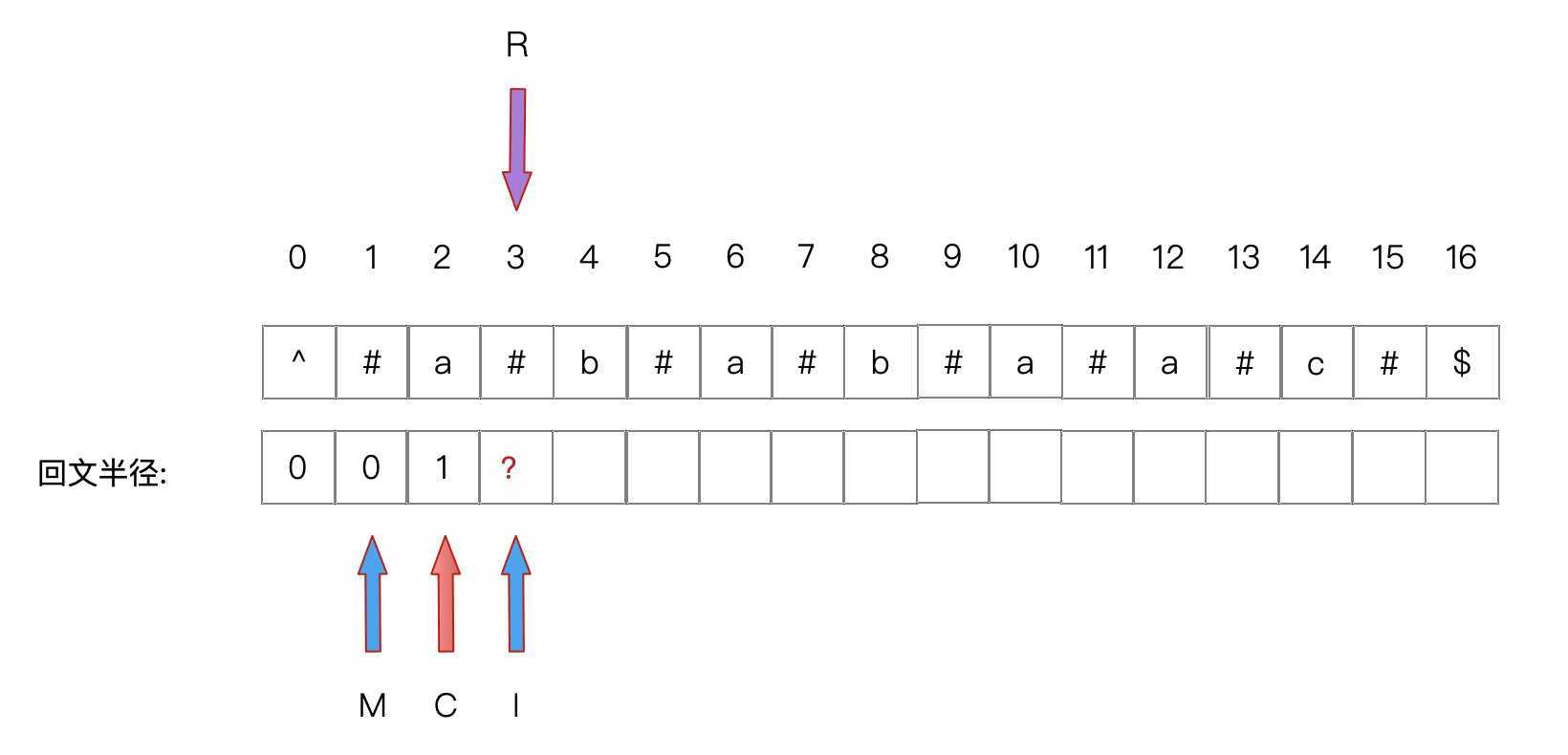
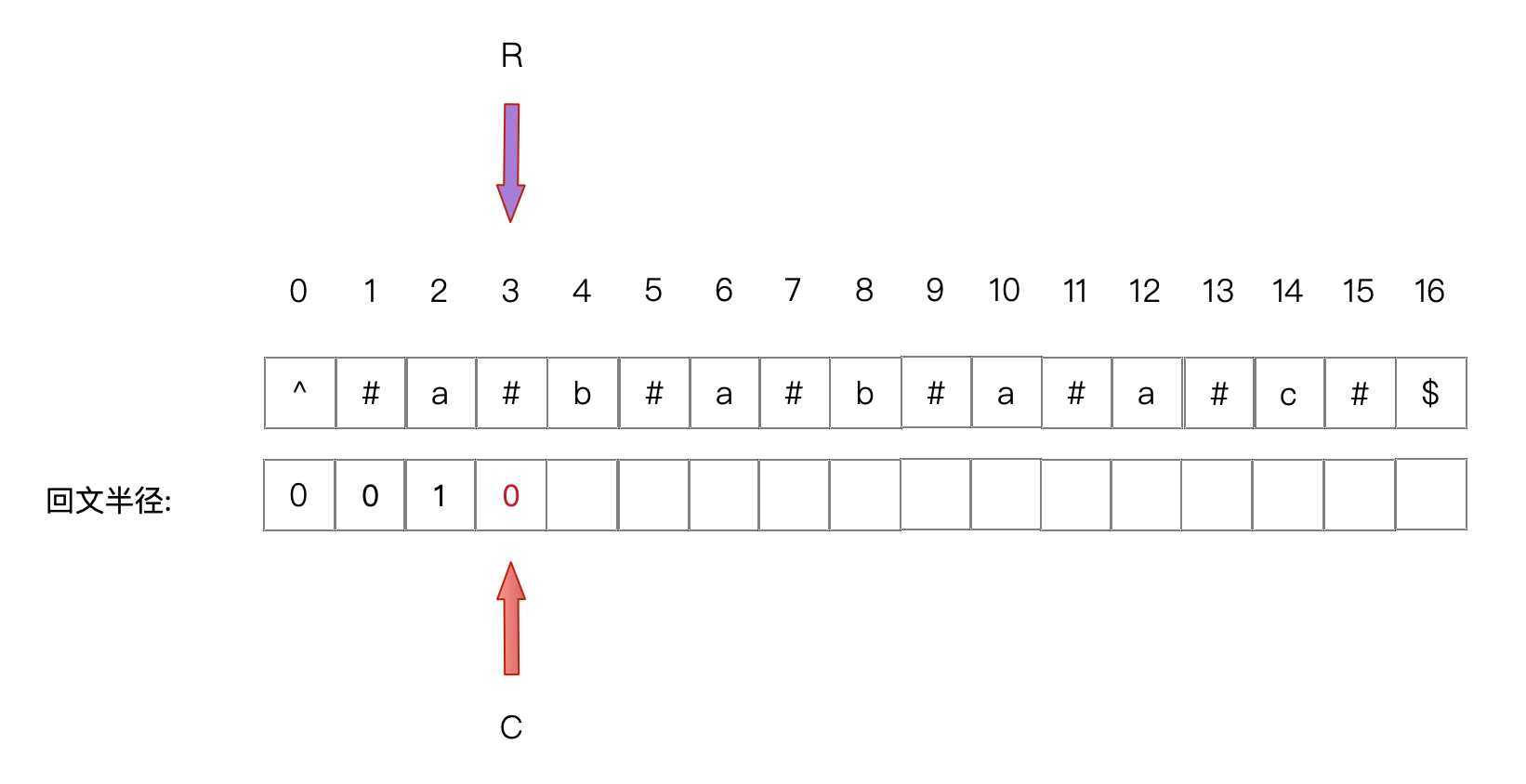
此时 I = R ,对 I 进行中心扩散,得L(I)=0,同时将C更新到I,R更新
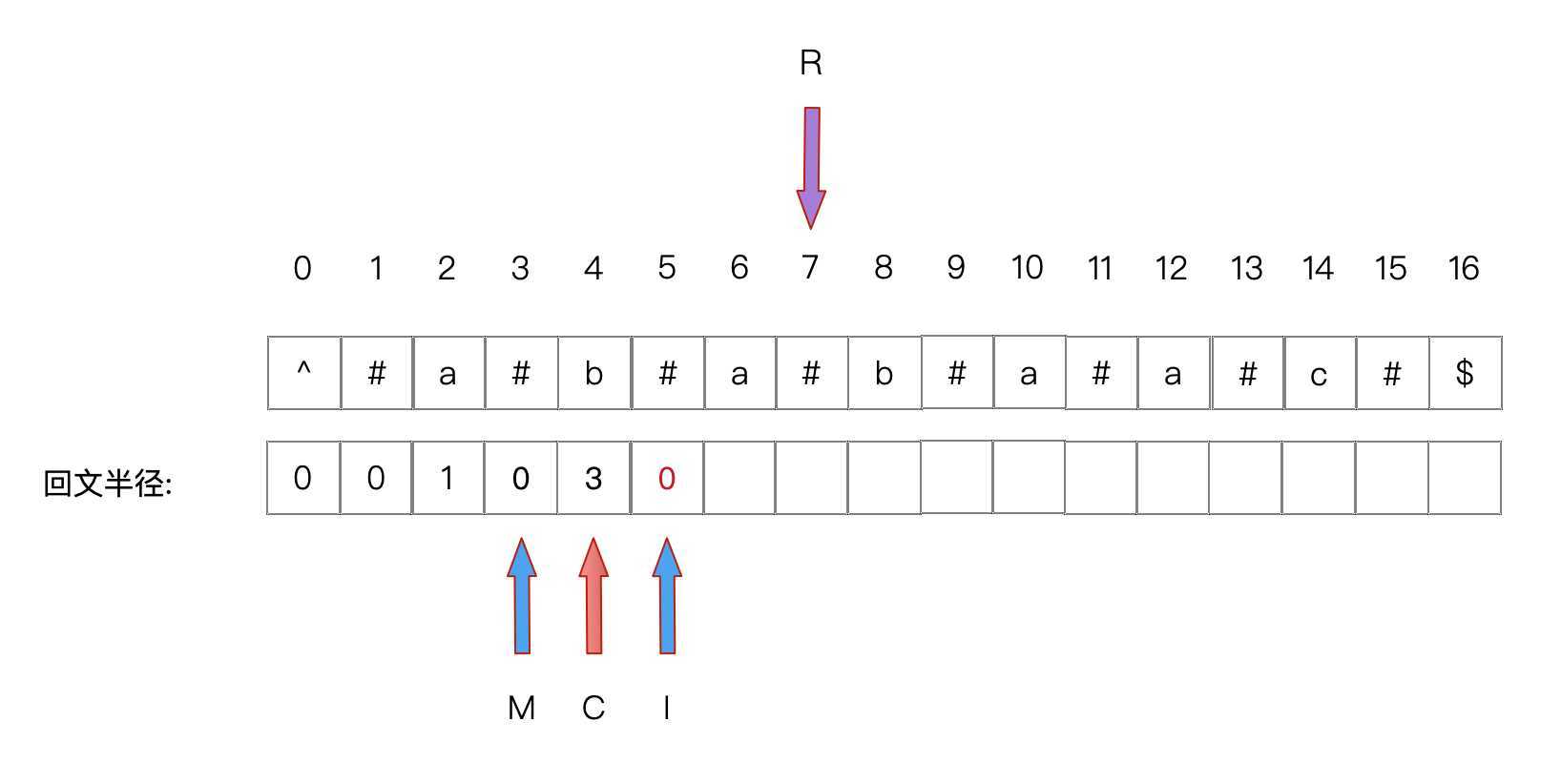
此时I+L(M)<R,所以L(I)=L(M)=0,继续下一步操作
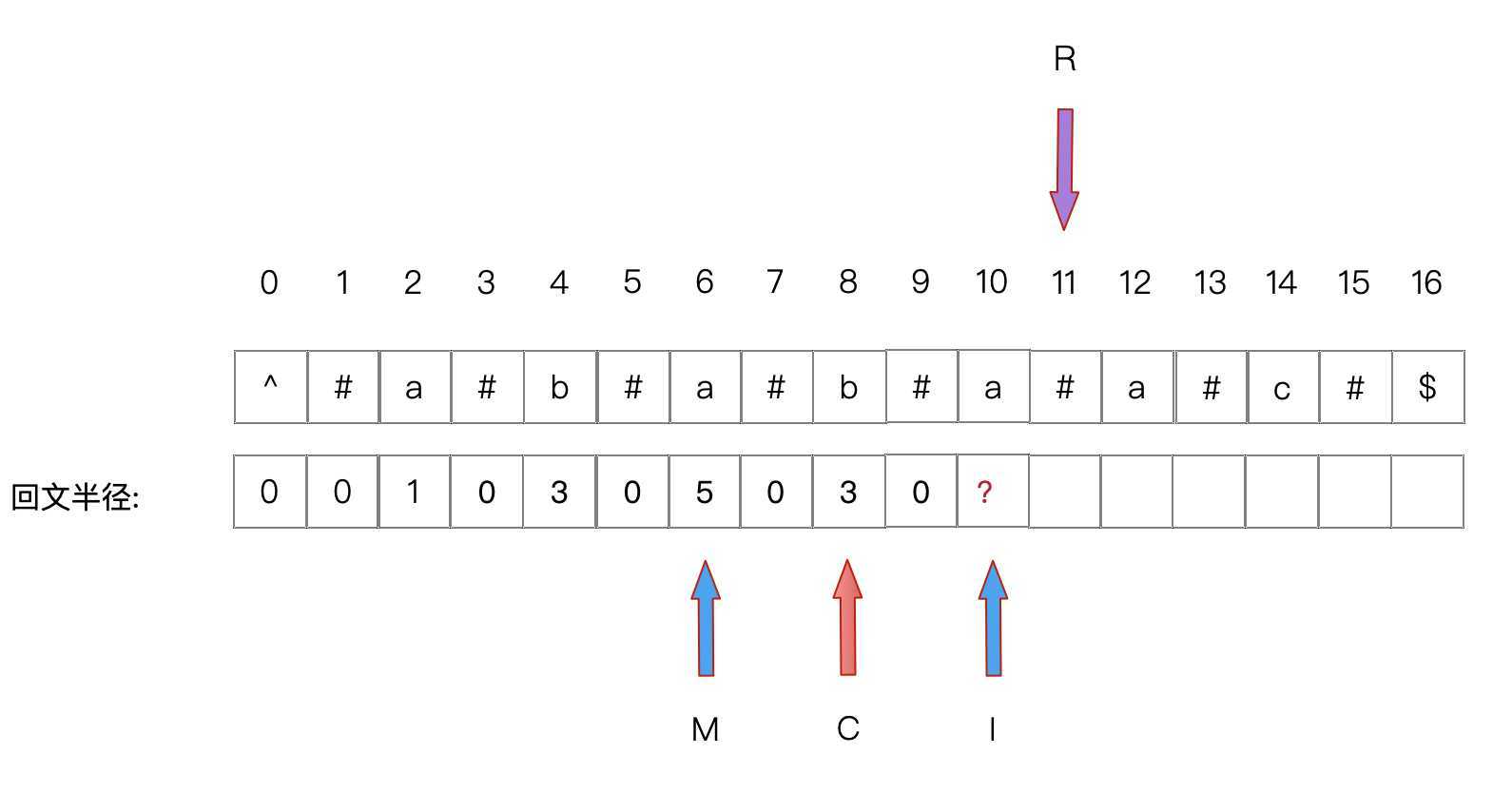
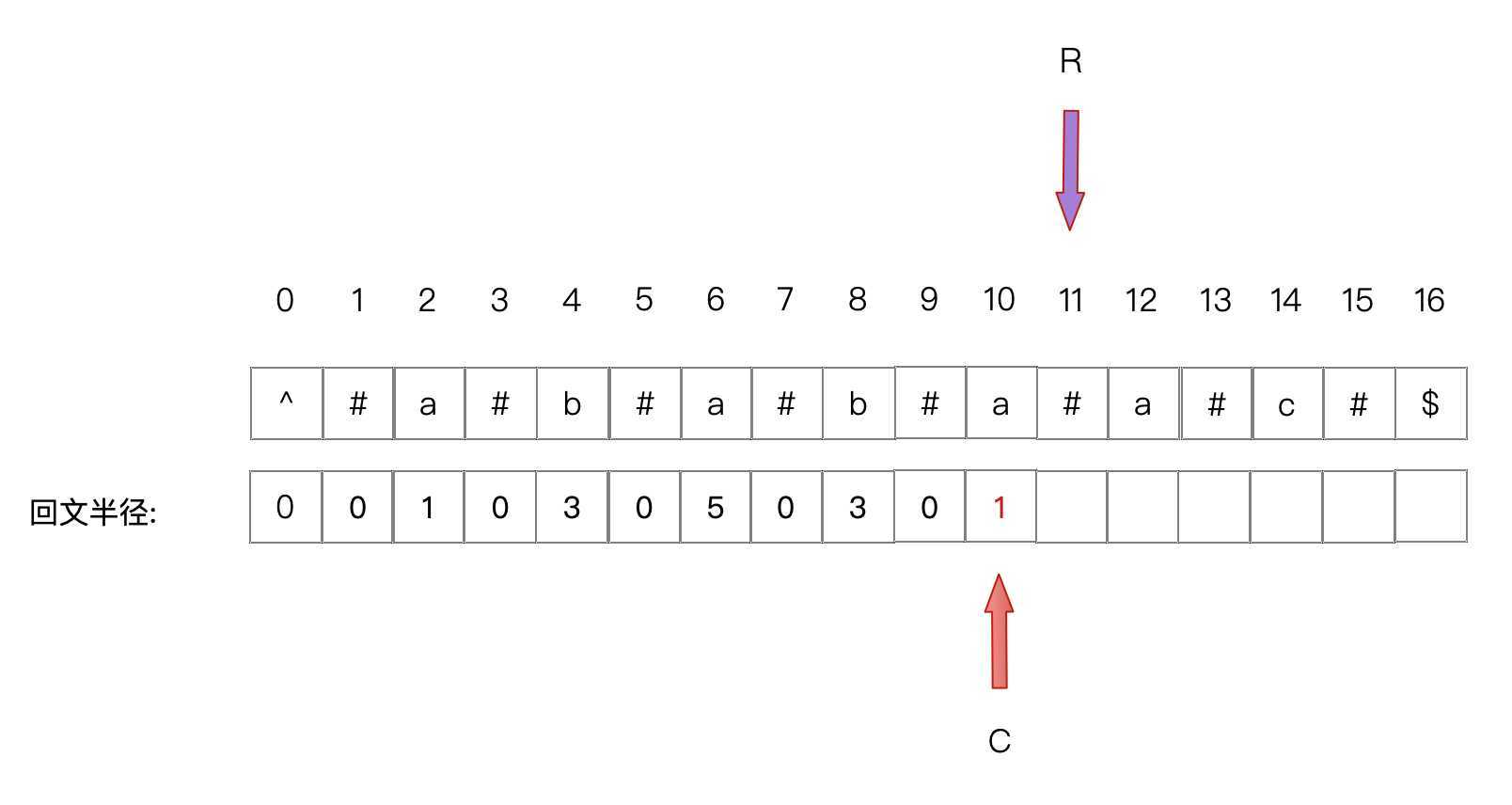
此时 I + L(M) > R,所以扩散找 I 的回文半径,找到后更新C和R
代码:
def longestPalindrome(self, s: str) -> str: new_s = "^#"+"#".join(s)+"#$" length = len(new_s) C = 0 R = 0 P = [0]*length max_length = 0 max_index = 0 for i in range(1,length-1): i_mirror = 2*C -i if R>i: P[i] = min(R-i,P[i_mirror]) while new_s[i+1+P[i]] == new_s[i-1-P[i]]: P[i] = P[i] +1 if i+P[i]>R: C = i R = i+P[i] for j in range(len(P)): if P[j] > max_length: max_length = P[j] max_index = j start = int((max_index-max_length)/2) return s[start:start+max_length]
原文:https://www.cnblogs.com/nilhxzcode/p/12723646.html