一、编写SearchBST(T, key)与InsertBST(T, key)的伪代码,并实现;
/*查找伪代码*/ SearchBST(T, key) { if (T为空 || T == key) { return T; } if (T > key) { search(T->lchild, key);//在左子树中查找 } else { search(T->rchild, key);//在右子树中查找 } } /*查找代码实现*/ BSTNode SearchBST(BSTNode* T, int key) { if (T == NULL || T->data == key) { return T; } if (key < T->data) { return SearchBST(T->lchild, key); } else { return SearchBST(T->rchild, key); } } /*插入伪代码*/ InsertBST(T, key) { if (T为空) { T = new Node; T = key; T->lchild = NULL; T->rchild = NULL;//初始化T,左右子树指向空 } else if (key==T) return 0;//T中已存在key else if (key < T) { return InsertBST(T->lchild, key);//插入到左子树 } else return InsertBST(T->rchild, key);//插入到右子树 } /*插入代码实现*/ BSTree* InsertBST(BSTree* T, int key) { if (T == NULL) { T = new BSTNode; T->data = key; T->lchild = NULL; T->rchild = NULL; } else if (key == T) return 0;//T中已存在key else if (key < T) { return InsertBST(T->lchild, key);//插入到左子树 } else return InsertBST(T->rchild, key);//插入到右子树 }
二、编写CreateBST(T)的伪代码实现从控制台输入创建BST树。最后使用代码实现。使用“50 30 80 20 40 90 10 25 35 85 23 88”创建BST,并中序输出该BST
CreateBST(T)的伪代码和代码
/*伪代码*/ CreateBST(T) { 初始化T为空树 for(i < n){ cin >> 值; InsertBST(值); } return T;//返回建立的BST的根指针 } /*代码*/ BSTree* CreateBST(int a[],int n) { BSTree*bt= NULL; for (int i = 0; i < n; i++) { cin >> a[i]; InsertBST(bt,a[i]); } return bt; }
使用“50 30 80 20 40 90 10 25 35 85 23 88”创建BST,并中序输出该BST
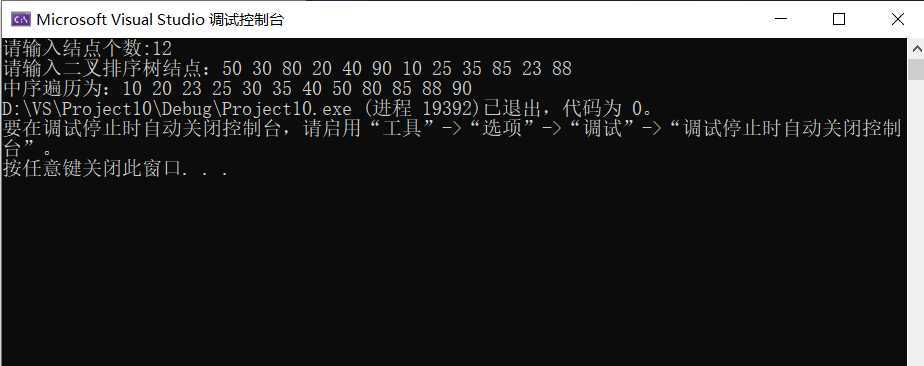
全部代码
#include<iostream> using namespace std; typedef struct BSTNode { int data; struct BSTNode* lchild; struct BSTNode* rchild; }BSTree; bool InsertBST(BSTree*& bt, int key); BSTree* CreateBST(int a[], int n); void InOrder(BSTree* bt); int main() { BSTree T; int a[50]; cout << "请输入结点个数:"; int n; cin >> n; cout << "请输入二叉排序树结点:"; BSTree* root = CreateBST(a, n); cout << "中序遍历为:"; InOrder(root); return 0; } /*代码*/ BSTree* CreateBST(int a[],int n) { BSTree*bt= NULL; for (int i = 0; i < n; i++) { cin >> a[i]; InsertBST(bt,a[i]); } return bt; } bool InsertBST(BSTree* &T, int key) { if (T == NULL) { T = new BSTNode; T->data = key; T->lchild = NULL; T->rchild = NULL; } else if (key == T->data) return false;//T中已存在key else if (key < T->data) { return InsertBST(T->lchild, key);//插入到左子树 } else { return InsertBST(T->rchild, key);//插入到右子树 } } void InOrder(BSTree* T) { if (T != NULL) { InOrder(T->lchild); printf("%d ", T->data); InOrder(T->rchild); } }
三、编写DeleteBST(T, key)的伪代码实现从T中删除关键字key。如果无法编写出来,请写出在BST中删除关键字key所需注意的事项。
注意事项及要点:
首先要判断要删除的关键字key所在结点位置
1、若是在叶子结点,则直接删除该结点。
2、若key所在结点只有一个子树,则删去key所在结点,用其子树代替该结点。
3、若key所在结点同时有左右子树,用其前驱结点代替T结点,再删去前驱结点,前驱是左子树中最大的结点。或者用key的后继结点代替T结点,后继是右子树最小的结点。
伪代码:
DeleteBST(T, key) { if (T为空) return 0;//空树删除失败 else { if (key<T->data) {//删除在左子树为key的结点 return DeleteBST(T->lchild, key); } else if (key>T->data) {//删除在右子树为key的结点 return DeleteBST(T->rchild, key); } else { if (T->lchild为空) {//只有右子树 p = T; T = T->rchild; free(p); } else if (T->rchild为空) {//只有左子树 p = T; T = T->lchild; free(p); } else {//左右子树都有 Delete(T, T->lchild);//调用Delete函数删除结点T } } } }
原文:https://www.cnblogs.com/hlq0710/p/12733687.html