判断一个数字是不是3的幂【python】

目录

• 解题方法
• 解题方法之间的比较
• 结论

解题方法

Given an integer, write a function to determine if it is a power of three.

判断一个整数是否是3 的幂。

Answer1: （我的答案）

思路：

1. 判断是否为3的倍数

2. 在3的倍数中，判断是否为3的幂

3. 循环中，只要有余数就不是3的幂，并且跳出循环

4. 剩下的数就是3的幂

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        out = None
        if n == 1:
            out = True
        elif n%3 != 0:
            out = False
        else:
            while n > 1:
                y = n%3
                if y != 0: 
                    out = False
                    break
                n = n/3
                out = True
        return out
   

Solution

Approach 1: Loop Iteration(循环)

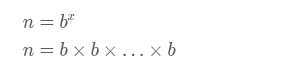
def isPowerOfThree(n):
    if n < 1:
        return False
    while n%3 == 0:
        n /= 3
    return n == 1    #判断n是否为1，若n不是1，则n不是3的幂

#check n!= 0
#不考虑负数

时间复杂度：O(log3(n)) 不断地除以3

空间复杂度：O(1)

思路相同，但答案的代码简洁明了，望尘莫及T_T

Approach 2: Base Conversion(进制转换)

在10进制中，10，100，1000为10的幂

在2进制中，10，100，100为2的幂

在3进制中，

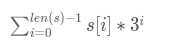
102 = 1*3^2+0*3^1+2*3^0

因此，在该式子中，当只有其中一个系数为1、 其它系数都为0时，这个3进制表示的数一定为3的幂。

所以需要：1.进制转换 2.判断1和0的情况（正则）

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        import re
        def dec_to_tri(num):
            l = []
            while True:
                num, reminder = divmod(num, 3)
                l.append(str(reminder))
                if num == 0:
                    return "".join(l[::-1])
        if n < 0:
            return False
        else:
            return(re.match("^10*$",dec_to_tri(n)))

时间复杂度：O(log3(n))

　　进制转换的原理是不断地除以3，所以复杂度为O(log3(n))

　　正则匹配的复杂度O(log3(n))

空间复杂度：O(log3(n))

　　比方法一多用了两个变量：

　　3进制表示的n（size O(log3(n))）

　　正则匹配的字符串 size constant

Approach 3: Mathematics（数学方法）

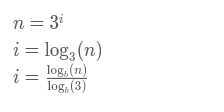
当且仅当i为整数时，n为3的幂

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        if n < 1:
            return False
        else:
            return math.log10(n)/math.log10(3)%1 == 0

#时间复杂度：未知，math.log操作限制了我们算法的时间复杂度，具体取决于我们使用的语言和编译器

#空间复杂度：O(1) 未使用其它变量

Approach 4: Integer Limitations

因为int范围内最大3的幂次方是3^19次方1162261467 只要判断能能否被这个数整除即可：

class Solution:
    def isPowerOfThree(self, n: int) -> bool:
        if n < 1:
            return False
        else:
            return 1162261467 % n == 0

#时间复杂度：O(1)  只有判断和除法

#空间复杂度：O(1) 

Performance Measurements

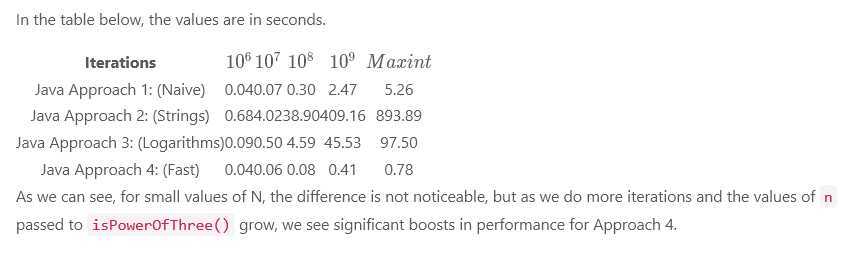
 在Java中的运行情况，数字代表运行的时间，单位：秒。

当N数值较小时，4种方法的表现差异不大。随着N数值增大，我们能发现方法四是性能最好的一种方法。

Conclusion

Simple optimizations like this might seem negligible, but historically, when computation power was an issue, it allowed certain computer programs (such as Quake 3 ^[4]) possible.

当处理的数据规模较小时，似乎没有必要研究如此多的方法。

当处理的数据规模增大时，有些方法的优势就显现出来了，特别计算力不够、数据又十分庞大的情况下。

 所以，我还是想不到后面两种方法。。。太优（BIAN）秀(TAI)了

Ref: https://leetcode.com/explore/featured/card/top-interview-questions-easy/102/math/745/

【LeetCode】【 Math】 判断一个数字是不是3的幂

原文：https://www.cnblogs.com/jialinliu/p/12733417.html