1.本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性
一.回归算法属于监督学习,线性回归就属于其中一个知识点。
二.线性回归就是多个自变量和因变量组合形成的线性关系。
三.统计学习中用到线性回归算法,它通过误差的评分合/最小二乘法。同时如果要将误差变最小,是再通过正规方程/梯度下降。
四.可以帮助我们预测一些数据,对此进行一定的判断,减少错误
本节学习代码:
import random import time import matplotlib.pyplot as plt # 梯度下降 xs = [0.1*x for x in range(0,10)] ys = [12*i+4 for i in xs] print(xs) print(ys) w = random.random() b = random.random() a1=[] b1=[] for i in range(10): #(1) for x,y in zip(xs,ys): o = w*x + b #预测值 e = (o-y) #误差 loss = e**2 dw = 2*e*x #求导 db = 2*e*1 w = w - 0.1*dw #0.1是学习率,这个要计 b = b - 0.1*db print(‘loss={0}, w={1}, b={2}‘.format(loss,w,b)) a1.append(i) b1.append(loss) plt.plot(a1,b1) plt.pause(0.1) plt.show()
2.思考线性回归算法可以用来做什么?(大家尽量不要写重复)
一、金融,分析企业债务期限结构与地区的市场化程度关系
二、教学预测,根据学生的学习基础来预测和分析当前课程成绩,改进教学方法
三、流行病学,有关吸烟对死亡率和发病率影响的早期证据
3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。(加分题)
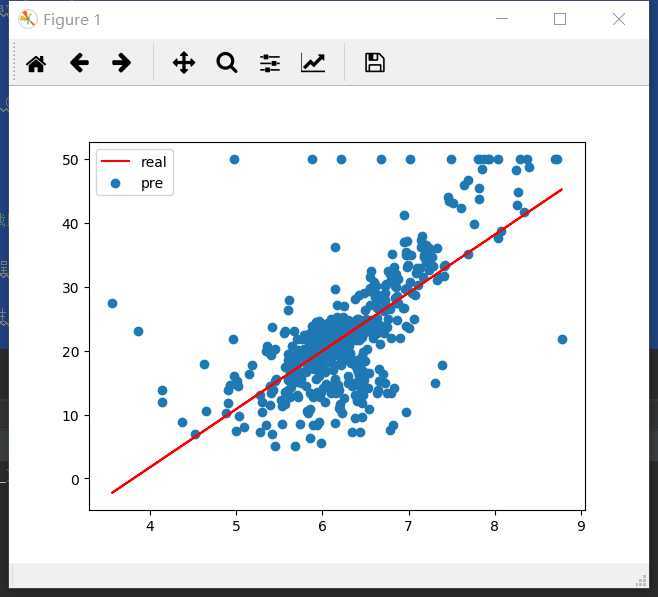
运用线性回归算法预测波士顿房价
代码:
from sklearn.datasets import load_boston from sklearn.linear_model import LinearRegression import matplotlib.pyplot as plt data=load_boston() data_all = data[‘data‘] x=data_all[:,5:6] #x[0] array([6.575]) numpy.ndarray type(x[0]) x[0] type(x[0]) y=data[‘target‘] #y[0] 24.0 numpy.float64 y[0] type(y[0]) model_LR=LinearRegression() model_LR.fit(x,y) print(‘模型的权值:‘,model_LR.coef_,‘截距项:‘,model_LR.intercept_) pre=model_LR.predict(x) #使用可视化的方式对比拟合出的线性回归方程与真是房价的分布情况 plt.scatter(x,y) #真实房价的分布 plt.plot(x,pre,c=‘r‘) #拟合出的线性回归方程 plt.legend([‘real‘,‘pre‘]) plt.show()
截图:
原文:https://www.cnblogs.com/q1uj1e/p/12738765.html