概率密度函数与最大似然估计的区别

概率密度函数（PDF）

以高斯分布的概率密度函数（PDF）为例，
\(f(x)=\frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x - \mu}{\sigma}\right)^2}\)

期望值\(\mu\)和方差\(\sigma\)确定之后，\(f(x)\)是\(x\)的PDF函数。更一般地， \(f(x)\)可以认为是\(x\)和\(\theta(\mu, \sigma)\)的函数，
\(f(x;\theta)=\frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x - \mu}{\sigma}\right)^2}\)

最大似然估计（maximum likelihood estimation）

现已知数据集 \(x=\{x_0, x_1, x_2, ...\}\) ，求使得 \(f(x)\) 最大化的参数 \(\theta\)，此时 \(f(x;\theta)\) 是模型参数 \(\theta\) 的函数，
\( f(\theta)=\frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x - \mu}{\sigma}\right)^2} \)
在所有 \(\theta\) 的可能取值中，最大似然估计求解使得 \(f(\theta)\) 最大化的参数值 \(\hat{\theta}\)

用大神Aurélien书里的一张图来总结一下：

概率密度函数与最大似然估计的区别

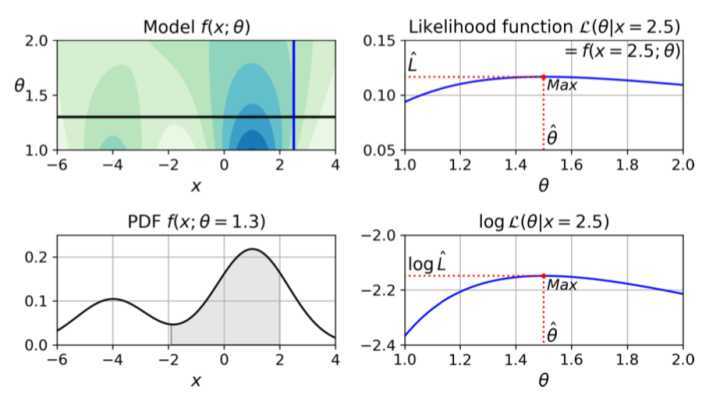
原文：https://www.cnblogs.com/yaos/p/12740004.html