栈

定义:

栈(Stack),是运算受限的线性表,插入和取出操作都只能在表头进行,也称之为后进先出(LIFO)线性表;

案例:

有名为stk的栈,按顺序插入:1,2,3三个元素,插入完成后取出全部,顺序为:3,2,1;

栈的实现:

既然是线性表,则可以通过顺序结构和链接结构来实现,通过顺序结构实现的栈称为顺序栈,通过链接结构实现的栈称为链栈;

常用操作:

• 初始化
• 入栈
• 出栈
• 空栈判断

顺序实现

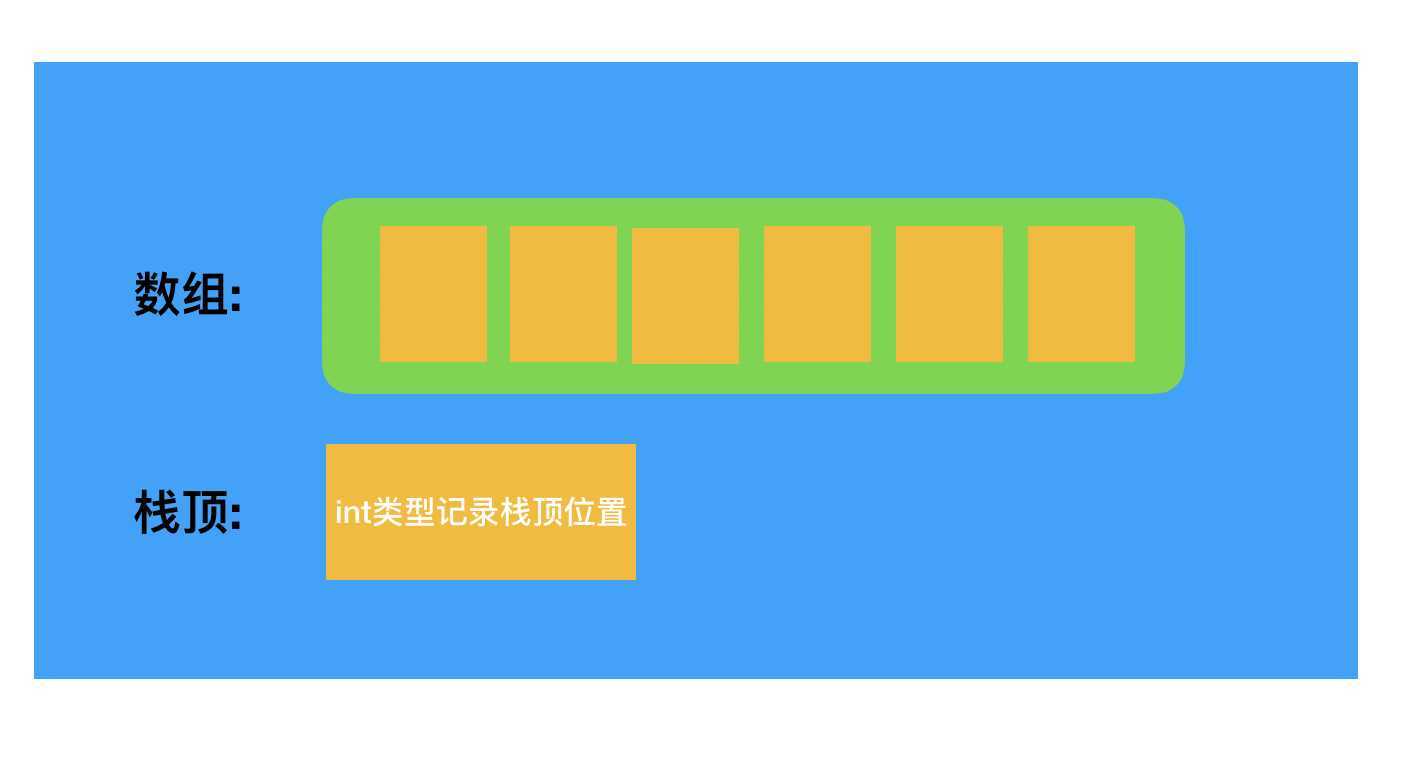
顺序栈数据结构:

c语言实现:

#include <stdio.h>

//栈的顺序实现
//定义数据结构
const int SIZE = 5;
typedef struct{
    int data[SIZE];
    int top;
}seqStk,*SEQStack;

SEQStack initalStack(){
    SEQStack stack = malloc(sizeof(seqStk));
    stack->top = -1;
    return stack;
}

int isEmpty(SEQStack stack){
    if(stack->top == -1){
        return 1;
    }
    return 0;
}

int getTop(SEQStack stack){
    if (isEmpty(stack)) {
        printf("err:stack is empty!\n");
        return NULL;
    }else{
        return stack->data[stack->top];
    }
}

int pop(SEQStack stack){
    //先进后出,出栈是判断是否空
     if (isEmpty(stack)) {
           printf("err:stack is empty!\n");
           return NULL;
     }else{
         int temp = getTop(stack);
         stack->top--;
         return temp;
     }
}


void push(SEQStack stack,int data){
    if (stack->top == SIZE-1) {
        printf("err:stack already full!\n");
    }else{
        stack->top++;
        stack->data[stack->top] = data;
    }
}


int main(int argc, const char * argv[]) {
    SEQStack stack = initalStack();
    push(stack,100);
    push(stack,200);
    push(stack,300);
    push(stack,400);
    push(stack,500);
    push(stack,600);
    printf("geted:%d\n",pop(stack));
    printf("geted:%d\n",getTop(stack));
    printf("geted:%d\n",pop(stack));
    printf("geted:%d\n",pop(stack));
    printf("geted:%d\n",pop(stack));
    printf("geted:%d\n",pop(stack));
    printf("Hello, World!\n");
    return 0;
}

双栈

顺序实现的弊端就在于,无法预估数据长度,会造成空间浪费,为了避免这个问题,我们可以让两个栈共享同一个顺序存储空间,起始地址和结束地址分别作为两个栈的栈底;

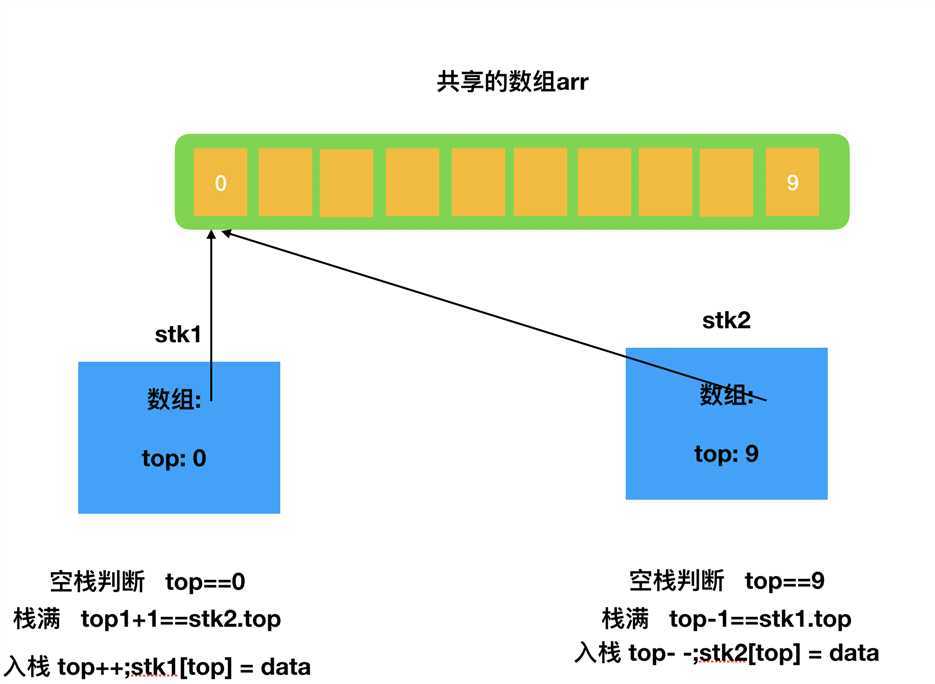
• 数据结构即相关操作:

链接实现

数据结构:

c语言实现:

#include <stdio.h>

//结构定义
typedef struct node{
    int data;
    struct node *next;
}Node,*LinkStk;

LinkStk initialStack(){
    LinkStk stack = malloc(sizeof(Node));
    stack->next = NULL;
    return stack;
}

int isEmpty(LinkStk stack){
    if (stack->next == NULL) {
        return 1;
    }
    return 0;
}

void push(LinkStk stack,int data){
    Node *p = malloc(sizeof(Node));
    p->next = stack->next;
    p->data = data;
    stack->next = p;
}

Node *getTop(LinkStk stack){
    return stack->next;
}

void *pop(LinkStk stack){
    if (isEmpty(stack)) {
        printf("error:stack is empty!\n");
        return NULL;
    }
    Node *temp = stack->next;
    stack->next = temp->next;
    free(temp);
}

int main(int argc, const char * argv[]) {
    LinkStk stack = initialStack();
    push(stack, 100);
    push(stack, 200);
    push(stack, 300);

    pop(stack);
    pop(stack);
    pop(stack);

    Node *a = getTop(stack);
    if (a != NULL){
        printf("%d\n",a->data);
    }

    push(stack, 900);
    Node *w = getTop(stack);
    printf("%d\n",w->data);
    printf("Hello, World!\n");
    return 0;
}

案例中所有操作算法时间复杂度均为O(1);

栈与队列

原文：https://www.cnblogs.com/yangyuanhu/p/12745053.html