冒泡排序:
外层循环N-1次,内循环每两个相邻的数相比较,如果前面的比后面大,二者交换。每一次外循环的结果是前N-i个数中最大的数放第N-i个位置(下标N-i-1)。将N-1个数处理完后,剩下的一个数自然在第一个位置,不需要处理,所以是N-1次外循环。
时间复杂度:
最坏:O(N^2)
最好:O(N)
1 void bubble_sort(long int a[]) 2 { 3 for (int i = 0; i < N-1; i++) 4 { 5 int flag=0; 6 for (int j = 0; j < N-i-1; j++) 7 { 8 if (a[j] > a[j + 1]) 9 { 10 flag =1; 11 long int temp = a[j]; 12 a[j] = a[j + 1]; 13 a[j + 1] = temp; 14 } 15 } 16 if(flag == 0) break; 17 } 18 }
插入排序:
把当前数前面比当前数大的往后移动一位,再把当前数填到移出的空位中。
时间复杂度:
最坏:O(N^2)
最好:O(N)
1 void Insert_sort(elemtype a[], int n ) 2 { 3 for (int i = 1; i < n; i++) 4 { 5 int j; 6 elemtype tmp = a[i]; 7 for (j = i; j > 0 && tmp < a[j - 1]; j--) 8 { 9 a[j] = a[j - 1]; 10 } 11 a[j] = tmp; 12 } 13 }
选择排序:
每次循环在无序序列中选一个最小的放到有序序列(的最后一个位置)中。
时间复杂度:
θ(n^2)
1 void selection_sort(elemtype a[], int n) 2 { 3 for(int i=0;i<n-1;i++) 4 { 5 int min = i; 6 for(int j=i;j<n;j++) 7 { 8 if(a[j] < a[min]) 9 min = j; 10 } 11 if(min != i) 12 { 13 int tmp = a[i]; 14 a[i] = a[min]; 15 a[min] = tmp; 16 } 17 } 18 }
希尔排序:
间隔为increment的元素相互比较排序,increment的值每次循环减半(或其他)。
时间复杂度:
最坏:θ(n^2)
可选其他增量,进一步优化。
1 void Shell_sort(elemtype a[]) 2 { 3 int k; 4 int Increment; 5 for (Increment = N / 2; Increment >= 1; Increment /= 2) 6 { 7 for (int j = Increment; j < N; j++) 8 { 9 int tmp = a[j]; 10 for (k = j; k - Increment >= 0; k -= Increment) 11 { 12 if (tmp < a[k - Increment]) 13 { 14 a[k] = a[k - Increment]; 15 } 16 else break; 17 } 18 a[k] = tmp; 19 } 20 } 21 }
归并排序:
分而治之,使用递归将小序列排序再合并成大序列,再排序,再合并成更大序列,直至完成所有元素的排序。
时间复杂度:
O(NlogN)
额外空间复杂度:
O(N)
1 void merge(elemtype a[], elemtype tmp[], int L, int R, int RE) 2 { 3 int LE = R - 1; 4 int num = RE - L + 1; 5 int L2 = L; 6 while (L <= LE && R <= RE) 7 { 8 if (a[L] <= a[R]) 9 { 10 tmp[L2++] = a[L++]; 11 } 12 else if (a[R] < a[L]) 13 { 14 tmp[L2++] = a[R++]; 15 } 16 } 17 while (L <= LE) 18 { 19 tmp[L2++] = a[L++]; 20 } 21 while (R <= RE) 22 { 23 tmp[L2++] = a[R++]; 24 } 25 for (int i = 0; i < num; i++, RE--) 26 { 27 a[RE] = tmp[RE]; 28 } 29 } 30 31 void Msort(elemtype a[], elemtype tmp[], int L, int R) 32 { 33 int C; 34 if (L < R) 35 { 36 C = (L + R) / 2; 37 Msort(a, tmp, L, C); 38 Msort(a, tmp, C + 1, R); 39 merge(a, tmp, L, C + 1, R); 40 } 41 } 42 43 void Merge_sort(elemtype a[]) 44 { 45 elemtype* tmp = new elemtype[N * sizeof(elemtype)]; 46 if (NULL == tmp) 47 { 48 cerr << "error" << endl; 49 return; 50 } 51 else 52 { 53 Msort(a, tmp, 0, N - 1); 54 delete[]tmp; 55 } 56 }
快速排序:median3()选中枢元,以中枢元为界,比中枢元小的放左边,比中枢元大的放右边,再分别递归处理左右。
时间复杂度:
平均:O(NlogN)
最坏:O(N^2),当中枢元是边界值
额外空间复杂度:
O(logN)(递归)
1 elemtype median3(elemtype a[], int L, int R) 2 { 3 int C = (L + R) / 2; 4 if (a[L] > a[C]) swap(&a[L], &a[C]); 5 if (a[L] > a[R]) swap(&a[L], &a[R]); 6 if (a[C] > a[R]) swap(&a[C], &a[R]); 7 //swap(&a[R], &a[R - 1]); 8 swap(&a[R-1], &a[C]); 9 return a[R-1]; 10 } 11 12 void Qsort(elemtype a[], int L, int R) 13 { 14 int pivot,i,j; 15 if (L + 3 <= R) 16 { 17 i = L; 18 j = R - 1; 19 pivot = median3(a, L, R); 20 while (1) 21 { 22 while (a[++i] < pivot) {} 23 while (a[--j] > pivot) {} 24 if (i < j) 25 { 26 swap(&a[i], &a[j]); 27 } 28 else 29 break; 30 } 31 swap(&a[i], &a[R - 1]); 32 Qsort(a, L, i-1); 33 Qsort(a, i + 1, R); 34 } 35 else 36 Insert_sort(a + L, R - L + 1); 37 } 38 39 void Quick_sort(elemtype a[]) 40 { 41 Qsort(a, 0, N - 1); 42 }
堆排序:perdown()将树调整为大顶堆,每次a[0]与a[i]交换,再调整0-i的树为大顶堆。
时间复杂度:
O(NlogN)
1 void percdown(elemtype a[], int r, int N)//此函数作用:在根节点,左子和右子之间,选出最大的一个作为新的根节点,循环的作用:使得交换数据后的子节点为根的树同样满足根节点最大的条件(可以用递归实现)。 2 { 3 int child; 4 int temp; 5 //for (i = N / 2; 2*i + 1 < N; i = child) 6 temp = a[r]; // temp 不需要动 7 for (; 2 * r + 1 < N; r = child) 8 { 9 child = 2 * r + 1; 10 if (2 * r + 2 < N && a[2 * r + 2] > a[2 * r + 1]) //如果下标不越界而且右子大于左子 11 child++;//child更新为右子的下标 12 if (a[child] > temp&& child < N) //如果子确实大于个根,则交换二者的值,否则不进行任何操作,直接退出。这一步实际上完成了:根,左,右三者比较且选出最大的一个值作为根节点。 13 { 14 a[r] = a[child]; 15 } 16 else 17 break; 18 } 19 a[r] = temp; //即a[child] = temp实现了a[r] 与 a[child]进行数据交换。 20 } 21 22 void Heap_Sort(elemtype a[]) 23 { 24 //build heap 25 for (int i = N / 2; i >= 0; i--)//从每一个根节点开始调用percdown(0 - N/2) 26 { 27 percdown(a, i, N); 28 } 29 //delete max 30 for (int i = N - 1; i > 0; i--) //交换数组的第一个数据和最后一个数据,然后进行一次percdown调整为大顶堆,再进行下一次循环。 31 { 32 swap(&a[0], &a[i]); 33 percdown(a, 0, i); 34 } 35 }

1 #include <iostream> 2 #include <string> 3 #include <cmath> 4 #include <math.h> 5 6 using namespace std; 7 typedef long int elemtype; 8 int N; 9 10 void bubble_sort(long int a[]) 11 { 12 for (int i = 0; i < N-1; i++) 13 { 14 int flag=0; 15 for (int j = 0; j < N-i-1; j++) 16 { 17 if (a[j] > a[j + 1]) 18 { 19 flag =1; 20 long int temp = a[j]; 21 a[j] = a[j + 1]; 22 a[j + 1] = temp; 23 } 24 } 25 if(flag == 0) break; 26 } 27 } 28 29 30 void Insert_sort(elemtype a[], int n ) 31 { 32 for (int i = 1; i < n; i++) 33 { 34 int j; 35 elemtype tmp = a[i]; 36 for (j = i; j > 0 && tmp < a[j - 1]; j--) 37 { 38 a[j] = a[j - 1]; 39 } 40 a[j] = tmp; 41 } 42 } 43 44 void selection_sort(elemtype a[], int n) 45 { 46 for(int i=0;i<n-1;i++) 47 { 48 int min = i; 49 for(int j=i;j<n;j++) 50 { 51 if(a[j] < a[min]) 52 min = j; 53 } 54 if(min != i) 55 { 56 int tmp = a[i]; 57 a[i] = a[min]; 58 a[min] = tmp; 59 } 60 } 61 } 62 63 void Shell_sort(elemtype a[]) 64 { 65 int k; 66 int Increment=N/2; 67 for (Increment = N / 2; Increment >= 1; Increment /= 2) 68 { 69 for (int j = Increment; j < N; j++) 70 { 71 int tmp = a[j]; 72 for (k = j; k - Increment >= 0; k -= Increment) 73 { 74 if (tmp < a[k - Increment]) 75 { 76 a[k] = a[k - Increment]; 77 } 78 else break; 79 } 80 a[k] = tmp; 81 } 82 } 83 } 84 85 void swap(elemtype* a, elemtype* b) 86 { 87 int temp = *a; 88 *a = *b; 89 *b = temp; 90 } 91 92 void percdown(elemtype a[], int r, int N)//此函数作用:在根节点,左子和右子之间,选出最大的一个作为新的根节点,循环的作用:使得交换数据后的子节点为根的树同样满足根节点最大的条件(可以用递归实现)。 93 { 94 int child; 95 int temp; 96 //for (i = N / 2; 2*i + 1 < N; i = child) 97 temp = a[r]; // temp 不需要动 98 for (; 2 * r + 1 < N; r = child) 99 { 100 child = 2 * r + 1; 101 if (2 * r + 2 < N && a[2 * r + 2] > a[2 * r + 1]) //如果下标不越界而且右子大于左子 102 child++;//child更新为右子的下标 103 if (a[child] > temp&& child < N) //如果子确实大于个根,则交换二者的值,否则不进行任何操作,直接退出。这一步实际上完成了:根,左,右三者比较且选出最大的一个值作为根节点。 104 { 105 a[r] = a[child]; 106 } 107 else 108 break; 109 } 110 a[r] = temp; //即a[child] = temp实现了a[r] 与 a[child]进行数据交换。 111 } 112 113 void Heap_Sort(elemtype a[]) 114 { 115 //build heap 116 for (int i = N / 2; i >= 0; i--)//从每一个根节点开始调用percdown(0 - N/2) 117 { 118 percdown(a, i, N); 119 } 120 //delete max 121 for (int i = N - 1; i > 0; i--) //交换数组的第一个数据和最后一个数据,然后进行一次percdown调整为大顶堆,再进行下一次循环。 122 { 123 swap(&a[0], &a[i]); 124 percdown(a, 0, i); 125 } 126 } 127 128 void merge(elemtype a[], elemtype tmp[], int L, int R, int RE) 129 { 130 int LE = R - 1; 131 int num = RE - L + 1; 132 int L2 = L; 133 while (L <= LE && R <= RE) 134 { 135 if (a[L] <= a[R]) 136 { 137 tmp[L2++] = a[L++]; 138 } 139 else if (a[R] < a[L]) 140 { 141 tmp[L2++] = a[R++]; 142 } 143 } 144 while (L <= LE) 145 { 146 tmp[L2++] = a[L++]; 147 } 148 while (R <= RE) 149 { 150 tmp[L2++] = a[R++]; 151 } 152 for (int i = 0; i < num; i++, RE--) 153 { 154 a[RE] = tmp[RE]; 155 } 156 } 157 158 void Msort(elemtype a[], elemtype tmp[], int L, int R) 159 { 160 int C; 161 if (L < R) 162 { 163 C = (L + R) / 2; 164 Msort(a, tmp, L, C); 165 Msort(a, tmp, C + 1, R); 166 merge(a, tmp, L, C + 1, R); 167 } 168 } 169 170 void Merge_sort(elemtype a[]) 171 { 172 elemtype* tmp = new elemtype[N * sizeof(elemtype)]; 173 if (NULL == tmp) 174 { 175 cerr << "error" << endl; 176 return; 177 } 178 else 179 { 180 Msort(a, tmp, 0, N - 1); 181 delete[]tmp; 182 } 183 } 184 185 elemtype median3(elemtype a[], int L, int R) 186 { 187 int C = (L + R) / 2; 188 if (a[L] > a[C]) swap(&a[L], &a[C]); 189 if (a[L] > a[R]) swap(&a[L], &a[R]); 190 if (a[C] > a[R]) swap(&a[C], &a[R]); 191 //swap(&a[R], &a[R - 1]); 192 swap(&a[R-1], &a[C]); 193 return a[R-1]; 194 } 195 196 void Qsort(elemtype a[], int L, int R) 197 { 198 int pivot,i,j; 199 if (L + 3 <= R) 200 { 201 i = L; 202 j = R - 1; 203 pivot = median3(a, L, R); 204 while (1) 205 { 206 while (a[++i] < pivot) {} 207 while (a[--j] > pivot) {} 208 if (i < j) 209 { 210 swap(&a[i], &a[j]); 211 } 212 else 213 break; 214 } 215 swap(&a[i], &a[R - 1]); 216 Qsort(a, L, i-1); 217 Qsort(a, i + 1, R); 218 } 219 else 220 Insert_sort(a + L, R - L + 1); 221 } 222 223 void Quick_sort(elemtype a[]) 224 { 225 Qsort(a, 0, N - 1); 226 } 227 228 int main() 229 { 230 cin >> N; 231 long int* a = new long int[N]; 232 for (int i = 0; i < N; i++) 233 { 234 int temp; 235 cin >> temp; 236 a[i] = temp; 237 } 238 //bubble_sort(a); 239 //selection_sort(a, N); 240 //Insert_sort(a, N); 241 //Shell_sort(a); 242 Heap_Sort(a); 243 //Merge_sort(a); 244 //Quick_sort(a); 245 246 for (int i = 0; i < N; i++) 247 { 248 if (i == N - 1) 249 cout << a[i]; 250 else 251 cout << a[i] << " "; 252 } 253 254 return 0; 255 }
结果对比:
冒泡:
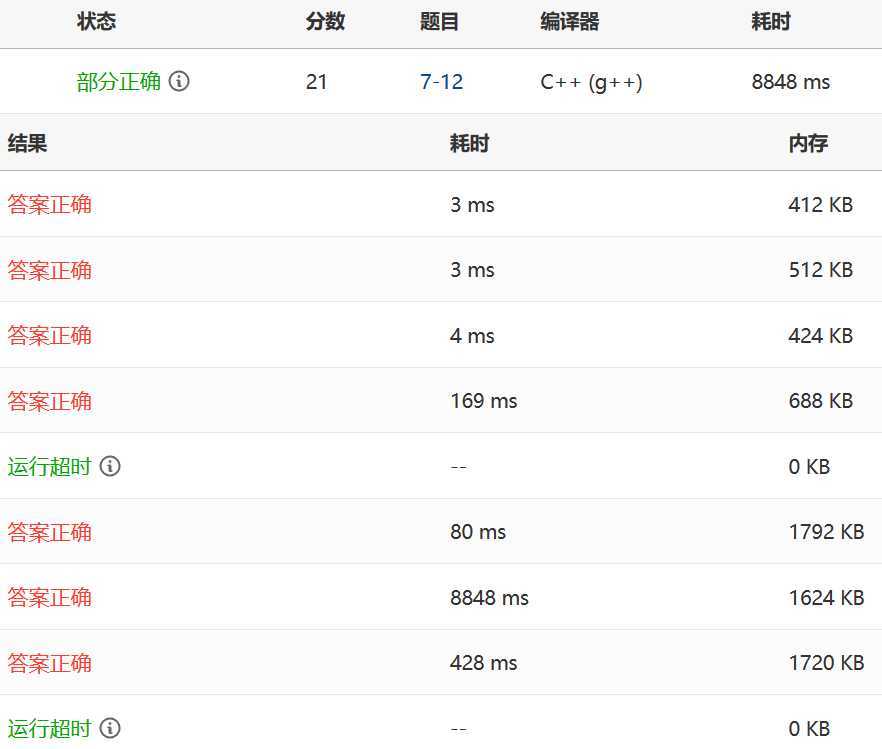
选择:
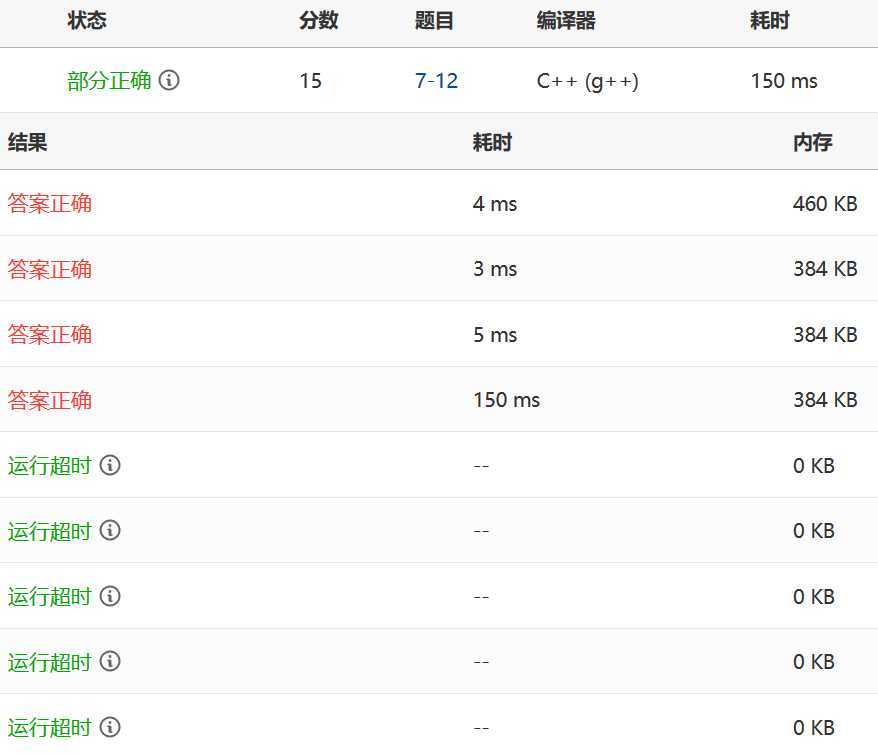
插入:
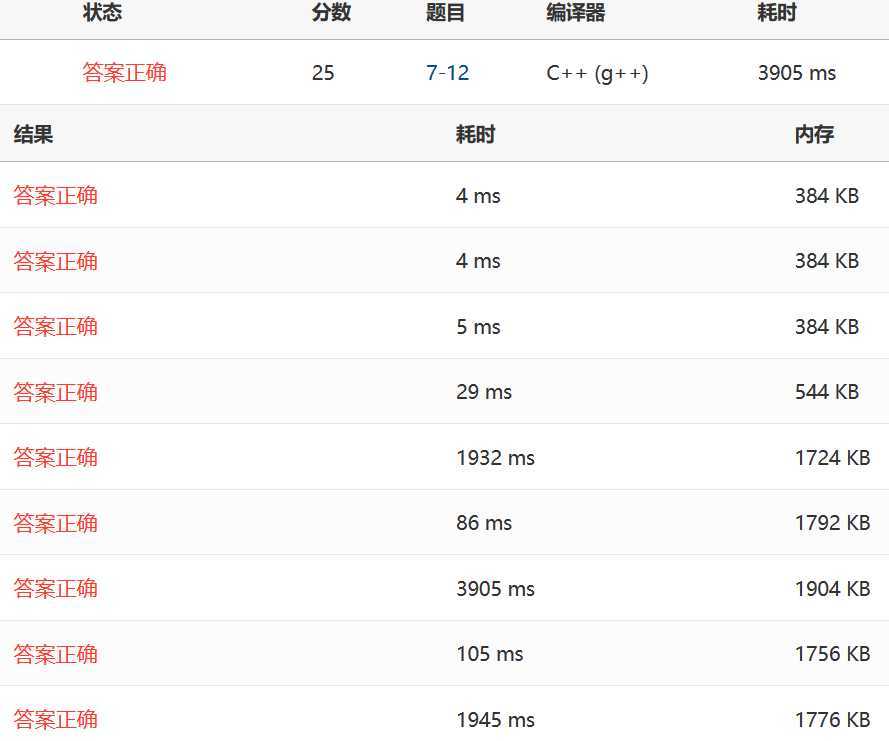
希尔:
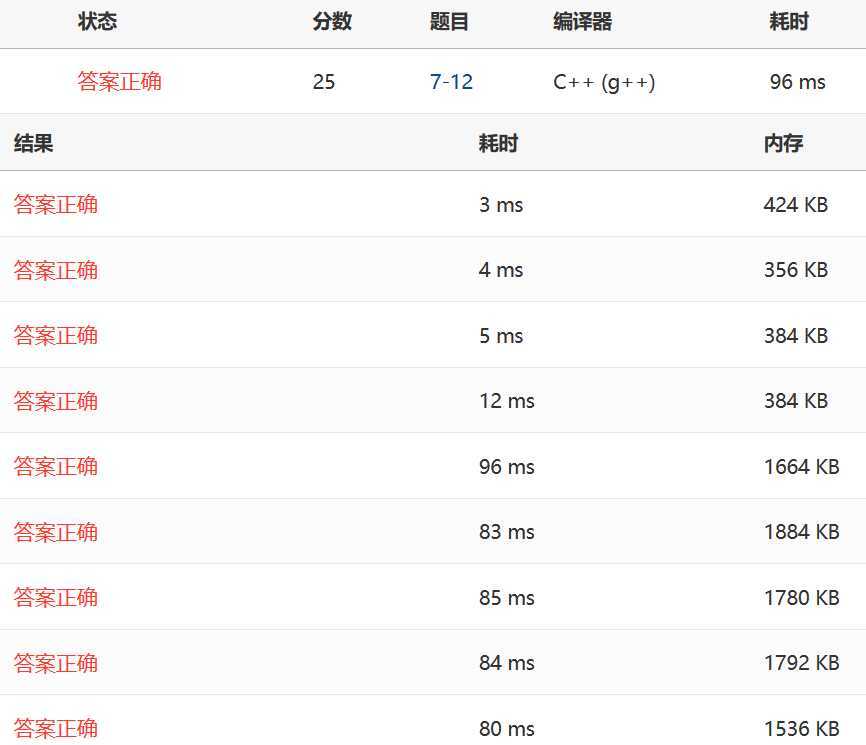
堆排:
归并:
快排:
原文:https://www.cnblogs.com/2020R/p/12730689.html