一、实验内容

      1.实验目的

三元组是数据结构里的一个重要概念，主要是用来存储稀疏矩阵的一种压缩方式，也叫三元组表。采用顺序存储结构来表示的三元组称为三元组顺序表。本实验使用高级编程C语言来构建一个三元组顺序表存储的稀疏n阶方阵，求解该方阵中两条对角线上的元素之和并实现该方阵的快速转置。体会并掌握数据结构中通过三元组存储结构实现矩阵压缩的方法和实践过程。

      2.实验内容

       1)  构建一个三元组顺序存储结构的抽象数据类型，通常应包含如下步骤：

            a.定义用来描述三元组的结构体变量类型Triple，成员包括i,j,value分别对应矩阵元素的行标、列标和值；

            b.编写一个矩阵压缩算法，记为zipMatrix操作（函数），将稀疏矩阵转化成三元组顺序表；

　　　c.编写一个矩阵对角线求和算法，记为sumMatrix操作（函数）；

            d. 编写一个快速转置算法，记为SwapMatrix操作（函数）；

      2）基于上述三元组顺序表存储的基本操作实现矩阵压缩和快速转置：

            a.在main函数内部声明一个包含少量非零值的二维数组和一个三元组结构体数组，分别表示稀疏矩阵和三元组顺序表；

            b.调用zipMatrix函数，将稀疏矩阵转化成三元组顺序表，实现矩阵压缩；

            c.调用swapMatrix函数，实现矩阵的快速转置;

            d.编译运行程序，评估实验结果.

      3）完成实验报告的填写

         3.实验原理

     （1）稀疏矩阵：在矩阵中，若数值为0的元素数目远远多于非0元素的数目，并且非0元素分布没有规律时，则称该矩阵为稀疏矩阵.

     （2）三元组顺序表存储的逻辑结构原理（即矩阵压缩原理）如下：

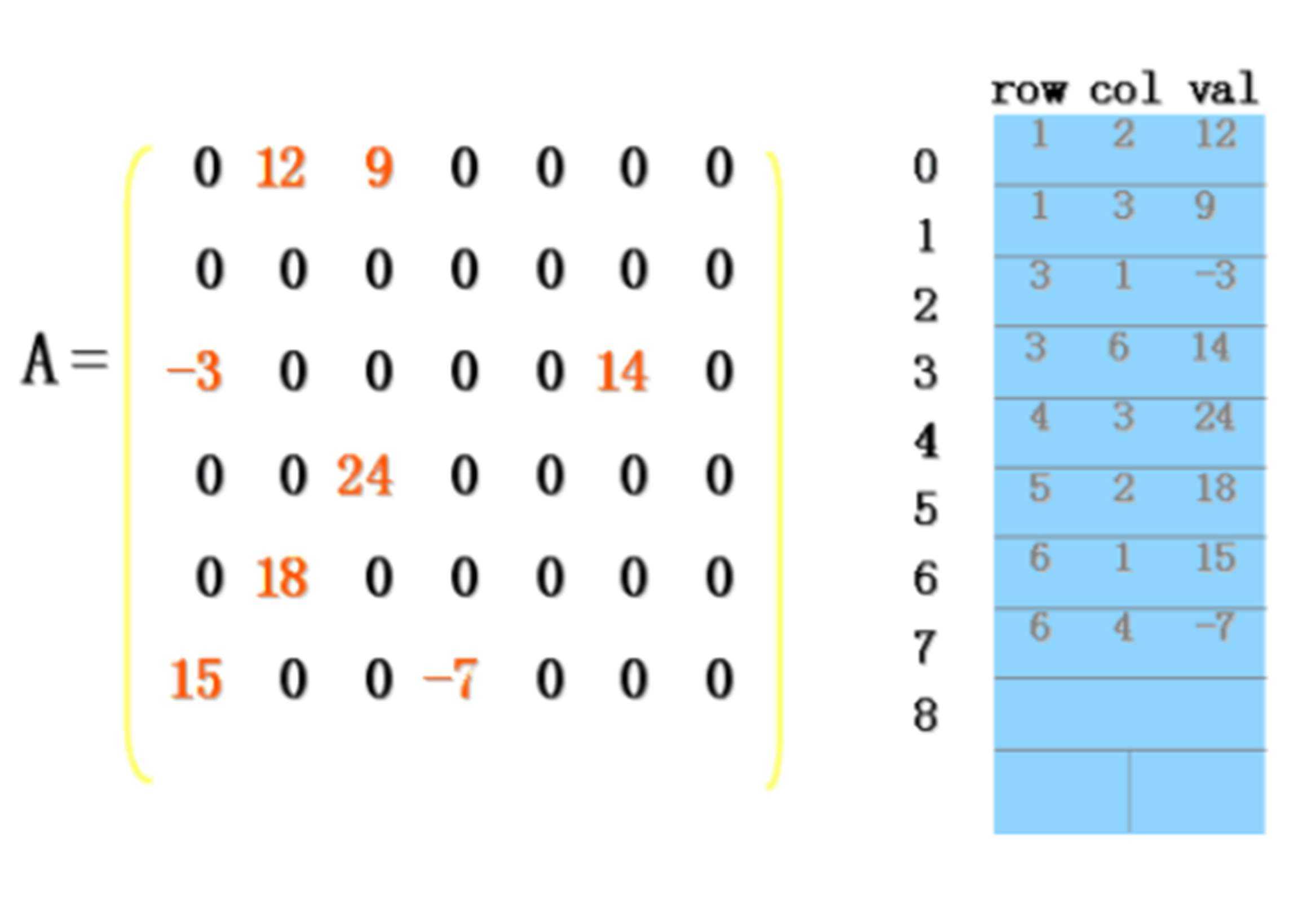
矩阵的转置实际上就是将数据元素的行标和列标互换，即 T(i,j) = M(j,i) 。

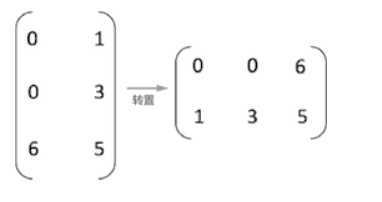
三元组相应地转变为：

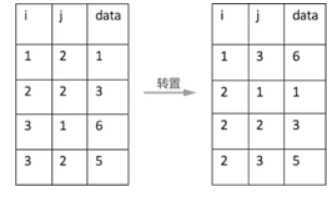
二、实验过程

1.Triple结构体定义

       首先用C/C++开发环境新建源文件，首先键入如下预定义命令行：

#include <stdio.h>
#define MAXSIZE 30
#define n 6

    使用C语言里的宏定义声明两个常量MAXSIZE和n，MAXSIZE表示三元组顺序表的初始化大小，n表示矩阵的阶数。

      接着，根据三元组顺序表的逻辑结构原理图，定义用来描述三元组数据对象的结构体变量类型Triple，代码如下：

typedef int ElemType;
/*
 定义三元组
*/ 
typedef struct{
    int i, j;
    ElemType value;
}Triple;

　　这里用i、j和value分别表示数据元素在稀疏矩阵的行标、列标和值（int型）。

2. zipMatrix函数

       编写矩阵压缩算法,在参数列表中接受一个n阶int型矩阵arr和一个三元组指针t。声明一个int变量index来统计矩阵压缩后获得的三元组顺序表的数据元素个数。row和col是用来遍历矩阵行和列的循环变量。遍历过程中，遇到非零元素，将其在稀疏矩阵中的行标（第一行记为1）、列标（第一列记为1）和元素值分别赋给当前指针t所指向的三元组顺序表元素的i、j和value。然后指针t自增指向下一个三元组顺序表元素。最终返回三元组顺序表的有效长度。

      代码如下：

/*
 矩阵压缩
*/
int zipMatrix(int arr[n][n], Triple *t){
    int index=0;
    int row,col;
    for(row=0;row<n;row++)
        for(col=0;col<n;col++){
            if(arr[row][col]!=0){
                t->i=row+1,t->j=col+1;
                t->value=arr[row][col];
                t++;
                index++;
            }
        }
    return index;
}

3. sumMatrix函数

       编写sumMatrix函数计算稀疏矩阵对角线上数据元素之和，对角线元素对应满足成员i等于成员j（主对角线元素）或者成员i与j之和为n+1的三元组顺序表元素。将符合条件的三元组的value值累加求和。

/*
 对角线求和
*/
int sumMatrix(Triple t[], int size){
    int sum=0;
    for(int k=0;k<size;k++){
        if(t[k].i==t[k].j||(t[k].i+t[k].j)==n+1){
            sum=sum+(t[k].value);
        }
    }
    return sum;
}

4. swapMatrix函数

       算法思路

       j表示数据元素的列标，由于经转置后以行标为主序（即原来的列标），所以首先统计出每一列的非零元素个数，上述为第一列1个元素、第二列2个元素、第三列2个元素、第四列0个元素、第五列0个元素、第六列1个元素和第七列1个元素。

用一个数组col来记录每一列的个数(数组索引对应列数)

接着计算每一列首个非零元的位置次序：

     用一个数组p来记录，默认第一列的首个非零元位置次序为1，p[1]=1,列标与索引一致；

      第二列首个非零元位置次序为1+col[1];

      以此类推，p[i]=p[i-1]+col[i-1],i=2,3,…,n;

最后遍历每个三元组表元素，由于i值递增，所以不同j值首次出现则对应该列的首个非零元。如果再次出现相同的j值，该三元组向后依次插入数组。

      上述三元组表经转置得到

      其中（1，2，4）（2，1，4）（3，1，7）（6，5，2）（7，3，8）分别是现各行首个非零元，次序为1，2，4，6和7.与上述表一致。算法设计可行且正确。

具体操作

       编写swapMatrix函数实现矩阵的快速转置（对应于三元组的转置），代码如下：

      1. 参数列表接收一个三元组顺序表（表现为Triple数组t）和一个int型变量size；

      2. 初始化一个大小为size的三元组顺序表T；

      3. 初始化三个大小为n+1的int数组p、col和num;

      4. 统计稀疏矩阵每一列的数据元素个数，并将第e列（e=1,2,…,n）的元素个数赋给col[e]；

      5. 计算每一列首个非零元的存储位序，默认第一列首个非零元的存储位序为1；

      6. 遍历三元组表t,实现快速转置得到转置后的三元组表T；

      7. 打印三元组表T;

/*
 快速转置
*/
void swapMatrix(Triple t[], int size){
    Triple T[size]={};
    int num[n+1]={};
    int p[n+1]={};
    int col[n+1]={};
    int temp,k;
     
    for(k=0;k<size;k++){
        col[t[k].j]++;
    }
    // 构造数组num,从num[1]开始表示每一列的非零元素的个数
    for(k=1;k<=n;k++){
        num[k]=col[k];
    }
    
    p[1]=1;
    // 构造数组p,从p[1]开始定位每一列的第一个非零元素的位置
    for(k=2;k<=n;k++){
        p[k]=p[k-1]+num[k-1];
    }
    // 快速转置
    for(k=0;k<size;k++){
          temp=p[t[k].j]-1;
        while(T[temp++].value!=0);
        T[temp-1].i=t[k].j;
           T[temp-1].j=t[k].i;
        T[temp-1].value=t[k].value;
    
    }
    // 遍历输出三元组顺序表T
    for(k=0;k<size;k++){
        printf("(%d,",T[k].i);
        printf("%d,",T[k].j);
        printf("%d)",T[k].value);
    }
}

5. main函数的实现

int main(){
    // 定义一个矩阵（二维数组）
    int arr[n][n]={{0,0,6,4,0,9},
        {7,3,8,0,0,0},{0,4,0,2,0,0},
        {6,3,0,0,0,1},{4,0,9,0,1,0},
        {3,0,0,0,7,0}
    };
    // 初始化一个三元组
    Triple t[MAXSIZE]={};
    // 定义一个三元组指针
    Triple *T=t;
    // 调用zipMatrix函数，返回int
    int size=zipMatrix(arr,T);
    // 调用sumMatrix函数，返回int
    int sum=sumMatrix(t,size);
    
    printf("对角线元素之和为%d\n",sum);
    printf("原三元组\n");
    // 打印原三元组顺序表
    for(int k=0;k<size;k++){
        printf("(%d,",t[k].i);
        printf("%d,",t[k].j);
        printf("%d)",t[k].value);
    }
    printf("\n");
    printf("经转置的三元组\n");
    // 调用swapMatrix函数，实现快速转置
    swapMatrix(t,size);
    return 0;
}

1. 声明一个n阶的int型稀疏方阵arr，并初始化；

      2. 初始化一个大小为MAXSIZE的三元组数组t和一个初始值指向数组t基地址的指针T；

      3. 调用zipMatrix函数并传入参数arr和T，返回值赋给size；

      4. 调用sumMatrix函数并传入参数t和size，返回值赋给sum；

      5. 打印原三元组顺序表；

      6. 调用swapMatrix函数并传入参数t和size，实现快速转置；

      7. 编译运行，测试代码.

三、实验结果

实验结果与预期目标一致，能够实现三元组顺序表存储稀疏矩阵、能够正确计算出n阶方阵对角线元素之和以及实现方阵的快速转置（用三元组表来表示）。

四、实验总结

       通过“三元组顺序表存储的稀疏矩阵练习”这个实验，利用三元组顺序结构来实现对稀疏矩阵的压缩存储、计算对角线元素之和以及对n阶方阵的快速转置。

在实验的过程中，体会到了采用三元组顺序表存储稀疏矩阵的优点，就本实验而言，稀疏矩阵中的非零元远少于零元，从存储空间的意义来看，稀疏矩阵浪费了一定的存储资源。而通过矩阵压缩，使用三元组表来存储稀疏矩阵会大大减少不必要的空间开销。

       三元组顺序表结构对于实现n阶方阵的快速转置有着重要的作用。普通转置需要从行和列两个维度遍历数据元素，时间复杂度为O(n^2)。而快速转置利用每一列中首个非零元的具体位置来实现一次遍历即可转置。本实验采用三元组转置来表示方阵的转置。

总的来说加深理解有关三元组顺序表结构实现稀疏矩阵压缩存储和快速转置，并体会和了解选择不同的数据结构会影响算法的空间复杂度和时间复杂度。

三元组顺序表存储的稀疏矩阵练习

原文：https://www.cnblogs.com/angoli/p/12748958.html