线性DP-最短编辑距离、编辑距离

902. 最短编辑距离

给定两个字符串A和B，现在要将A经过若干操作变为B，可进行的操作有：

1. 删除–将字符串A中的某个字符删除。
2. 插入–在字符串A的某个位置插入某个字符。
3. 替换–将字符串A中的某个字符替换为另一个字符。

现在请你求出，将A变为B至少需要进行多少次操作。

输入格式

第一行包含整数n，表示字符串A的长度。

第二行包含一个长度为n的字符串A。

第三行包含整数m，表示字符串B的长度。

第四行包含一个长度为m的字符串B。

字符串中均只包含大写字母。

输出格式

输出一个整数，表示最少操作次数。

数据范围

1≤n,m≤1000

输入样例：

10 
AGTCTGACGC
11 
AGTAAGTAGGC

输出样例：

4

动态规划之所以比暴搜快：是因为DP可以用一个东西来表示一堆东西。不用朴素的枚举每一种方案。所以它比较快，这是一种
比较感性的理解DP。
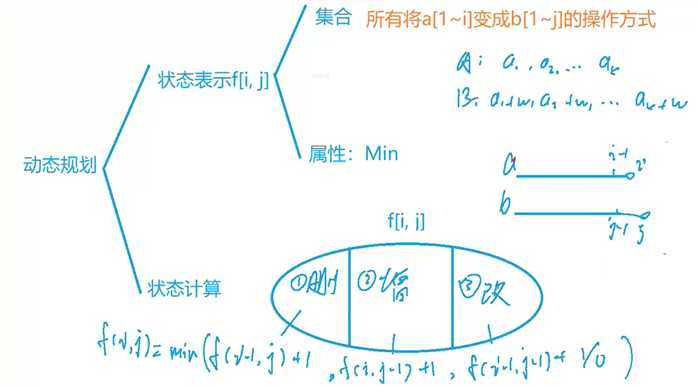
状态表示f[i][j]集合: 所有将a[1~i]变成b[1~j]的操作方式。
属性：所有操作方式的最小值。
删：
f[i,j] = f[i-1, j) + 1, 删除a[i]之前a[i-1] = b[j]
增：
f[i, j] = f[i,j-1] + 1,增加之前a[i]=b[j-1],在a[i]后加的其实是b[j].
改：
f[i, j] = f[i-1, j-1],更改a[i] = b[j]。但改之前a[i-1] = b[j-1].
取上面三个并的最小值。
可以看出：考虑在操作之前的条件是什么？然后增加这个条件之后达到的状况并且数量+1.

#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1001;
int n, m;
char a[N], b[N];
int f[N][N];

int main()
{
    cin>>n>>a+1>>m>>b+1;
    
    for(int i = 0; i <= m; i++) f[0][i] = i;//添加操作的初始化，b有几个字母就有几个操作。
    for(int i = 0; i <= n; i++) f[i][0] = i;//删除操作，a多了几个字母就删几个，操作主体都是a
    
    
    
    for(int i = 1;i<=n;i++)
        for(int j = 1;j <= m;j++)
        {
            f[i][j] = min(f[i-1][j] + 1, f[i][j-1] + 1);
            if(a[i] == b[j]) f[i][j] = min(f[i][j], f[i-1][j-1]);
            else f[i][j] = min(f[i][j], f[i-1][j-1] + 1);//不相同，则实行更改操作使得a[i] = b[j]
        }
        
    cout<<f[n][m]<<endl;    
    
}

线性DP-最短编辑距离、编辑距离

原文：https://www.cnblogs.com/longxue1991/p/12749160.html