树的相关概念
树这种数据结构模拟了自然界中树的概念,自然界中的树有根、叶子、枝干,数据结构中的树也是如此,只不过是倒过来的:
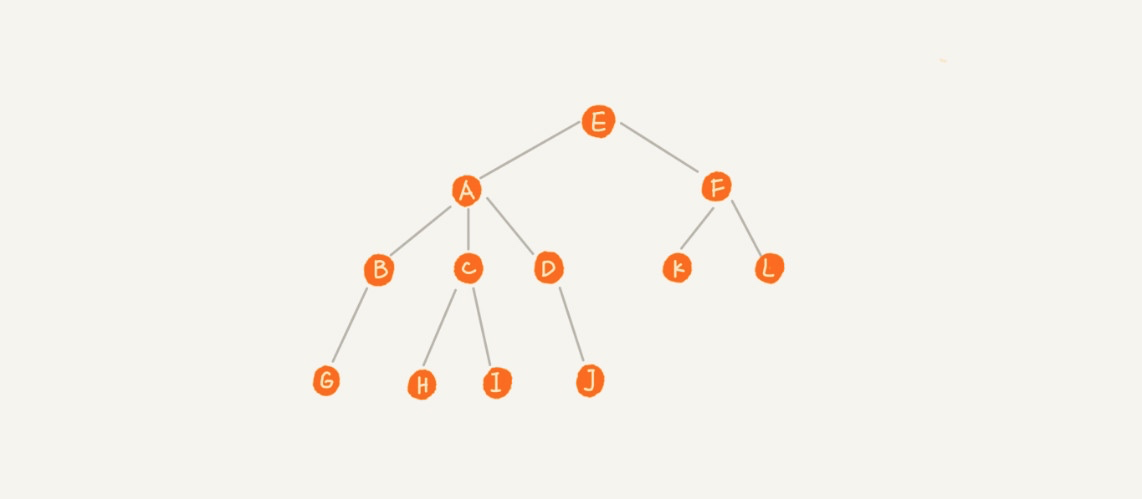
其中的每个元素叫做节点。树的顶点(没有父元素的节点)叫根节点,如 E;每个分支的末端节点(没有子元素的节点)叫叶子节点,如 G、H、I、J、K、L;用来连接相邻节点之间的关系叫父子关系,比如 E 是 A、F 的父节点,A、F 是 E 的子节点;具有同一个父节点的多个子节点叫做兄弟节点,比如 A、F 是兄弟节点。
节点拥有的子节点数目叫做节点的度,显然,叶子节点的度为 0,树的度是树内各节点度的最大值。
除此之外,树还有高度、深度和层的概念:

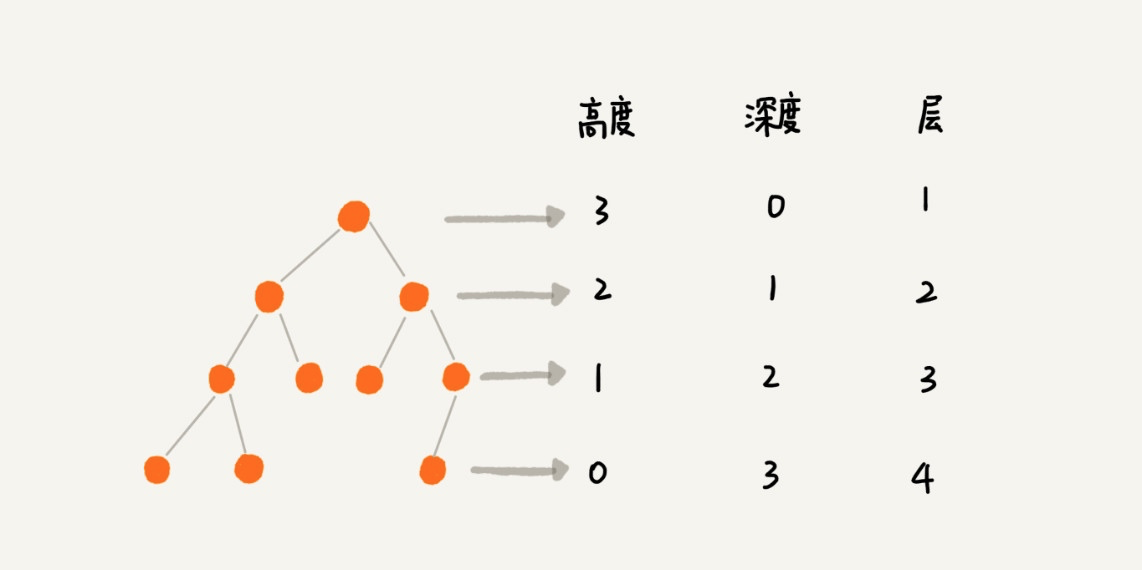
注:其实线性表也可以看作一种特殊的树,只不过所有节点都在一个分支上,第一个元素是根节点,最后一个元素是子节点,没有兄弟节点。层数就是线性表的长度。
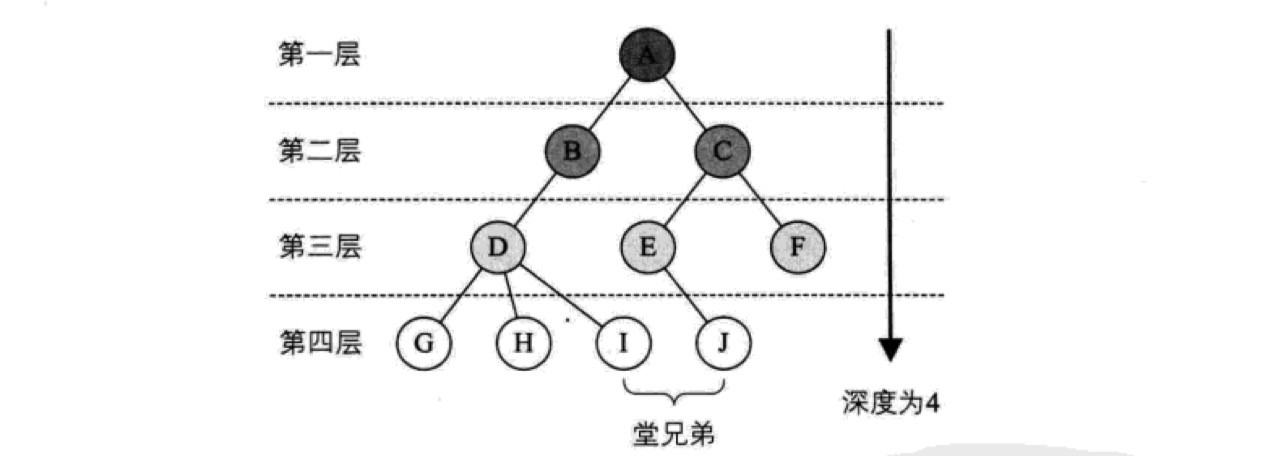
另外,也有些地方将二叉树的深度定义为结点的最大层次数,比如《大话数据结构》就是这样定义的,这个问题不大,完全就是个定义而已:
多个互不相交的树可以构成森林。
二叉树的定义
二叉树是我们平时遇到的最常见的树结构,它是一种特殊的树,顾名思义,就是每个节点最多有两个「分叉」,即两个子节点,分别是左子节点和右子节点,不过,二叉树并不要求每个节点都有两个子节点,有的节点只有左子结点,有的节点只有右子节点。比如下面这些都是二叉树:
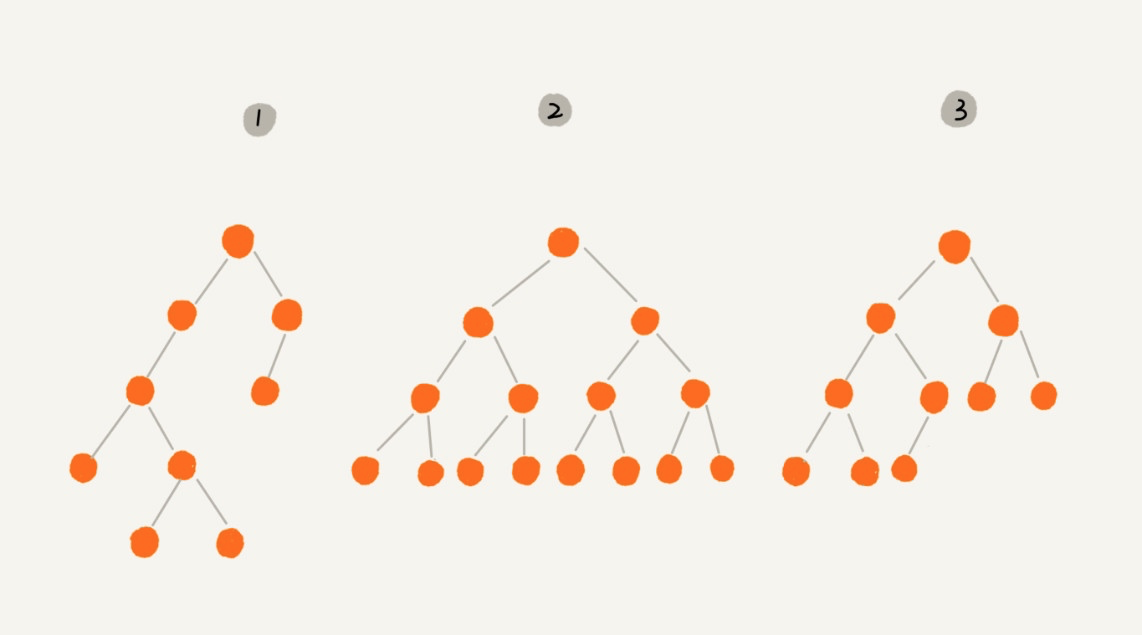
根据左右子节点的饱和度,我们又从二叉树中提取出两种特殊的二叉树 —— 满二叉树和完全二叉树。满二叉树即所有分支节点都有左右子节点,并且所有叶子节点都在同一层上,如上面的图2便是满二叉树。完全二叉树要复杂一些,深度为 k 有 n 个节点的二叉树,当且仅当其中的每一节点,都可以和同样深度 k 的满二叉树,序号为 1 到 n 的节点一对一对应时,称为完全二叉树,比如上面的图3就是完全二叉树。
二叉树的特性
在讨论二叉树的创建和存储之前,我们先来总结下二叉树的一些特性,以便后续用到(这里二叉树数的深度定义采用的最大层次数,如果从 0 开始计算的话,可以自行推演一下)
在第 i 层最多有 2^(i-1) 个节点。
深度为 k 的二叉树最多有 2^k - 1 个节点。
对于任何一个二叉树,叶子节点数为 n0,度为 2 的节点数为 n2,则 n0 = n2+1。


原文:https://www.cnblogs.com/stringarray/p/12749293.html