1.本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性
回顾机器学习分类:监督学习,半监督学习,无监督学习,强化学习
监督学习分为:回归,分类
回归分为:线性回归,Logistic回归
有监督:训练数据集必须是有标记,然后通过给定的训练数据和特定的算法去构造一个模型。
无监督:训练数据集没有标记,去寻找训练数据中隐藏的模式或者是对数据进行分组。
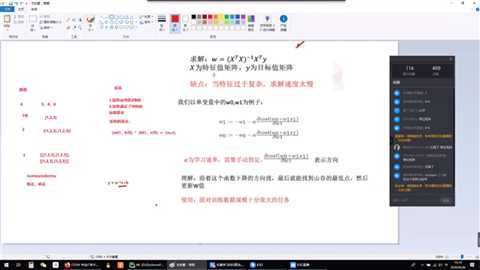
2.思考线性回归算法可以用来做什么?(大家尽量不要写重复)
线性回归算法可以运用在许许多多地方上,比如生活上,我们需要去购物,就能运用该算法,把改价格相近的东西找出来。
3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。(加分题)
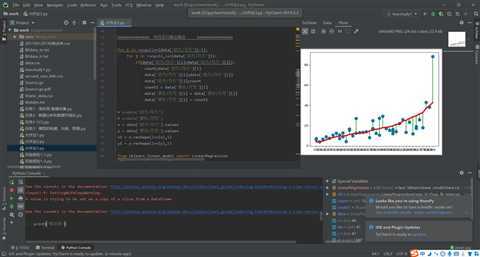
这是上学期做的作业,我预测了汽车的动力与其价格的关系。
print(‘201706120190‘) print(‘陈志炜‘) print(‘软件1702‘) import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.linear_model import LinearRegression data = pd.read_csv(‘201706120190陈志炜.csv‘) data.drop(‘尺寸‘,axis=1,inplace=True) data[‘动力/马力‘] for i in range(len(data[‘动力/马力‘])): data[‘动力/马力‘][i] = data[‘动力/马力‘][i].split(‘马‘)[0] data[‘耗油量/L‘] for i in range(len(data[‘耗油量/L‘])): data[‘耗油量/L‘][i] = data[‘耗油量/L‘][i].split(‘L‘)[0] data[‘尾箱空间/L‘] for i in range(len(data[‘尾箱空间/L‘])): data[‘尾箱空间/L‘][i] = data[‘尾箱空间/L‘][i].split(‘L‘)[0] for i in range(len(data[‘动力/马力‘])-1): for j in range(i,len(data[‘动力/马力‘])): if(data[‘动力/马力‘][i]>data[‘动力/马力‘][j]): count=data[‘动力/马力‘][i] data[‘动力/马力‘][i]=data[‘动力/马力‘][j] data[‘动力/马力‘][j]=count count1 = data[‘原价/万元‘][i] data[‘原价/万元‘][i] = data[‘原价/万元‘][j] data[‘原价/万元‘][j] = count1 # x=data[‘动力/马力‘] # y=data[‘原价/万元‘] x = data[‘动力/马力‘].values y = data[‘原价/万元‘].values x1 = x.reshape(len(x),1) y1 = y.reshape(len(y),1) from sklearn.linear_model import LinearRegression clf = LinearRegression() clf.fit(x1,y1) pre = clf.predict(x1) plt.scatter(x,y,s=100) plt.plot(x,pre,‘r-‘,linewidth=4) for idx, m in enumerate(x): plt.plot([m,m],[y[idx],pre[idx]], ‘g-‘) plt.show()
原文:https://www.cnblogs.com/sgczw/p/12752687.html