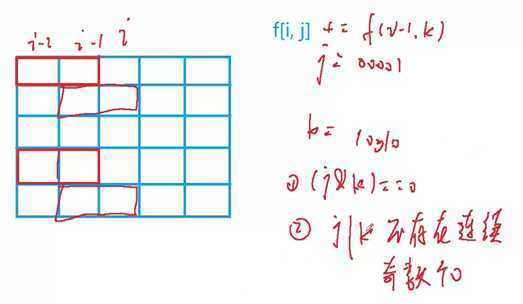
f[i][j]表示第i列上一列横向摆放方格伸出来的方案数
j:本列伸出来的格子的二进制表示。
k:上列伸出来的格子的二进制表示
1)不能有冲突,即1不能有重叠,j & k == 0;
2) 连续的空格不能为奇数,因为横着的已经摆放玩了,只能放竖的了,所以不能有连续奇数个空格,j | k =奇数个0 。 时间复杂度O(n) = 11 * 2^11 * 2^11
#include <iostream> #include <algorithm> #include <cstring> using namespace std; const int N = 12, M = 1 << N; int n, m; unsigned long long f[N][M]; bool st[M]; int main() { int n, m; while(cin>>n>>m, n || m) { memset(f, 0, sizeof f); for(int i = 0; i < 1 << n; i++) { st[i] = true; int cnt = 0; for(int j = 0; j < n; j++) if(i >> j & 1){ if(cnt & 1) st[i] = false; cnt = 0; } else cnt++; if(cnt & 1) st[i] = false; } f[0][0] = 1; for(int i = 1;i <= m; i ++) for(int j = 0; j < 1 << n; j++) for(int k = 0; k < 1 << n; k++) if((j & k) == 0 && st[j | k]) f[i][j] += f[i-1][k]; cout<<f[m][0]<<endl; } }
i >> j & 1 不能打成 i >> j && 1
最短Hamilton路径(旅行商问题)
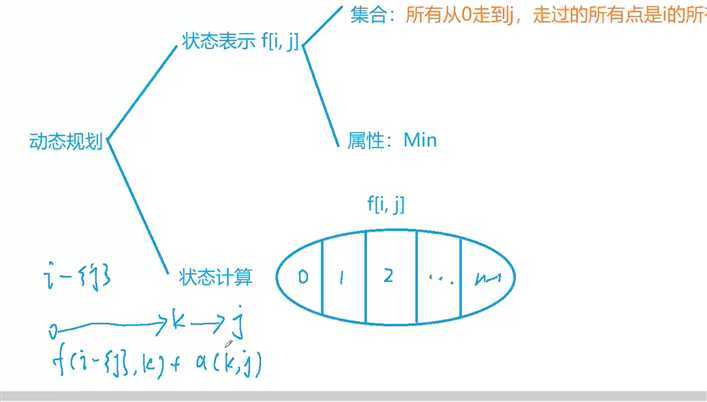
f[i][j] 集合:所有从0走到j,走过的所有点是i的所有路径(110010) 二进制表示
属性:最小值min
状态计算:f[i,j],根据倒数第二点的走法是2
#include <iostream> #include <algorithm> #include <cstring> using namespace std; const int N = 20, M = 1 << N; int n; int w[N][N], f[M][N]; int main() { cin>>n; for(int i = 0; i < n; i++) for(int j = 0; j < n; j ++) cin>>w[i][j]; memset(f, 0x3f, sizeof f); f[1][0] = 0; for(int i = 0; i < 1 << n; i++) for(int j = 0; j < n; j++) if(i >> j & 1) for(int k = 0; k < n; k++) if((i - (1 << j)) >> k & 1) f[i][j] = min(f[i][j], f[i-(1<<j)][k] + w[k][j]); cout<<f[(1 << n) - 1][n-1]<<endl; }
原文:https://www.cnblogs.com/longxue1991/p/12755700.html