虚树(Virtual Tree)指在原树的基础上,选取部分点为 关键点,然后将这些点按照原树上的 父子关系 建树
不难发现,要想要保证 父子关系 不变化,虚树上除了 关键点 以外,还需要有一些关键点的 LCA,我们暂且称之为 LCA点
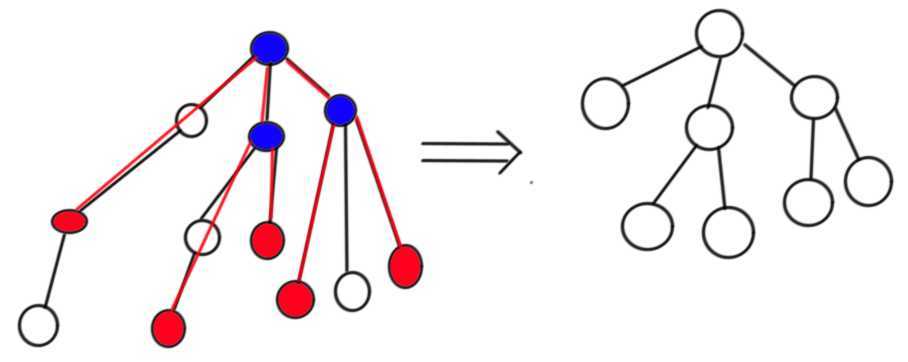
如图,红色点为 关键点,蓝色点是所必须的 LCA点,右图是左图的虚树
这样构建出来的树可以用于剪掉一些不必要的情况
那么怎么建树?
对于一个点 u,如果它的几个儿子的子树中,有大于等于两个儿子的子树中有 key 点,那么这个点,就一定是 LCA点
这个感性理解一下大概挺显然的?
所以只需要一次 DFS,按照上述规则找到所有虚树上的点,再一遍 DFS 来连边即可
以 [SDOI 2019]世界地图 代码为例:

1 bool buildVT(int now, int f) { // 处理出所有虚树点 2 int tot = isKey[now]; 3 // tot 是 自己是否是key点 与 有key点的子树 的数量和 4 for(edge* e = g[now]; e; e = e->next) { 5 int to = e->to; 6 if(to == f) continue; 7 tot += buildVT(to, now); 8 } 9 if(tot >= 2) isKey[now] = 1; 10 return !!tot; 11 } 12 13 // 将上面处理出来的 key 连边形成虚树 14 // last 是上面的那个 key 点, max 是路径上的权值最大值 15 void processVal(int now, int f, int last, int max, std::vector <MSTedge>& V) { 16 if(isKey[now]) { 17 if(last) { 18 V.push_back(MSTedge(now, last, max)); 19 ansdis -= max; 20 } 21 last = now, max = 0; 22 } 23 for(edge* e = g[now]; e; e = e->next) { 24 int to = e->to; 25 if(to == f) continue; 26 processVal(to, now, last, std::max(max, e->val), V); 27 } 28 return; 29 }
复杂度:$O(n)$
原文:https://www.cnblogs.com/Chiaro/p/problem-xiaohaozhan.html