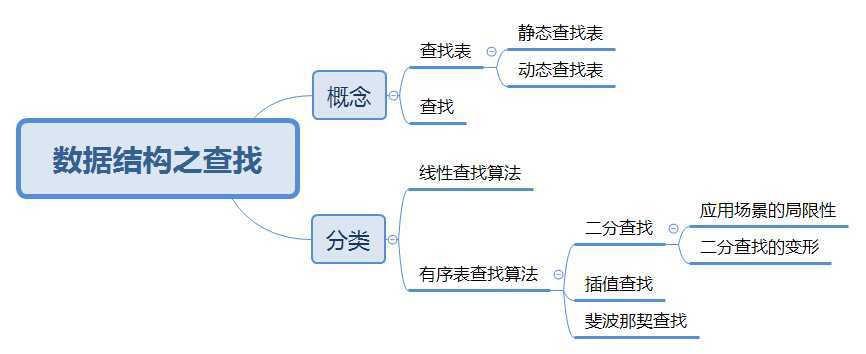
一、基本概念
二、分类
/查找唯一的一个值
public static int searchXian(int[] arr,int value){
for (int i = 0; i < arr.length; i++) {
if (arr[i] == value){
return i;
}
}
return -1;
}
//优化,利用哨兵思想,上述每次都要判断i是否越界,这步操作可以省去
//查找多个相同的值
public static ArrayList<Integer> searchXian11(int[] arr,int value){
ArrayList<Integer> arrayList = new ArrayList<>();
for (int i = 0; i < arr.length; i++) {
if (arr[i] == value){
arrayList.add(i);
}
}
return arrayList;
}
1 //利用递归的方法,数组中不存在重复的元素 2 public static int binarySearch(int[] arr, int low, int high, int value){ 3 //首先low > high ,说明没有找到 4 if(low > high){ 5 return -1; 6 } 7 int mid = (low + high)/2; 8 if(arr[mid] == value){ 9 return mid; 10 }else if(arr[mid] > value){ 11 return binarySearch(arr, low, mid - 1, value); 12 }else{ 13 return binarySearch(arr, mid + 1, high, value); 14 } 15 }
//此时为有序数组,且存在重复的数值,并返回所有的下标。找到mid时,此时不返回,沿mid向两边扫描,将所有的下标值添加到ArrayList集合中
public static ArrayList<Integer> binarySearch1(int[] arr,int low,int high,int findVal){
//定义一个数组集合,用于存放下标
ArrayList<Integer> arrayList = new ArrayList<>();
//当low>high时,说明递归完没有找到值
if (low > high){
return new ArrayList<>();
}
int mid = (low + high)/2;
if (findVal > arr[mid]){
return binarySearch1(arr,mid + 1,high,findVal);//向右递归
}else if(findVal < arr[mid]){
return binarySearch1(arr,low,mid - 1,findVal);//向左递归
}else{
int tempLeft = mid - 1;
int tempRight = mid + 1;
while(arr[tempLeft] == arr[mid] && tempLeft >= 0){
arrayList.add(tempLeft);
tempLeft -= 1;
}
arrayList.add(mid);
while (arr[tempRight] == arr[mid] && tempRight <= arr.length - 1){
arrayList.add(tempRight);
tempRight += 1;
}
return arrayList;
}
}
//非递归方法,数组中不存在重复的元素
public static int binarySearch1(int[] arr,int value){
int low = 0;
int high = arr.length - 1;
while (low <= high){
int mid = (low + high)/2;
if (arr[mid] == value){
return mid;
}else if(arr[mid] > value){
high = mid - 1;
}else{
low = mid + 1;
}
}
return -1;
}
//编写二分查找代码的注意事项:
1.注意结束条件。low <= high
2.注意mid 的取值。(high + low)/2,当high和low 很大时,两者之和容易溢出。可以写成:low + (high - low)/2,若优化到极致的话,可以写为:low + ((high - low)>>1).原因:相比除法运算,计算机的位处理要快很多
3.high和low值的更新
4.O(1)常量级复杂度可能比O(log n)更高。例如:O(300000)和O(log n)相比,后者的执行效率会更高。
//查找第一个值等于给定值的元素
public static int binarySearch3(int[] arr, int value){
int low = 0;
int high = arr.length - 1;
if(low > high){
return -1;
}
while(low <= high){
int mid = low + ((high - low)>>1);
if(arr[mid] = value){
if((arr[mid - 1] != value) || (mid == 0)){
return mid;
}else{
high = mid - 1;
}
}elseif(arr[mid] > value){
high = mid - 1;
}else{
low = mid + 1;
}
}
}
//查找最后一个值等于给定值的元素
public static int binarySearch3(int[] arr, int value){
int low = 0;
int high = arr.length - 1;
if(low > high){
return -1;
}
while(low <= high){
int mid = low + ((high - low) >> 1);
if(arr[mid] = value){
if((arr[mid + 1] != value) || (mid == arr.length - 1)){
return mid;
}else{
low = mid + 1;
}
}elseif(arr[mid] > value){
high = mid - 1;
}else{
low = mid + 1;
}
}
}
//查找第一个大于等于给定值的元素
public static int binarySearch3(int[] arr, int value){
int low = 0;
int high = arr.length - 1;
if(low > high){
return -1;
}
while(low <= high){
int mid = low + ((high - low)>>1);
if(arr[mid] >= value){
if((arr[mid - 1] != value) || (mid == 0)){
return mid;
}else{
high = mid - 1;
}
}else{
low = mid + 1;
}
}
}
//查找最后一个小于等于给定值的元素
public static int binarySearch3(int[] arr, int value){
int low = 0;
int high = arr.length - 1;
if(low > high){
return -1;
}
while(low <= high){
int mid = low + ((high - low)>>1);
if(arr[mid] <= value){
if((arr[mid + 1] != value) || (mid == arr.length - 1)){
return mid;
}else{
low = mid + 1;
}
}else{
high = mid - 1;
}
}
}
原文:https://www.cnblogs.com/zyj-0917/p/12770884.html