一.思维导图

二.重要概念的笔记

1.一般树的存储：

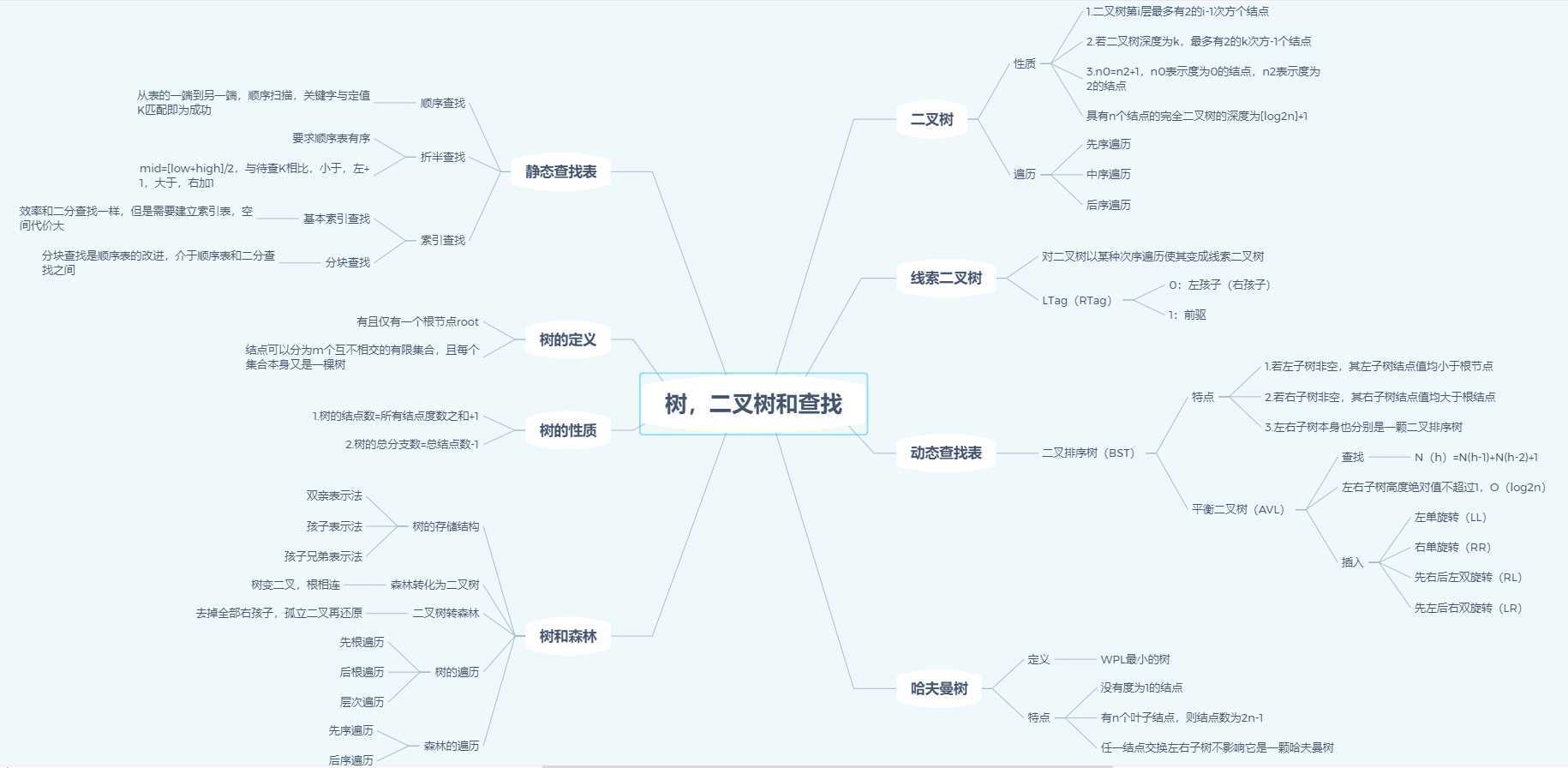
1.双亲表示法：求父节点方便。
2.孩子表示法：求子节点方便。
3.双亲孩子表示法：求父节点和子节点都很方便。
4.二叉树表示法：将一颗普通树转化为二叉树。

2.二叉树的性质：

1.在二叉树的第i层上至多有2^(i-1)个结点（i>0）。
2.深度为k的二叉树至多有2^k-1个结点（k>0）。
3.对于任意一棵二叉树，如果其叶结点为N0，而度数为2的结点总数为N2，则N0=N2+1。
4.具有n个结点的完全二叉树的深度必为 log（2n）+1。
5.对完全二叉树，若从上至下、从左只右编号，则编号为i的节点，其左孩子编号必为2i，其有孩子编号必为2i+1；其双亲的编号必为i/2（i=1时为根 除外）。

3.折半查找的时间复杂度为：O(log2n)。

4.二叉排序树的删除：

1.如果删除的结点没有孩子，则删除后算法结束；
2.如果删除的结点只有一个孩子，则删除后该孩子取代被删除结点的位置；
3.如果删除的结点有两个孩子，则选择该结点的后继结点（该结点右孩子为根的树中的左子树中的值最小的点）或者前驱节点（该结点左孩子为根的树中的右子树中值最大的点）作为新的根，同时在该后继结点或者前驱节点开始，执行前两种删除算法，删除算法结束。

5.哈夫曼树：

带权路径长度最短的树，权值较大的结点离根较近。

6.散列表：

解决冲突方法：
1.开放定址法 – 探测方式：线性探测、二次探测。
2.分离链接法 – 利用链表的方式。

三.疑难问题及解决方案

1.一开始接触二叉平衡树时，对它的构建成一棵树过程比较不理解，在老师讲解后，通过练习现在比较熟练了。

2.6-4 jmu-ds-表达式树 (25分)

void InitExpTree(BTree &T,string str)
{
    stack<BTree> num;
    stack<char> ch;
    int i=0;
    ch.push(‘#‘);
    while(str[i])
    {
        if(!In(str[i]))
        {
            T=new BTNode;
            T->data=str[i];
            i++;
            T->lchild=T->rchild=NULL;
            num.push(T);
        }
        else
        {
            if(Precede(ch.top(),str[i])==‘<‘)
            {
                ch.push(str[i]);
                i++;
            }
            else if(Precede(ch.top(),str[i])==‘=‘)
            {
                ch.pop();
                i++;
            }
            else
            {
                T=new BTNode;
                T->data=ch.top();
                T->rchild=num.top();
                num.pop();
                T->lchild=num.top();
                num.pop();
                num.push(T);
                ch.pop();
            }
        }
    }
    while(ch.top()!=‘#‘)
    {
        T=new BTNode;
        T->data=ch.top();
        T->rchild=num.top();
        num.pop();
        T->lchild=num.top();
        num.pop();
        num.push(T);
        ch.pop();
    }
    T=num.top();
}
double EvaluateExTree(BTree T)
{
    double sum=0,a,b;
    if(!T->lchild&&!T->rchild)
    {
        return T->data-‘0‘;
    }
    a=EvaluateExTree(T->lchild);
    b=EvaluateExTree(T->rchild);
    switch(T->data)
    {
        case‘+‘:
        return a+b;
        case‘-‘:
        return a-b;
        case‘*‘:
        return a*b;
        case‘/‘:
        if(b==0)
        {
            cout<<"divide 0 error!";
            exit(0);
        }
        return a/b;
    }
}

本题一开始并没有太好的思路，在老师的讲解以及百度查询后解了出来

树，二叉树，查找算法总结

原文：https://www.cnblogs.com/b12345/p/12772126.html