NOIP普及组2018 T4 对称二叉树
题目:
一棵有点权的有根树如果满足以下条件,则被轩轩称为对称二叉树:
下图中节点内的数字为权值,节点外的 id 表示节点编号。
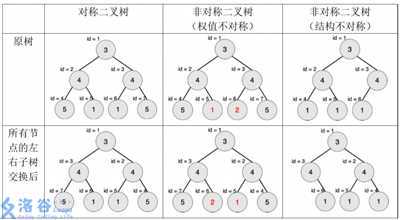
现在给出一棵二叉树,希望你找出它的一棵子树,该子树为对称二叉树,且节点数 最多。请输出这棵子树的节点数。
注意:只有树根的树也是对称二叉树。本题中约定,以节点 T 为子树根的一棵“子 树”指的是:节点T 和它的全部后代节点构成的二叉树。
第一行一个正整数 n,表示给定的树的节点的数目,规定节点编号 1~n,其中节点 1 是树根。
第二行 n 个正整数,用一个空格分隔,第 i 个正整数 vi? 代表节点 i 的权值。
接下来 n 行,每行两个正整数 li, ri?分别表示节点 i 的左右孩子的编号。如果不存在左 / 右孩子,则以 −1 表示。两个数之间用一个空格隔开。
输出文件共一行,包含一个整数,表示给定的树的最大对称二叉子树的节点数。
输入#1
2
1 3
2 -1
-1 -1
输出:1
输入#2
10 2 2 5 5 5 5 4 4 2 3 9 10 -1 -1 -1 -1 -1 -1 -1 -1 -1 2 3 4 5 6 -1 -1 7 8
输出:3
主要题意:
输入题意:首先给定一个n,第一行输入第i个点对应的权值。随后的n行各两个数字,代表这个点的左右节点分别为谁
若没有则用-1表示。
算法目的:要求求出这个树中最大的对称二叉树的结点个数
第一步:分析样例
(由于样例一太水直接分析样例二好了
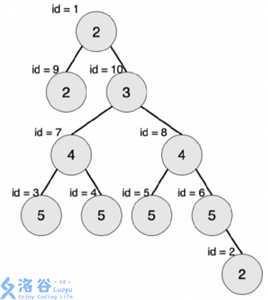
容易发现在这个树中,最大的对称二叉树是
(id=7) 4
(id=3) 5 (id=4)5
第二步:考虑算法
分析完成样例后,考虑我们找到最大二叉树的思考过程
首先我们可以先算出各个子节点所包含的子节点数,这样可以方便我们在找到满足的对称二叉树后直接找到这个对称二叉树包含的节点数。
Part 1代码
int dfs(int point)
{
if(!point)return 0;
else return shu[point]=dfs(le[point])+dfs(ri[point])+1;
}
随后我们便进行这个题的核心代码部分,即是判断满不满足对称性。
其实也很简单,一行一行的遍历是否满足就可以了,若不满足return false,若当前节点满足继续往下搜,若搜到头return true。
Part 2 代码
bool if_ture(int a1,int a2)
{
if(a[a1]!=a[a2])return false;
else if(a1==0&&a2==0)return true;
else return if_ture(le[a1],ri[a2])&&if_ture(ri[a1],le[a2]);
}
剩下的操作就很简单了,综合上面的代码处理并求出最大对称二叉树的节点数。这里可以有一个优化,对于一个点而言,想判断它是否满足
对称二叉树性质,可以先判断它的左右节点所包含的节点数相不相同。显然若不相同,那么我们就算搜也是false,这里是一个小剪枝。
Part 3代码
void deal(int point)
{
if(!point) return;
if(shu[le[point]]==shu[ri[point]])
{
if(if_ture(le[point],ri[point])&&shu[point]>ans)
{
ans=shu[point];
}
}
deal(le[point]),deal(ri[point]);
}
这样对称二叉树这个题就完成啦(撒花撒花)
完整代码如下:
#include<bits/stdc++.h>
#define N 10000007
using namespace std;
int a[N],le[N],ri[N],shu[N],ans;
bool if_ture(int a1,int a2)
{
if(a[a1]!=a[a2])return false;
else if(a1==0&&a2==0)return true;
else return if_ture(le[a1],ri[a2])&&if_ture(ri[a1],le[a2]);
}
int dfs(int point)
{
if(!point)return 0;
else return shu[point]=dfs(le[point])+dfs(ri[point])+1;
}
void deal(int point)
{
if(!point) return;
if(shu[le[point]]==shu[ri[point]])
{
if(if_ture(le[point],ri[point])&&shu[point]>ans)
{
ans=shu[point];
}
}
deal(le[point]),deal(ri[point]);
}
int main()
{
int n;
cin>>n;
for(int i=1;i<=n;i++)cin>>a[i];
for(int i=1;i<=n;i++)
{
cin>>le[i]>>ri[i];
if(le[i]==-1)le[i]=0;
if(ri[i]==-1)ri[i]=0;
}
dfs(1);
deal(1);
cout<<ans;
return 0;
}
(蒟蒻的第一篇题解,如果对在看的dalao有帮助的话可不可给点个赞呢qwq)
原文:https://www.cnblogs.com/gclqwq/p/12775901.html