树、二叉树、查找算法总结

一、思维导图

二、重要概念的笔记

1、树的概念及性质

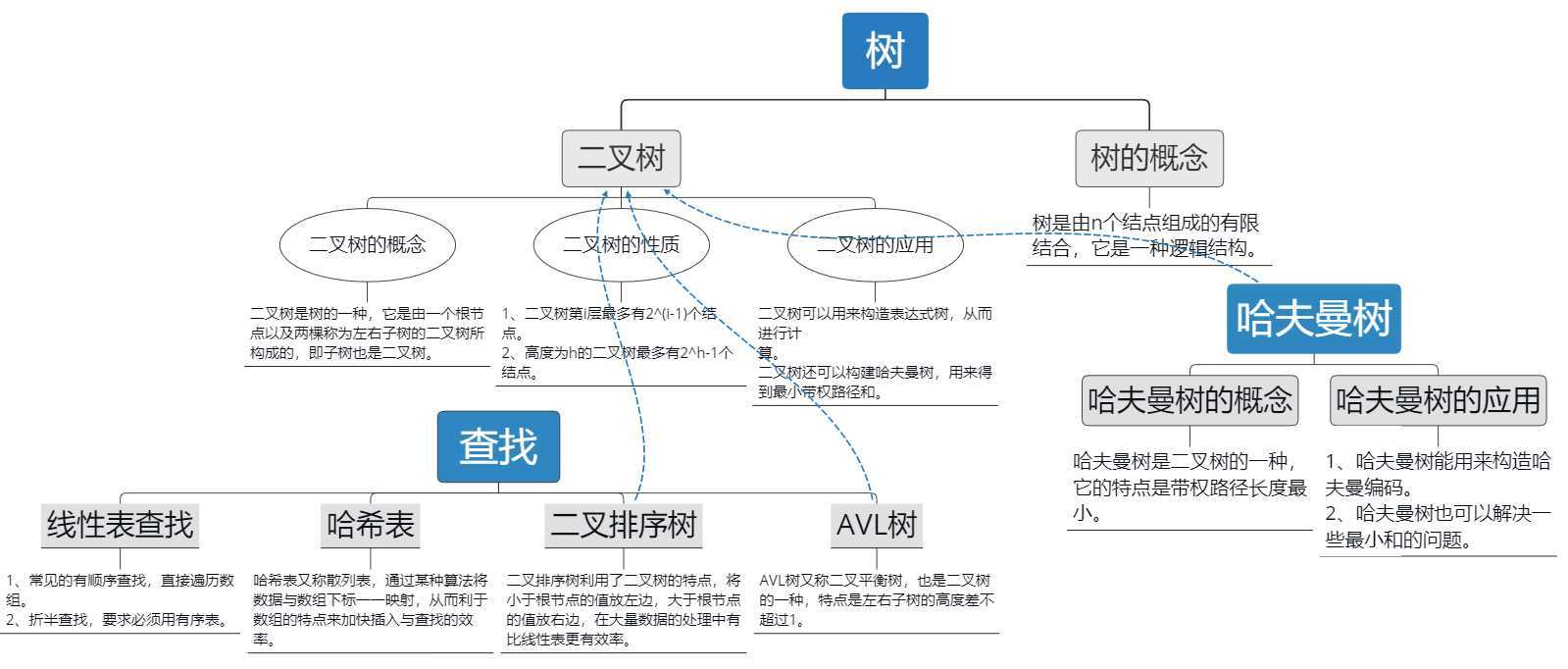
树是逻辑结构的一种，它是由n个结点构成的有限结合。

树的结点的子树个数称为结点的度，而所有结点中度的最大值称为树的度，度为零的结点称为叶子结点。树的总结点数 = 所有结点的度数之和加一。

2、二叉树

二叉树是特殊的树，它的特点是由左右子树的二叉树和根节点组成。可以用顺序或者链式存储来实现。

树的结点是一个结构体，二叉树的结点通常包括数据和指向左右子树的指针。

typedef struct bintree{
	int data;
	bintree*left,*right;
}bintree;

3、二叉树的先、中、后及层序遍历

二叉树是我们所构想的一种树形结构，但是在计算机中，我们很难将这种树形结构直接的显示出来，所以我们常用遍历二叉树的方式来按一定顺序输出它的数据。

先序遍历：

? 二叉树的先序遍历以根左右为原则，先输出结点的值，再访问左右两个结点。通常可以直接用递归来实现

void PreOrder(bintree*bt){
	if(bt){
		cout<<bt->data<<" ";
		PreOrder(bt->left);
		PreOrder(bt->right);
	}
}

中序遍历：

? 中序遍历以左根右为原则，即先访问二叉树的最左子树，再输出其值，然后返回并输出上一个结点的值，一直退回到根节点，接下来访问根节点的右子树，重复以上流程。

void InOrder(bintree*bt){
	if(bt){
		InOrder(bt->left);
		cout<<bt->data<<" ";
		InOrder(bt->right);
	}
}

显然用递归进行中序遍历时，我们只需要将输出语句调换一下位置即可。

后序遍历：

? 后序遍历以左右根为原则进行遍历，将输出语句放在最后即可。

void PostOrder(bintree*bt){
	if(bt){
		PostOrder(bt->left);
		PostOrder(bt->right);
		cout<<bt->data<<" ";
	}
}

层序遍历：
层序遍历是对二叉树进行逐层的遍历，与上述三种遍历使用栈来遍历不同，层序遍历利用队列来实现，下面我们借用数组模拟队列来进行层序遍历。

void Order(bintree*bt){
	bintree*ans[101];
	int head = 0,tail = 0;
	ans[tail++] = bt;
	while(head!=tail){
		bt = ans[head++];
		if(bt){
			cout<<bt->data<<" ";
			ans[tail++] = bt->left;
            ans[tail++] = bt->right;
		}
	}
}

4、哈夫曼树

在许多应用中我们常为树的结点赋予一个具有意义的数值，称为权，利用哈夫曼树，我们可以得到最小带权路径和，以此来解决一些实际问题。

哈夫曼树的本质依然是二叉树，只是哈夫曼树是将最小的两个数据构成一棵二叉树，根结点为两子树的和，然后将其放入集合中，重复上述操作，直到集合中的所有数据构成一棵二叉树，这时候我们就得到了哈夫曼树。

所以，构建哈夫曼树的难点就在于如何得到两个最小结点，如果用普通的数组来实现的话，我们需要不断遍历找出两个最小值，在结点数稍多时便会非常吃力，亦或者先对数据预处理，将其排序，然后每次取出头两个结点，构建完后再用插入排序放入其中，这样的话显然用链式存储会更有效率些，于是，我们可以借用STL库中的优先级队列来实现。

#include <iostream>
#include <queue>
#include <vector>
using namespace std;
int main()
{
	priority_queue<int, vector<int>, greater<int>>ans;
	int n, sum = 0;
	cin >> n;
	for (int i = 0; i < n; i++) {
		int t;
		cin >> t;
		ans.push(t);
	}
	while (ans.size() != 1) {
		int t1 = ans.top();
		ans.pop();
		int t2 = ans.top();
		ans.pop();
		sum = sum + t1 + t2;
		ans.push(t1+t2);
	}
	cout << sum;
	return 0;
}

优先级队列用来求哈夫曼树的解确实十分方便，但在逻辑上并没有构成树形结构，所以，我们也可以尝试利用堆排序来实现哈夫曼树的构建，并且求得带权路径长度的最小值。

#include <stdio.h>
#include <stdlib.h>
typedef struct _heap {
	int weight;
	_heap* left, * right;
}heap;
#define mindata 0
heap* ans[20001];
int anssize = 0;
int anscapacity;
void cre(int x);
void insert(heap* p);
heap* del();
int main()
{
	heap* mini = (heap*)malloc(sizeof(heap));
	mini->left = mini->right = NULL;
	mini->weight = mindata;
	ans[0] = mini;
	int N, x,sum = 0;
	scanf("%d", &N);
	anscapacity = N;
	for (int i = 1; i <= N; i++) {
		scanf("%d", &x);
		cre(x);
	}
	for (; anssize > 1;) {
		heap* p = (heap*)malloc(sizeof(heap));
		p->left = del();
		p->right = del();
		p->weight = p->left->weight + p->right->weight;
		sum += p->weight;
		insert(p);
	}
	heap* bt = del();
	printf("%d", sum);
	return 0;
}
void cre(int x) {
	heap* p = (heap*)malloc(sizeof(heap));
	p->left = p->right = NULL;
	p->weight = x;
	int i = ++anssize;
	for (; ans[i / 2]->weight > x; i /= 2) {
		ans[i] = ans[i / 2];
	}
	ans[i] = p;
}
void insert(heap* p) {
	int i = ++anssize;
	for (; ans[i / 2]->weight > p->weight; i /= 2) {
		ans[i] = ans[i / 2];
	}
	ans[i] = p;
}
heap* del() {
	heap* bt = ans[1];
	heap* tmp = ans[anssize--];
	int parent, child;
	for (parent = 1; parent * 2 <= anssize; parent = child) {
		child = parent * 2;
		if ((child != anssize) && (ans[child]->weight > ans[child + 1]->weight))child++;
		if (ans[child]->weight > tmp->weight)break;
		ans[parent] = ans[child];
	}
	ans[parent] = tmp;
	return bt;

堆排序对比于优先级队列确实比较复杂，但是从逻辑上将堆排序更为符合，同时我们也可以遍历这棵哈夫曼树，还是非常有用的。

5、二叉排序树

二叉排序树算是二叉树中非常有用且常见的一种了，它可以帮助我们提高插入与查找数据的效率。

它的特点是：

? 非空左子树的所有键值小于其根结点的键值。

? 非空右子树的所有键值大于其根结点的键值。

? 左、右子树都是二叉搜索树。

我们可以利用算法来判断一棵二叉树是否为二叉排序树

bool IsMax(BinTree T, int max)
{
    if (!T)
        return true;
    else if (T->Data > max)
        return false;
    return IsMax(T->Left, max) && IsMax(T->Right, max);
}
bool IsMin(BinTree T, int min)
{
    if (!T)
        return true;
    else if (T->Data < min)
        return false;
    return IsMin(T->Left, min) && IsMin(T->Right, min);
}
bool IsBST(BinTree T)
{
    if (!T)
        return true;
    else if (!T->Left  && !IsMax(T->Left, T->Data))
        return false;
    else if (!T->Right && !IsMin(T->Right, T->Data))
        return false;
    return IsBST(T->Left) && IsBST(T->Right);
}

值得一提的是对二叉排序树进行中序遍历就可以得到一个递增的有序序列。

6、查找

我们常用的顺序查找和折半查找

顺序查找：

? 顺序查找就是对数组直接遍历，直到找到要找到的值或者超出数组范围，我们可以在数组中设置一个哨兵来减少每次对是否超限的比较，从而提高效率。

折半查找：

? 折半查找的前提是有序表，每次取中间位与关键值比较，然后改变搜索范围，类似于二叉排序树，通过大小比较来缩小范围，从而提高查找的效率。

? 我们只需要对数组进行预处理，将其排序即可。

AVL树：

? AVL树又叫二叉平衡树，其特点是左右子树高度差不超过1，构建类似于二叉排序树，只是每次都检查左右子树的高度，若高度差大于1，则调整二叉树，从而构建一个平衡的二叉排序树，优点是在遇到类似递增的输入数据时，我们可以通过调整二叉树避免其形成一种线性的逻辑结构，从而保证二叉树的搜索效率。

下面我们模拟一下AVL树的构建：

#include <stdio.h>
#include <stdlib.h>
typedef struct _bi {
	int data;
	int height;
	_bi* left, * right;
}bintree;
int max(int a, int b) {
	return a > b ? a : b;
}
int getheight(bintree* bt) {
	if (!bt)return 0;
	return bt->height;
}
bintree* LL(bintree* bt) {
	bintree* b = bt->left;
	bt->left = b->right;
	b->right = bt;
	bt->height = max(getheight(bt->left), getheight(bt->right)) + 1;
	b->height = max(getheight(b->left), bt->height) + 1;
	return b;
}
bintree* RR(bintree* bt) {
	bintree* b = bt->right;
	bt->right = b->left;
	b->left = bt;
	bt->height = max(getheight(bt->left), getheight(bt->right)) + 1;
	b->height = max(bt->height, getheight(b->right)) + 1;
	return b;
}
bintree* LR(bintree* bt) {
	bt->left = RR(bt->left);
	return LL(bt);
}
bintree* RL(bintree* bt) {
	bt->right = LL(bt->right);
	return RR(bt);
}
bintree* avlinsert(bintree* bt, int x) {
	if (!bt) {
		bt = (bintree*)malloc(sizeof(bintree));
		bt->height = 0;
		bt->data = x;
		bt->left = bt->right = NULL;
	}
	else if (bt->data > x) {
		bt->left = avlinsert(bt->left, x);
		if (getheight(bt->left) - getheight(bt->right) == 2) {
			if (bt->left->data > x)bt = LL(bt);
			else bt = LR(bt);
		}
	}
	else if (bt->data < x) {
		bt->right = avlinsert(bt->right, x);
		if (getheight(bt->right) - getheight(bt->left) == 2) {
			if (bt->right->data < x)bt = RR(bt);
			else bt = RL(bt);
		}
	}
	bt->height = max(getheight(bt->left), getheight(bt->right)) + 1;
	return bt;
}
void pre(bintree* bt) {
	if (bt) {
		
		pre(bt->left);
		printf("%d ", bt->data);
		pre(bt->right);
	}
}
int main()
{
	bintree* bt = NULL;
	int n = 7;
	int a[] = { 31,27,6,67,88,53,15, };
	for (int i = 0; i < n; i++)bt = avlinsert(bt, a[i]);
	printf("hello\n");
	pre(bt);
	return 0;
}

7、哈希表

哈希表是我个人非常喜欢的一种查找方式，它将关键字与数组下标映射，使我们好像能够将关键字作为下标，直接访问数组，以此来进行读取与访问。

哈希表常用的处理一般是除留余数法，我们常将关键字模P来得到地址，即 adr = key%p,这里的p我们常取不大于数据规模n的最大素数。

当然，在对关键字的处理中，我们常会遇到不同关键字在转换后得到同一地址的情况，我们称之为冲突，处理冲突常有三种形式

第一种是线性探测法，通过对该地址的下一个位置不断试探，一直到找到空的位置为止，将其存放。

bool insert(hash* hs, int n) {
	if (find(hs, n))return false;
	int key = n % pre;
	while (hs->key[key] != empty && hs->key[key] != delkey) {
		key = (key + 1) % pre;
	}
	hs->key[key] = n;
	return true;
}

第二种是平方探测法，与线性探测法类似，只不过是以1、-1、4、-4的形式来试探。

第三种是拉链法，我认为是比较实用的方法，因为线性探测法和平方探测法是借助其他地址来存储数据，很容易再次遇到冲突，同时在查找时也较为不便，但拉链法以链式存储结构实现，数据在同一地址中冲突以头插法来存储，所以在查找时我们也只需要遍历该地址的所有指针即可。

#include <stdio.h>
#include <stdlib.h>
#define pre 13
typedef struct _list {
	int data;
	_list* next;
}list;
typedef struct _hash {
	list* first;
}hash;
hash* cre(int maxsize) {
	hash* hs = (hash*)malloc(sizeof(hash) * maxsize);
	for (int i = 0; i < maxsize; i++)hs[i].first = NULL;
	return hs;
}
void insert(hash* hs, int n) {
	list* p = (list*)malloc(sizeof(list));
	p->data = n;
	p->next = NULL;
	int adr = n % pre;
	if (!hs[adr].first)hs[adr].first = p;
	else {
		p->next = hs[adr].first;
		hs[adr].first = p;
	}
}
bool del(hash* hs, int n) {
	int adr = n % pre;
	list* p = hs[adr].first;
	if (!p)return false;
	if (p->data == n) {
		hs[adr].first = p->next;
		free(p);
		return true;
	}
	list* q = p->next;
	while (q && q->data != n) {
		p = q;
		q = q->next;
	}
	if (!q)return false;
	if (q->data == n) {
		p->next = q->next;
		free(q);
	}
	return true;
}
bool find(hash* hs, int n) {
	int adr = n % pre;
	list* p = hs[adr].first;
	if (!p)return false;
	while (p && p->data != n)p = p->next;
	if (p->data == n)return true;
	return false;
}

三、疑难问题及解决方案

问题一：
哈夫曼树的实现是需要我们先得到两个最小的数，使用普通的数组来实现显然非常低效，但是借由堆排序来实现的话代码又比较复杂，在解决问题时容易出错。

解决：

? 根据哈夫曼树的原理，难点就在于得到两个最小数并存取，很容易让人想到可以借助排序的队列来实现，于是我去查了下STL的用法，找到了优先级队列，大大精简了代码，从解决问题的角度上效率比堆排序好多了。

问题二：
哈希表是非常有趣的一种算法，但是在解决问题时，对于哈希函数的选取以及冲突的解决方案实在需要下一番心思，同时哈希表是借由数组实现的，所以在数组填满以后要加入新数据十分不便，用拉链法的话可能会导致某一地址的链表非常巨大，在查找时可能超时。

解决：

? 借助STL的map来实现，map就像字典一样，我们选取关键字，然后存储或者读取关键字对应的数据。相比较于哈希表，map更容易我们上手与应用，也更为简洁。

树、二叉树、查找算法总结

原文：https://www.cnblogs.com/JMU718/p/12776013.html