主成分分析PCA(Principal Component Analysis)是非监督的机器学习方法,广泛应用于数据降维。在许多领域的研究与应用中,往往需要对反映事物的多个变量进行大量的观测,收集大量数据以便进行分析寻找规律。多变量大样本无疑会为研究和应用提供了丰富的信息,但也在一定程度上增加了数据采集的工作量,更重要的是在多数情况下,许多变量之间可能存在相关性,从而增加了问题分析的复杂性,同时对分析带来不便。如果分别对每个指标进行分析,分析往往是孤立的,而不是综合的。盲目减少指标会损失很多信息,容易产生错误的结论。因此需要找到一个合理的方法,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量间存在一定的相关关系,因此有可能用较少的综合指标分别综合存在于各变量中的各类信息。主成分分析与因子分析就属于这类降维的方法。
一.主成分分析思想
PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。它的目标是通过某种线性投影,将高维的数据映射到低维的空间中,并期望在所投影的维度上数据的信息量最大(方差最大),以此使用较少的数据维度,同时保留住较多的原数据点的特性。PCA降维的目的,就是为了在尽量保证“信息量不丢失”的情况下,对原始特征进行降维,也就是尽可能将原始特征往具有最大投影信息量的维度上进行投影。将原特征投影到这些维度上,使降维后信息量损失最小。
二,主成分分析求解步骤
求解步骤如下:
假设有M个样本{X1,X2,...,XM},每个样本有N维特征 Xi=(xi1,xi2,...,xiN)T,每一个特征xjxj?都有各自的特征值。
第一步:对所有特征进行中心化:去均值。
求每一个特征的平均值,然后对于所有的样本,每一个特征都减去自身的均值。经过去均值处理之后,原始特征的值就变成了新的值,在这个新值基础上,进行下面的操作。
第二步:求协方差矩阵C(以二维特征为例)
计算公式:
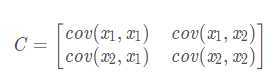
上述矩阵中,对角线上分别是特征x1和x2的方差,非对角线上是协方差。协方差大于0表示x1和x2 ?若有一个增,另一个也增;小于0表示一个增,一个减;协方差为0时,两者独立。协方差绝对值越大,两者对彼此的影响越大,反之越小。其中,cov(x1,x1)的求解公式如下,其他类似。
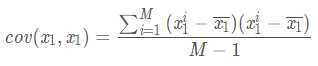
根据上面的协方差计算公式我们就得到了这M个样本在这N维特征下的协方差矩阵C。之所以除以M-1而不是除以M,是因为这样能使我们以较小的样本集更好的逼近总体的标准差,即统计上所谓的“无偏估计”。
第三步:求协方差矩阵C的特征值和相对应的特征向量。
利用矩阵的知识,求协方差矩阵 C 的特征值 λ 和相对应的特征向量 u(每一个特征值对应一个特征向量):Cu=λu
特征值λ会有N个,每一个λi?对应一个特征向量 ui?,将特征值λ按照从大到小的顺序排序,选择最大的前k个,并将其相对应的k个特征向量拿出来,我们会得到一组{(λ1,u1),(λ2,u2),...,(λk,uk)}。
第四步:将原始特征投影到选取的特征向量上,得到降维后的新K维特征
这个选取最大的前k个特征值和相对应的特征向量,并进行投影的过程,就是降维的过程。对于每一个样本$ Xi$,原来的特征是$(xi_1,xi_2,…,xi_n)^T$,投影之后的新特征是 (yi1,yi2,...,yik)T,新特征的计算公式如下:
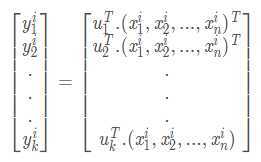
三,PCA优缺点
优点:
1、以方差衡量信息的无监督学习,不受样本标签限制。
2、由于协方差矩阵对称,因此k个特征向量之间两两正交,也就是各主成分之间正交,正交就肯定线性不相关,可消除原始数据成分间的相互影响
3. 可减少指标选择的工作量
4.用少数指标代替多数指标,利用PCA降维是最常用的算法
5. 计算方法简单,易于在计算机上实现。
缺点:
1、主成分解释其含义往往具有一定的模糊性,不如原始样本完整
2、贡献率小的主成分往往可能含有对样本差异的重要信息,也就是可能对于区分样本的类别(标签)更有用
3、特征值矩阵的正交向量空间是否唯一有待讨论
4、无监督学习
四,Python代码实现
原文:https://www.cnblogs.com/mindy-snail/p/12777140.html