树 二叉树 查找算法总结

一. 思维导图

树和二叉树

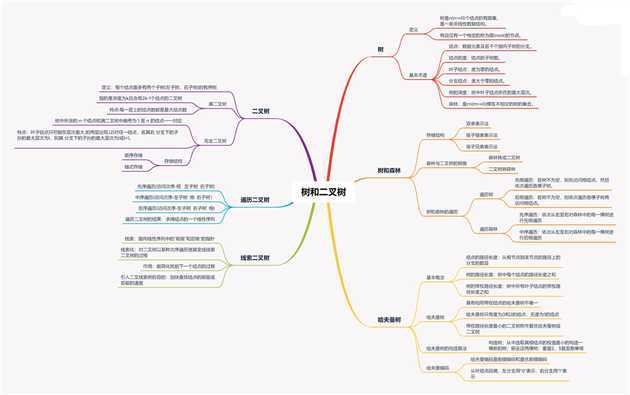
查找

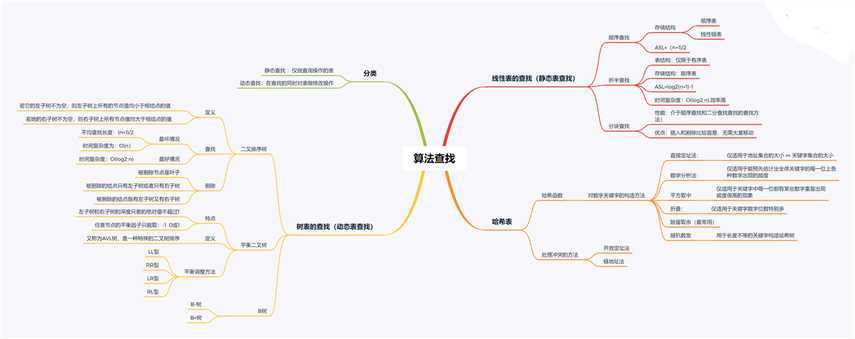
二. 重要概念笔记

1.树的基本操作：

(1).查找

Root(T) //求树的根结点
Value(T,cur_e) //求当前结点的元素值
Parent(T, cur_e) //求当前结点的双亲结点
LeftChild(T, cur_e) //求当前结点的最左孩子 
RightSibling(T, cur_e)//求当前结点的右兄弟 
TreeEmpty(T) // 判定树是否为空树 
TreeDepth(T) // 求树的深度
TraverseTree( T) // 遍历

(2).插入

InitTree(&T) // 初始化置空树
CreateTree(&T, definition)// 按定义构造
Assign(T, cur_e, value) // 给当前结点赋值
InsertChild(&T, &p, i, c)// 将以c为根的树 插入为结点p的第i棵子树

(3).删除

ClearTree(&T) //将树清空 
DestroyTree(&T) //销毁树的结构
DeleteChild(&T,&p,i)//删除结点p的第i个孩子

2.树最适合用来表示【元素之间具有分支层次关系的数据】。

3.树的相关性质：

（1)? 树中的结点数 = 所有结点的度数+1；度数之和=分支数之和；分支数=结点数-1.

(2)? 度为m的树中，第i层上至多有m^i-1个结点（i>=1).

4.二叉树的性质：

性质一：在二叉树的第 i 层上至多有2i-1 个结点(i≥1)

性质二：深度为 k 的二叉树上至多含 2k-1 个结 点(k≥1)

性质三：对于任何一个二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。

性质四：具有n个结点的完全二叉树的深度为[log2n] +1

性质五：对于具有n个结点的完全二叉树，如果按照从上到下从左至右的顺序对所有结点从0开始编号，则对于序号为i的结点有：

(1)若i>0,双亲序号：(i-1)/2;i=0，i为根节点编号，无双亲结点 (2)若2i+1<n,左孩子序号：2i+1，否则无左孩子 (3)若2i+2<n,右孩子序号：2i+2,否则无右孩子

5.两类特殊的二叉树：

(1)满二叉树：

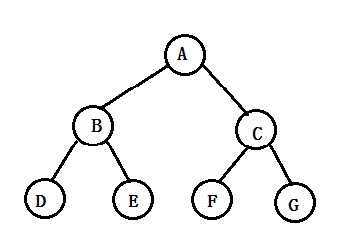
(2)完全二叉树：

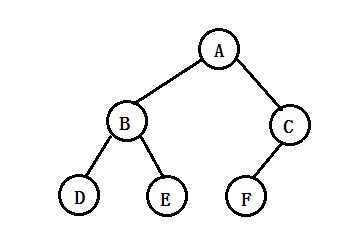
6.二叉树的存储结构：

存储结构:

特点：一组地址连续的存储单元存储各结点(如一维数组)；自根而下、自左而右存储结点; 按完全二叉树上的结点位置进行编号和存储。

缺点：空间利用率太低。

链式存储：

二叉链表

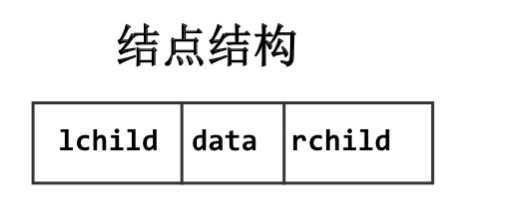
三叉链表

7.遍历二叉树：

先序遍历算法的递归描述:(其余随之变即可）

void Preorder (BiTree T) { //先序遍历二叉树
    if (T) {
            cout<<T->data; // 访问结点 
            Preorder(T->lchild); // 遍历左子树 
            Preorder(T->rchild); // 遍历右子树
     } 
}

8.若x是二叉中序线索树中的一个有左孩子结点，且x不为根，则x的前驱是x的左子树中的最右结点。

9.对树的访问没有中根遍历。

10.树的后根遍历与对应二叉树的中根遍历顺序是一致的。

11.二叉排序树的插入：

插入的元素一定在叶结点上，若二叉排序树为空，则插入结点应为根结点，否则，继续在其左右子树上查找。

12.删除：

被删除的结点是叶子：1）其双亲结点中相应指针域的值改为“空” 2）被删除的结点只有左子树或者只有右子树：其双亲结点的相应指针域的值改为“指向被删除结点的左子树 或右子树” 3）被删除的结点既有左子树，也有右子树：以其直接前驱(后继)替代之，然 后再删除该前驱(后继)结点。

13.二叉排序树的查找性能分析：

平均查找长度和二叉树的形态有关，即，最好：log2n 最坏：(n+1)/2(单支树）

14.对于一棵有n个结点的AVL树，其高度保持在O(log2n)数量级，ASL也保持在O(log2n)量级

15.B-树(多路平衡查找树）

m阶B-树的结点的特点：非根结点:孩子个数 至少: [m/2](向上取整）最多:m

非根结点:关键字个数:至少: [m/2] -1(向上取整） 最多:m-1 根节点至少2个孩子节点

16.B-树的查找：

查到某个叶结点，若相应指针为空，落入一个外部节点，表示查找失败

17.B-树的插入:

在查找不成功之后，需进行插入。关键字插入的位置必定在叶子结点层，有下列几种情况:插入后，该结点的关键字个数n<m-1，不修改指针;插入后，该结点的关键字个数 n=m-1，则需进行"结点分裂“。

18.B+树的查找：

直接从最小关键字开始进行顺序查找所有叶节点链接成的线性链表。从B+树的根节点出发一直找到叶节点为止。

三.疑难问题及解决方法

问题：平衡二叉树的构造， 解决方法：多做题，回看课堂视频。

树 二叉树 算法查找

原文：https://www.cnblogs.com/zghh/p/12769215.html