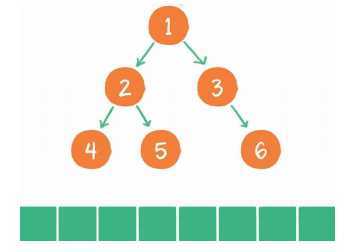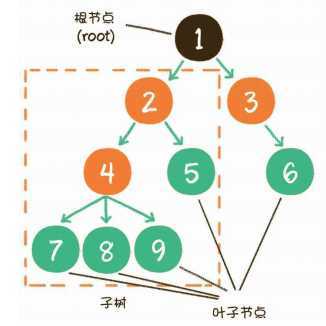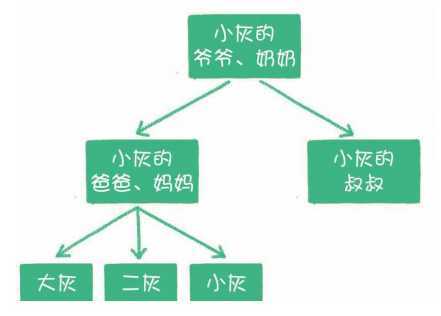
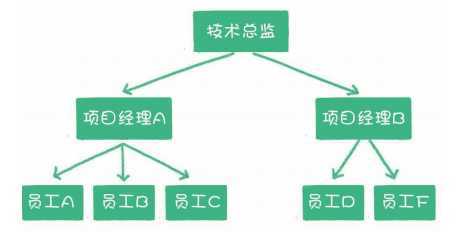
或者企业里的职级关系
又比如一本书的目录
常用树
二叉树
概念
二叉树(binary tree)是树的一种特殊形式。二叉,顾名思义,这种树的每个节点最多有2个孩子节点。注意,这里是最多有2个,也可能只有1个,或者没有孩子节点。
二叉树的结构如图所示:
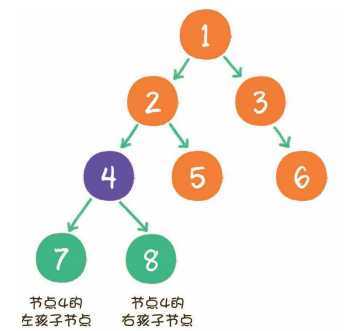
二叉树节点的两个孩子节点,一个被称为左孩子(left child),一个被称为右孩子(right child)。这两个孩子节点的顺序是固定的,就像人的左手就是左手,右手就是右手,不能够颠倒或混淆。
分类
1、满二叉树(完美二叉树)
概念:一个二叉树的所有非叶子节点都存在左右孩子,并且所有叶子节点都在同一层级上,那么这个树就是满二叉树。
图示:
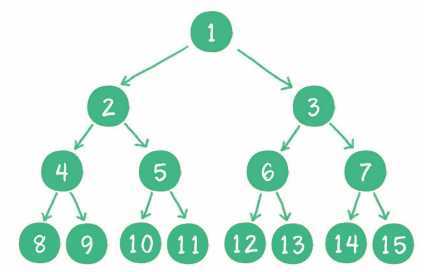
2、完全二叉树
概念:若设二叉树的深度为k,除第 k 层外,其它各层 (1~k-1) 的结点数都达到最大个数,第k 层所有的结点都连续集中在最左边,这就是完全二叉树。
图示:
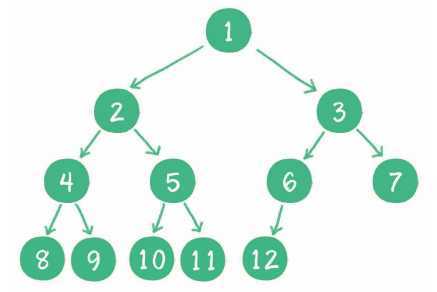
3、平衡二叉树
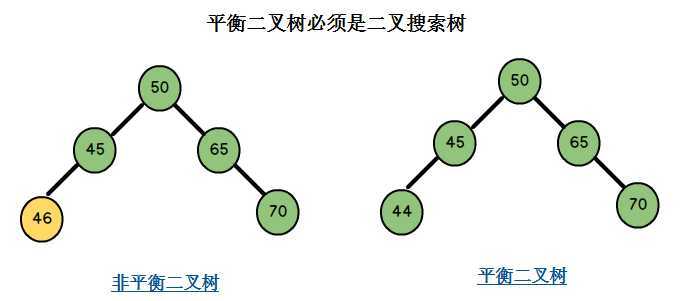
概念:它或者是一颗空树,或它的左子树和右子树的深度之差(平衡因子)的绝对值不超过1,且它的左子树和右子树都是一颗平衡二叉树。
图示:
二叉树存储
二叉树在内存中是怎样存储的呢?
数据结构可以划分为物理结构和逻辑结构。二叉树属于逻辑结构,它可以通过多种物理结构来表达。
二叉树可以用哪些物理存储结构来表达呢?
1. 链式存储结构。
2. 数组。
链式存储
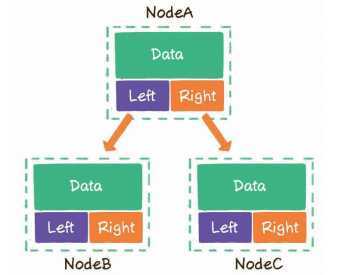
一个节点最多可以指向左右两个孩子节点,所以二叉树的每一个节点包含3部分。
- 存储数据的data变量
- 指向左孩子的left指针
- 指向右孩子的right指针
数组存储
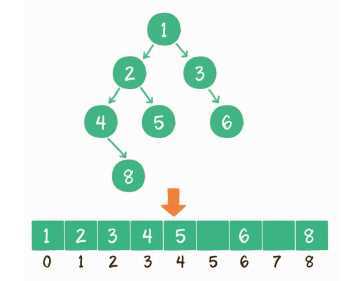
使用数组存储时,会按照层级顺序把二叉树的节点放到数组中对应的位置上。如果某一个节点的左孩子或右孩子空缺,则数组的相应位置也空出来。为什么这样设计呢?因为这样可以更方便地在数组中定位二叉树的孩子节点和父节点。假设一个父节点的下标是parent,那么它的左孩子节点下标就是2×parent + 1;右孩子节点下标就是2×parent + 2。反过来,假设一个左孩子节点的下标是leftChild,那么它的父节点下标就是(leftChild-1)/ 2。假如节点4在数组中的下标是3,节点4是节点2的左孩子,节点2的下标可以直接通过计算得出。节点2的下标 = (3-1)/2 = 1显然,对于一个稀疏的二叉树来说,用数组表示法是非常浪费空间的。
二叉树应用
查找
非常适合查找的树-----二叉查找树(Binary Search)
概念:二叉查找树在二叉树的基础上增加了以下几个条件:
- 如果左子树不为空,则左子树上所有节点的值均小于根节点的值
- 如果右子树不为空,则右子树上所有节点的值均大于根节点的值
- 左、右子树也都是二叉查找树
图示:
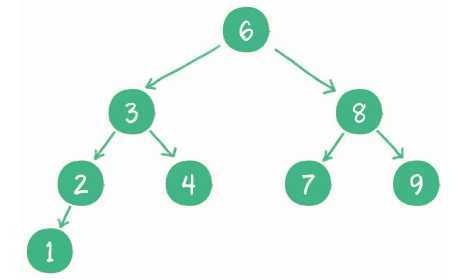
在原本二叉树的基础上增加这些条件又会带来什么样的效果呢?
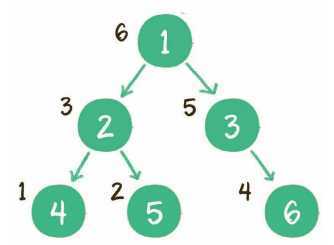
例如查找值为4的节点,步骤如下。
1. 访问根节点6,发现4<6。
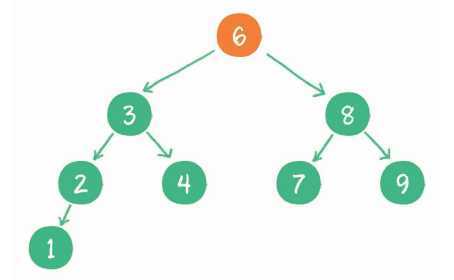
2. 访问节点6的左孩子节点3,发现4>3。
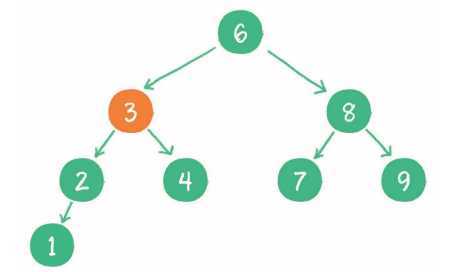
3. 访问节点3的右孩子节点4,发现4=4,这正是要查找的节点。
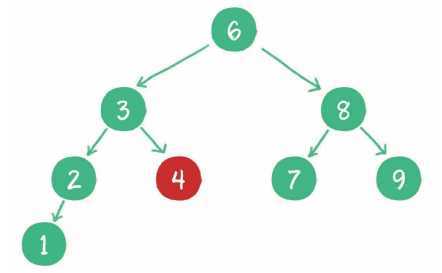
对于一个节点分布相对均衡的二叉查找树来说,如果节点总数是n,那么搜索节点的时间复杂度就是O(logn),和树的深度是一样的。
维持相对顺序
二叉查找树要求左子树小于父节点,右子树大于父节点,正是这样保证了二叉树的有序性。因此二叉查找树还有另一个名字——二叉排序树(binary sort tree)。新插入的节点,同样要遵循二叉排序树的原则。例如插入新元素5,由于5<6,5>3,5>4,所以5最终会插入到节点4的右孩子位置。
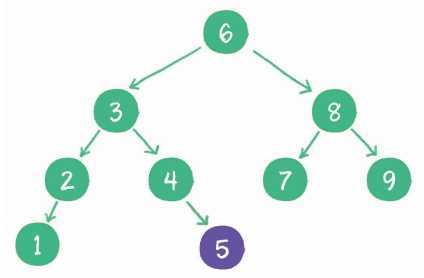
再如插入新元素10,由于10>6,10>8,10>9,所以10最终会插入到节点9的右孩子位置。
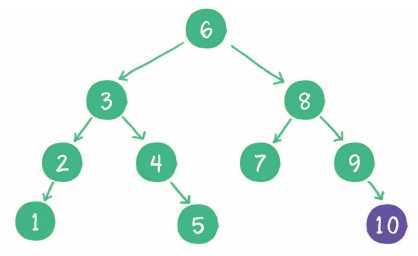
但是二叉查找树也会存在一个问题,例如:
在二叉查找树中依次插入9、8、7、6、5、4
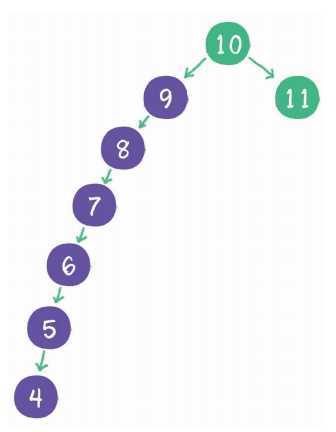
查询节点的时间复杂度也退化成了O(n)。
二叉树遍历
遍历方式
从节点之间位置关系的角度来看,二叉树的遍历分为4种。
- 前序遍历-----根结点-->左子树-->右子树
- 中序遍历-----左子树-->根结点-->右子树
- 后序遍历-----左子树-->右子树-->根结点
- 层序遍历
从更宏观的角度来看,二叉树的遍历归结为两大类。
- 深度优先遍历(前序遍历、中序遍历、后序遍历)
- 广度优先遍历(层序遍历)
深度优先遍历
概念:所谓深度优先,顾名思义,就是偏向于纵深,“一头扎到底”的访问方式。
前序遍历
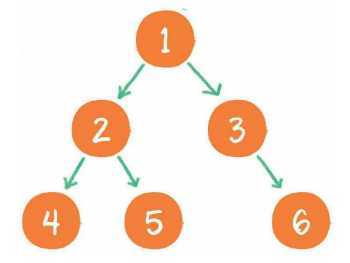
二叉树的前序遍历,输出顺序是根节点、左子树、右子树。
示例:
1. 首先输出的是根节点1。
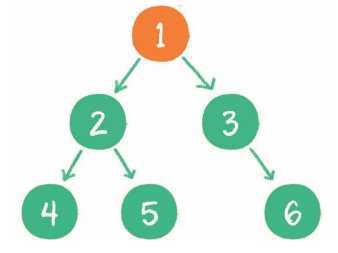
2. 由于根节点1存在左孩子,输出左孩子节点2。
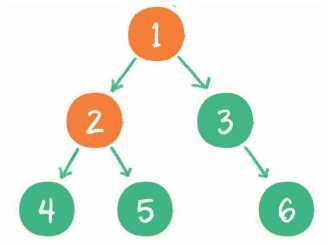
3. 由于节点2也存在左孩子,输出左孩子节点4。
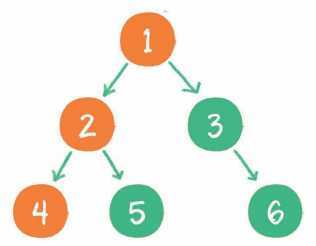
4. 节点4既没有左孩子,也没有右孩子,那么回到节点2,输出节点2的右孩子节点5。
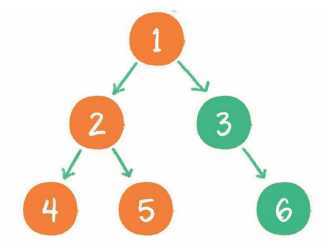
5. 节点5既没有左孩子,也没有右孩子,那么回到节点1,输出节点1的右孩子节点3。
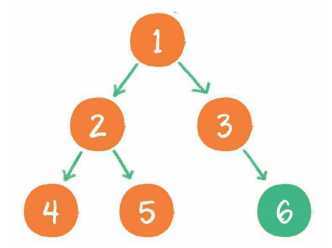
6. 节点3没有左孩子,但是有右孩子,因此输出节点3的右孩子节点6。
中序遍历
二叉树的中序遍历,输出顺序是左子树、根节点、右子树。
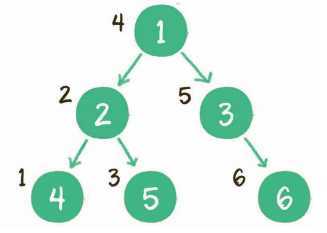
1. 首先访问根节点的左孩子,如果这个左孩子还拥有左孩子,则继续深入访问下去,一直找到不再有左孩子的节点,并输出该节点。显然,第一个没有左孩子的节点是节点4。
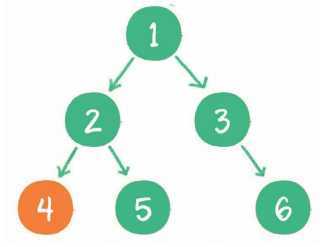
2. 依照中序遍历的次序,接下来输出节点4的父节点2。
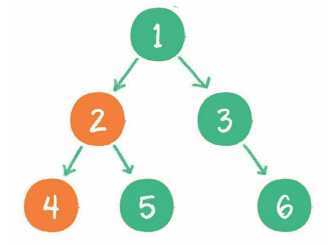
3. 再输出节点2的右孩子节点5。
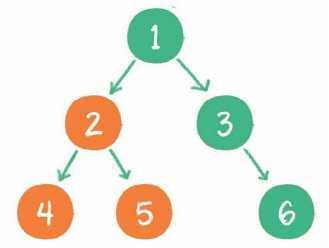
4. 以节点2为根的左子树已经输出完毕,这时再输出整个二叉树的根节点1。
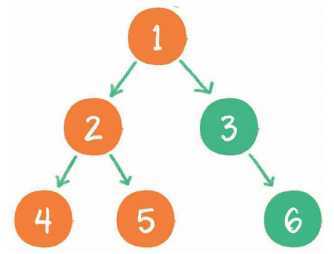
5. 由于节点3没有左孩子,所以直接输出根节点1的右孩子节点3。
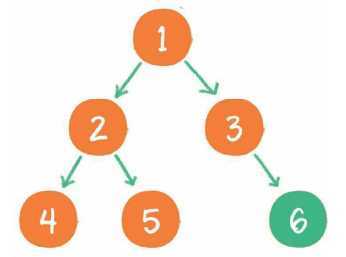
6. 最后输出节点3的右孩子节点6。
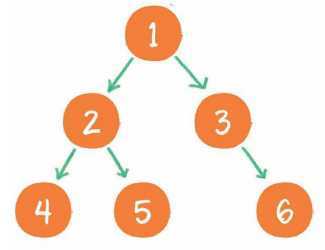
后序遍历
二叉树的后序遍历,输出顺序是左子树、右子树、根节点。
广度优先遍历
其基本思想是尽最大程度辐射能够覆盖的节点,并对其进行访问。
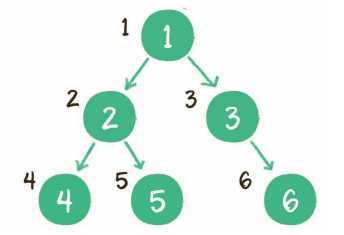
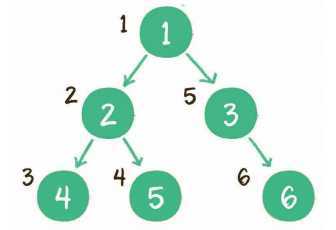
上图就是一个二叉树的层序遍历,每个节点左侧的序号代表该节点的输出顺序。可是,二叉树同一层次的节点之间是没有直接关联的,如何实现这种层序遍历呢?这里同样需要借助一个数据结构来辅助工作,这个数据结构就是队列。
1. 根节点1进入队列。
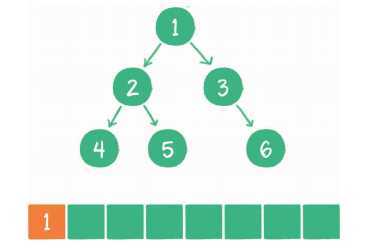
2. 节点1出队,输出节点1,并得到节点1的左孩子节点2、右孩子节点3。让节点2和节点3入队。
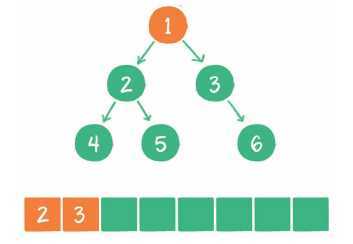
3. 节点2出队,输出节点2,并得到节点2的左孩子节点4、右孩子节点5。让节点4和节点5入队。
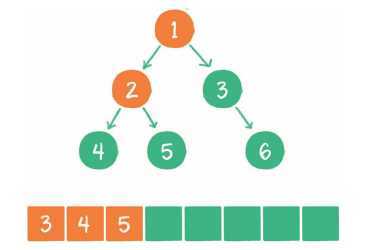
4. 节点3出队,输出节点3,并得到节点3的右孩子节点6。让节点6入队。
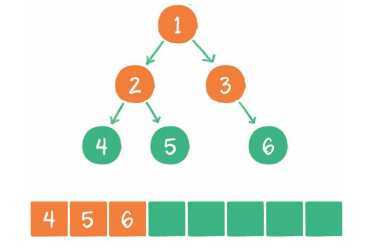
5. 节点4出队,输出节点4,由于节点4没有孩子节点,所以没有新节点入队。
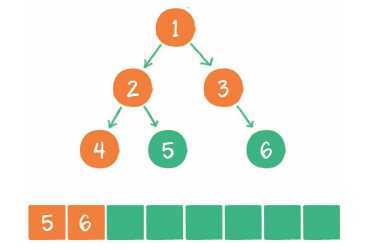
6. 节点5出队,输出节点5,由于节点5同样没有孩子节点,所以没有新节点入队。
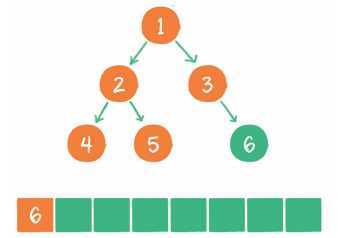
7.节点6出队,输出节点6,节点6没有孩子节点,没有新节点入队。