opengl算法学习--直线绘制
DDA方法
DDA方法(Digital Differential Analyzer)是一种线段扫描转换算法,在一个坐标轴上以单位间隔对线段取样,从而确定另一个坐标轴上最靠近线路径的对应整数值。
方法概述
假设已知直线两端点\(A(x_{a},y_{a})\),\(B(x_{b},y_{b})\)
\(\Delta x=x_{b}-x_{a}\) \(\Delta y=y_{b}-y_{a}\)
已知直线的斜截式方程为y=m* x+b (\(m=\frac{\Delta y}{\Delta x}\))
当\(m\in(0,1)\)时,以单位x间隔(\(\delta x=1\)),逐次计算y值
\[y_{k+1}=y_{k}+m
\]
当\(m\in(1,\infty)\)时,以单位y间隔(\(\delta y=1\)),逐次计算x值
\[x_{k+1}=x_{k}+\frac{1}{m}
\]
对计算出的x与y,要经过四舍五入后置入像素位置
如斜率m<0时,可以通过取m绝对值,从终点向起点绘制
代码实现
DDA算法利用光栅特性消除了直线方程中的乘法,通过在x或y方向使用合适的增量,从而沿线路径逐步得到各像素的位置。但由于浮点增量的存在,使得该方法对于长线段存在较大误差,且浮点运算耗时也相对较大
Bresenham画线算法
Bresenham画线算法是应用最广泛的直线生成算法,它采用加减与乘2运算(即移位运算)来实现。
举例说明,对于一条斜率为\(m\in (0,1)\)的直线,可以预测到在原点的基础上的下一个绘制点,必定为T或者S,因此,可以通过比较TS两点对直线的纵向距离t与s,来确定下一个绘制点
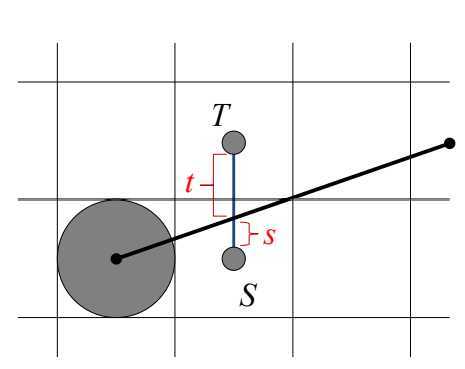
方法概述
当\(m\in(0,1)\)时,选取x轴为计步方向
设原点为( \(x_{i}\) , \(y_{i}\) ),则S( \(x_{i+1}\) , \(y_{i}\) ),T( \(x_{i+1}\) , \(y_{i+1}\) )
\[\because x_{i+1}=x_{i}+1
\]
\[\therefore y=mx_{i+1}+b=m(x_{i}+1)+b
\]
\[s-t=(y-y_{i})-(y_{i+1}-y)
\]
\[\;\;\;\;=y-y_{i}-y_{i}-1+y
\]
\[=2y-2y_{i}-1
\]
\[=2m(x_{i}+1)+2b-2y_{i}-1
\]
\[\because m=\frac{\Delta y}{\Delta x}
\]
\[\therefore \Delta x(s-t)=2\Delta y(x_{i}+1)+\Delta x(2b-2y_{i}-1)
\]
\[=2\Delta y x_{i}-2\Delta x y_{i}+2\Delta y+\Delta x(2b-1)
\]
令
\[d_{i}=\Delta x(s-t)
\]
\[C=2\Delta y+\Delta x(2b-1)
\]
可得
\[d_{i}=2\Delta y x_{i}-2\Delta x y_{i}+C
\]
\[\Rightarrow d_{i+1}=2\Delta y x_{i+1}-2\Delta x y_{i+1}+C
\]
\[=2\Delta y (x_{i}+1)-2\Delta x y_{i+1}+C
\]
\[=2\Delta y x_{i}+2\Delta y+2\Delta x y_{i}-2\Delta x y_{i}-2\Delta x y_{i+1}+C
\]
\[=d_{i}+2\Delta y-2\Delta x(y_{i+1}-y_{i})
\]
当\(d_{i}\)>0时 \(y_{i+1}=y_{i}+1\)
当\(d_{i}\)<0时 \(y_{i+1}=y_{i}\)
\[d_{i+1}=
\left\{\begin{matrix}
d_{i}+2\Delta y-2\Delta x & d_{i}>0 \ d_{i}+2\Delta y & d_{i}\leq 0
\end{matrix}\right.
\]
当i=1时,\(y_{i}=mx_{i}+b\)
所以
\[s-t=2m(x_{i}+1)+2b-2(mx_{i}b)-1
\]
\[=2m-1
\]
\[\Rightarrow d_{1}=\Delta x(s-t)=\Delta x(2m-1)=2\Delta y-\Delta x
\]
当\(m\in(1,\infty)\)时,选取y轴为计步方向
设原点为( \(x_{i}\) , \(y_{i}\) ),则S( \(x_{i+1}\) , \(y_{i}\) ),T( \(x_{i+1}\) , \(y_{i+1}\) )
令k=\frac{1}{m}
\[\because y_{i+1}=y_{i}+1
\]
\[\therefore x=k(y_{i+1}-b)=k(y_{i}+1-b)
\]
\[s-t=(x-x_{i})-(x_{i+1}-x)
\]
\[\;\;\;\;=x-x_{i}-x_{i}-1+x
\]
\[=2x-2x_{i}-1
\]
\[=2k(y_{i}+1)-2kb-2x_{i}-1
\]
\[\because m=\frac{\Delta x}{\Delta y}
\]
\[\therefore \Delta y(s-t)=2\Delta x(y_{i}+1)-2\Delta yx_{i}-2\Delta ykb-\Delta y
\]
\[=2\Delta x y_{i}-2\Delta y x_{i}+2\Delta x-\Delta y(2kb+1)
\]
令
\[d_{i}=\Delta y(s-t)
\]
\[C=2\Delta x-\Delta y(2kb+1)
\]
可得
\[d_{i}=2\Delta x y_{i}-2\Delta y x_{i}+C
\]
\[\Rightarrow d_{i+1}=2\Delta x y_{i+1}-2\Delta y x_{i+1}+C
\]
\[=d_{i}+2\Delta x-2\Delta y(x_{i+1}-x_{i})
\]
当\(d_{i}\)>0时 \(x_{i+1}=x_{i}+1\)
当\(d_{i}\)<0时 \(x_{i+1}=x_{i}\)
\[d_{i+1}=
\left\{\begin{matrix}
d_{i}+2\Delta x-2\Delta y & d_{i}>0 \ d_{i}+2\Delta x & d_{i}\leq 0
\end{matrix}\right.
\]
当i=1时,\(x_{i}=k(y_{i}-b)\)
所以
\[s-t=2k(y_{i}+1)-2kb-2k(y_{i}-b)-1
\]
\[=2k-1
\]
\[\Rightarrow d_{1}=\Delta y(s-t)=\Delta y(2k-1)=2\Delta x-\Delta y
\]
当m<0时,可视为反向绘制,因此适用上式
代码实现
Bresenham画线算法相比DDA算法,因为没有浮点运算,因此更加效率

opengl算法学习---直线绘制
原文:https://www.cnblogs.com/springfield-psk/p/12779584.html

