
概念:树是非线性结构,元素间属于一对多的关系,树是由n个结点(n>=0)个结点构成的有限集合。
基本术语:
结点:数据元素+若干指向子树的分支。
结点的度:分支的个数。
树的度:树中所有结点的度的最大值。
叶子结点:度为0的结点。
分支结点:度大于0的结点。
树的深度:树中叶子结点所在的最大层次。
森林:m(m>0)棵互不相交的树的集合。
性质:
1.树中结点数等于所有结点的度数加1.
2.度为m的树的第i层最多有m^(i-1)(i>=1)个节点.
3.高度为h的m次数最多有(m^h-1)/(m-1)个节点.
4.具有n个节点的m次树的最小高度为?logm (n(m-1)+1)?.
遍历:
1.先根遍历:若树不为空,则先访问根节点,然后依次先根遍历各个子树。
2.后根遍历:若树不为空,则依次后根遍历各个子树,然后访问根节点。
3.层次遍历:若树不为空,则自上而下自左往右访问树中每个节点。
概念:由一个根节点,和两棵互不相交的左右子树组成。
性质:
1.在二叉树的第i层上组多有2^(i-1)个节点(i>=1)。
2.深度为h的二叉树最多含有2^h-1个节点。
3.n0=n2+1:对任意二叉树,若他含有n0个叶子结点,n2个度为2的结点,则必存在的关系式。
特殊的二叉树:
1.满二叉树:高度为h且含有2^h-1个结点的二叉树。
2.完全二叉树:树中共有n个结点,则该n个结点的编号与满二叉树中编号为1至n的结点一一对应。
对于任意一个编号为i的结点
若i=1,为根节点,否则编号为i/2为其双亲节点
若2i>n,该节点无左孩子,否则,编号为2i的节点为左孩子
若2i+1>n,该节点无左孩子,否则,编号为2i+1的节点为右孩子
具有n(n>0)个节点的完全二叉树的高度为:?log2 (n+1)?或者?log2 (n+1) ?
3.偏二叉树:单枝树
存储结构:顺序和链式。
遍历:
1.先序遍历:访问根先序遍历左子树,先序遍历右子树。
void PreOrder(BTNode* b)
{
if (b != NULL)
{
printf("%c", b->data);
PreOrder(b->lchild);
PreOrder(b->rchild);
}
}
2.中序遍历:
void InOrder(BTNode* b)
{
if (b != NULL)
{
InOrder(b->lchild);
printf("%c", b->data);
InOrder(b->rchild);
}
}
3.后序遍历:
void PostOrder(BTNode* b)
{
if (b != NULL)
{
PostOrder(b->lchild);
PostOrder(b->rchild);
printf("%c", b->data);
}
}
哈夫曼树:带权路径长度最小的二叉树。
哈夫曼编码:哈夫曼树中左分支为0,右分支为1.从根节点到叶结点所经过分支对应的0和1组成的序列就是该叶子结点对应字符的编码
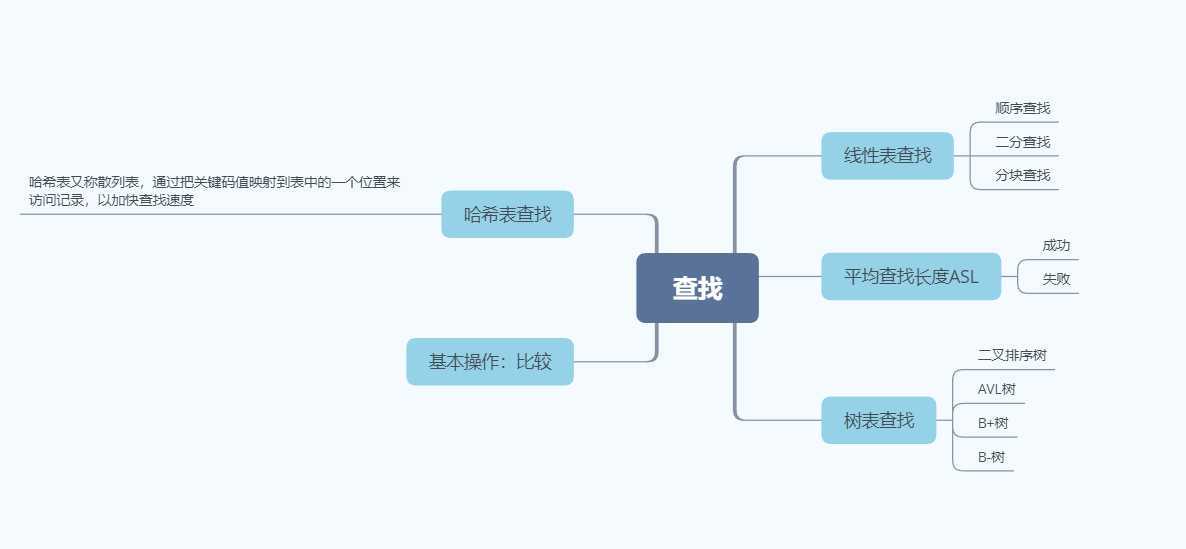
线性表查找:
1.顺序查找:从表的另一端顺序扫描线性表。
2.二分查找:也称折半查找,将关键字与中间位置的节点进行比较
3.分块查找:以二分查找法或顺序查找法查找索引表,以确定待查元素在哪一块,然后在以确定的块中进行顺序查找。
树表查找:
1.二叉排序树:类似二分查找。
2.AVL树
哈希表查找:
基本思路:
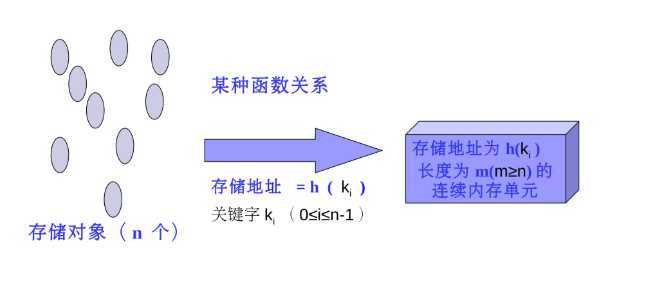
1.直接定址法:h=k+c
2.除留余数法:h(k)=k%p(p最好为素数,p<=k)
3.数字分析法
哈希冲突:
1.线性探测法:d0=h(k)
di=(di-1)mod p(1<=i<=m-1)
2.平方探测法:d0=h(k);
di=(d0+-i^2) mod p;
二叉平衡树的旋转
二叉平衡树在插入或删除一个结点时,先检查该操作是否导致了树的不平衡,若是,则在该路径上查找最小的不平衡树,调节其平衡。
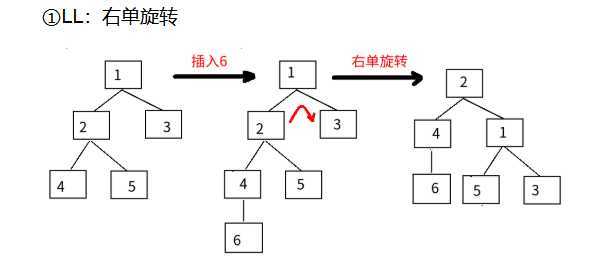
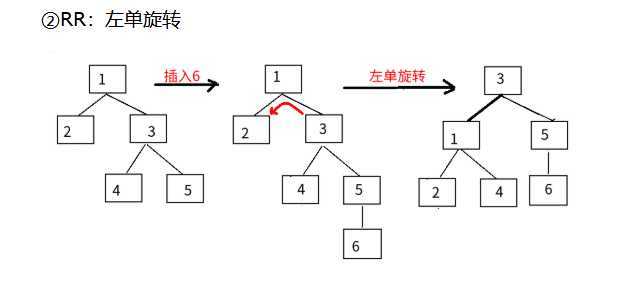
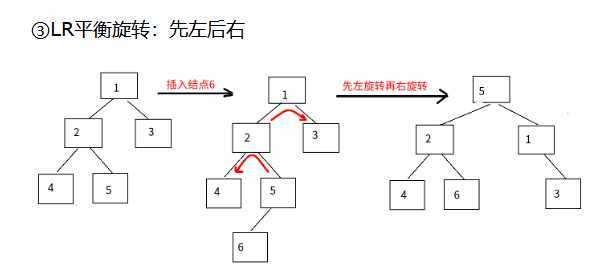
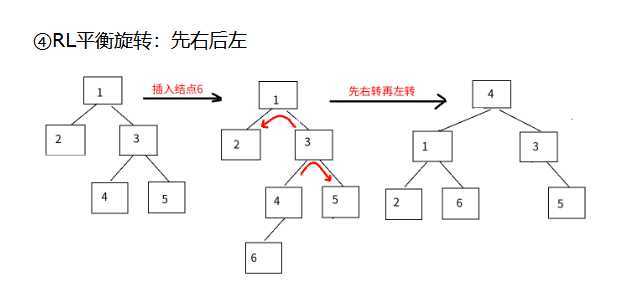
原文:https://www.cnblogs.com/zh18065294222/p/12780717.html