树、二叉树、查找算法总结

一、思维导图

二、重要概念笔记

1、树的基本术语

• 树是n个结点的有限集。
• 树的结点包含一个数据元素及若干个指向其子树的分支。
• 结点拥有的子树数称为结点的度。
• 度为0的结点称为叶子或者终端结点。
• 度不为0的结点称为非终端结点或分支结点。
• 除根结点之外，分支结点也称为内部结点。
• 结点的子树称为该结点的孩子，相应地，该结点称为孩子的双亲。
• 同一个双亲的孩子之间互称兄弟。
• 如果将树中的结点的各子树看成从左到右是有次序的，则称该树为有序树,否则称为无序树。
• 森林是m（m>=0）棵互不相交的树的集合。

2、树的性质

• 树中的结点数等于所有结点的度数之和加一
• 度为m的树中第i层上最多有m的i-1次方个结点(i>=1)
• 高度为h的m次树最多有(m^h-1)/(m-1)个结点
• 具有n个结点的m次树的最小高度为[logm^(n(m-1)+1)]

3、二叉树的性质

• 非空二叉树上的叶子的结点数等于双分支结点数加1
• 非空二叉树的第i层上最多有2^(i-1)个结点.
• 高度为h的二叉树最多有2^h-1个结点
• 具有n个结点的完全二叉树的高度为[log(n+1)]或[logn]+1

4、二叉树的遍历

• 先序遍历————根-左-右
• 中序遍历————左-根-右
• 后序遍历————左-右-根
• 层序遍历————根-逐层从左到右

5、平衡二叉树中插入结点失衡的调整

1、LL型调整

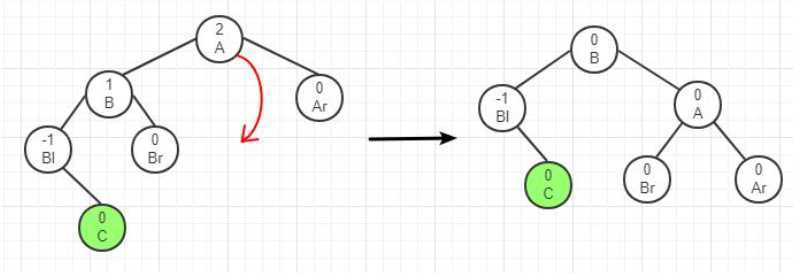
由于在A左子树根结点的左子树上插入结点C，A的平衡因子由1增至2，致使以A为根的子树失去平衡，则需要进行一次向右的顺时针旋转操作，如下图所示。

2、RR型调整

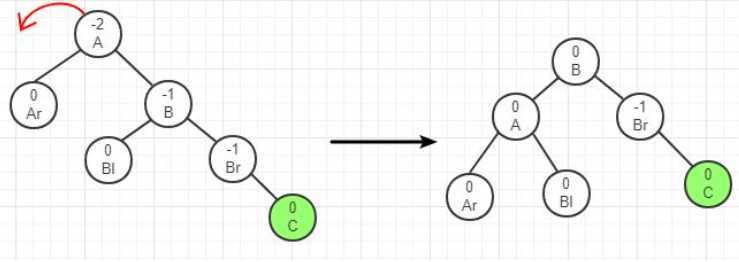
由于在A的右子树根结点的右子树上插入结点C，A的平衡因子由-1变为-2，致使以A为根结点的子树失去平衡，则需进行一次向左的逆时针旋转操作，如下图所示。

3、LR型调整

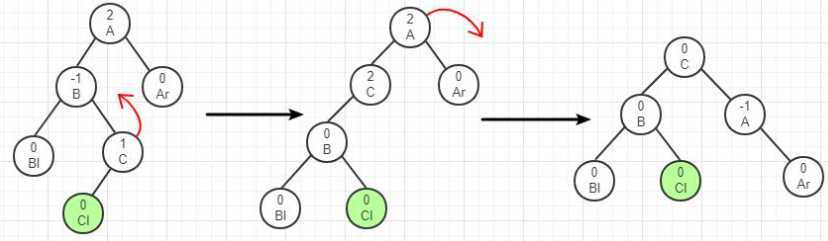
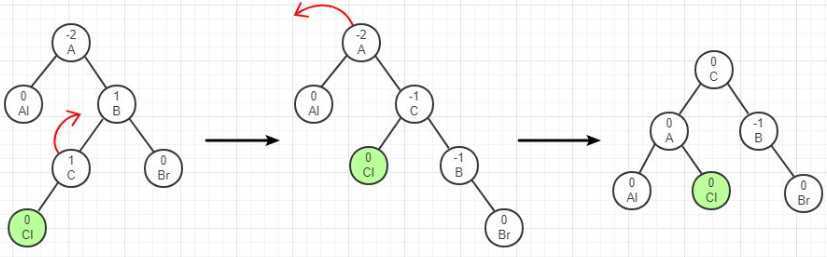
由于在A的左子树根结点的右子树上插入结点，A的平衡因子由1增至2，致使以A为根结点的子树失去平衡，则需要进行二次旋转操作。第一次对B及其右子树进行逆时针旋转，C转上去成为B的根，这时变成了LL型，所以第二次进行LL型的顺时针旋转即可恢复平衡。如果C原来有左子树，则调整C的左子树为B的右子树，如下图所示。

4、RL型调整

由于在A的右子树根结点的左子树上插入结点，A的平衡因子由-1变为-2，致使以A为根结点的子树失去平衡，则旋转方法和LR型相对称，也需进行两次旋转，第一次对B及其左子树进行顺时针右旋，C转上去成为B的根，这时变成了RR型，再进行RR型的逆时针左旋，如下图所示。

6、m阶B_树的特性

• 定义任意非叶子结点最多只有M个儿子，且M>2；
• 根结点的儿子数为[2, M]；
• 除根结点以外的非叶子结点的儿子数为[M/2, M]，向上取整；
• 非叶子结点的关键字个数=儿子数-1；
• 所有叶子结点位于同一层；

7、m阶B+树的特性

• 有n棵子树的非叶子结点中含有n个关键字（b树是n-1个），这些关键字不保存数据，只用来索引，所有数据都保存在叶子节点（b树是每个关键字都保存数据）。
• 所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。
• 所有的非叶子结点可以看成是索引部分，结点中仅含其子树中的最大（或最小）关键字。
• 通常在b+树上有两个头指针，一个指向根结点，一个指向关键字最小的叶子结点。
• 同一个数字会在不同节点中重复出现，根节点的最大元素就是b+树的最大元素。

三、疑难问题及解决方案

• 对二叉排序树的删除操作编写代码时，对于既有左孩子又有右孩子的结点代码逻辑理解很模糊不清，无法实现函数代码编写
• 解决方案：

void DeleteBST(TreeNodeP &T, int key)
{
	if (T == NULL)
	{
		return;
	}
	else
	{
		if (key > T->data)
		{
			DeleteBST(T->rchild, key);
		}
		else if (key < T->data)
		{
			DeleteBST(T->lchild, key);
		}
		else
		{
			Delete(T);
			return;
		}
	}
}
void Delete(TreeNodeP &T)
{
	TreeNodeP q = T;
	if (T->lchild == NULL)
	{
		q = T;
		T = T->rchild;
		free(q);
	}
	else if (T->rchild == NULL)
	{
		q = T;
		T = T->lchild;
		free(q);
	}
	else
	{
		Deletel(T, T->lchild);
	}
}
void Deletel(TreeNodeP& T, TreeNodeP& p)
{
	TreeNodeP q;
	if (p->rchild != NULL)
	{
		Deletel(T, p->rchild);
	}
	else
	{
		T->data = p->data;
		q = p;
		p = p->lchild;
		free(q);
	}
}

树、二叉树、查找算法总结

原文：https://www.cnblogs.com/zx224569/p/12781418.html