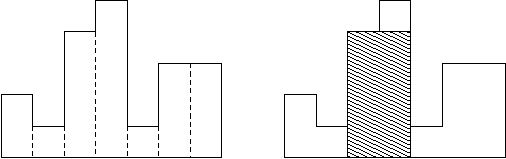
如上图所示,我们看这代码分析
首先,单调栈必须保证单调对吧,所以说我们将大于栈顶元素的元素入栈,直到遇到一个小于栈顶元素的数,然后因为是单调栈,所以我们想让它入栈,就必须删除栈中比他大的元素,但是又要不影响结果,所以每个栈顶元素出栈是都要计算它与前面出栈元素组成的最大矩形,直到在栈中找到一个比待入栈元素小的数。然后插入到它的旁边。
有的人可能会问,这怎么不会使结果变化呢?,因为我们,出栈时已经计算了前面最大的值出来,所以后面的数在入栈时同样结果不变。
推荐手动模拟一下,下图没模拟完
1 #include <iostream> 2 #include <algorithm> 3 using namespace std; 4 const int N = 1e5 + 5; 5 6 using ll = long long; 7 8 ll a[N], s[N], w[N]; 9 10 ll ans; 11 int n, p; 12 int main() { 13 while(cin >> n, n) { 14 ans = 0, p = 0; 15 16 for(int i = 1; i <= n; ++ i) cin >> a[i]; 17 a[n+1] = 0; 18 for (int i = 1; i <= n + 1; ++ i) { 19 if (a[i] > s[p]) s[++p] = a[i] , w[p] = 1;//单调入栈 20 else { 21 int width = 0; 22 while(s[p] > a[i]) {//将栈顶元素和要入栈的元素相比,大的出栈; 23 width += w[p];//加上宽度 24 ans = max(ans, (ll)width * s[p]);//每次计算面积最大值 25 p--;//出栈 26 } 27 s[++p] = a[i], w[p] = width + 1;//将其入栈,这是不边的关键代码 28 29 } 30 } 31 cout << ans << endl; 32 } 33 }
原文:https://www.cnblogs.com/rstz/p/12781719.html