组合数相关

组合数

1.定义：从n个不同元素中，任取m(m≤n)个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；从n个不同元素中取出m(m≤n)个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。

2.公式：在线性写法中被写作C(n,m)。

        组合数的计算公式为（由排列数公式得到）

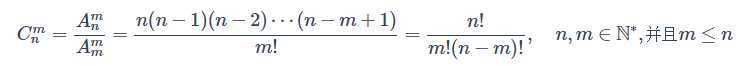
3.公式拓展：

(1)组合数的递推公式，组合数可以写为C(n,m)=C(n-1,m-1)+C(n-1,m)，可用于递归求组合数的值。

   证明：思路一：可以用组合数公式证明。

         思路二(更重要)：从n个元素中任意指定一个元素。则选出m个的方法中，包含这一个元素的有C（n-1，m-1）种组合，不包含这一个元素的有C（n-1，m）种组合。

(2)二项式定理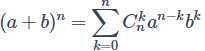，其中展开式的第r+1项为。

(3)组合数的求和公式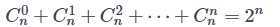，，一般在二项式定理中或者多项式的展开式中应用。

(4)和(3)类似的公式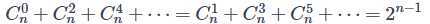：(由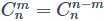推导而来)。

(5)互补性质，从n个不同元素中取出m个元素的组合数=从n个不同元素中取出 (n-m) 个元素的组合数。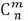

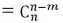   理解：例如C(9,2)=C(9,7)，即从9个元素里选择2个元素的方法与从9个元素里选择7个元素的方法是相等的。

   规定：C(n,0)=1  C(n,n)=1  C(0,0)=1

(6)组合恒等式，C(n,m)=C(n,n-m)=C(n-1,m-1)+C(n-1,m)（其实和公式(1)一样，只不过可以表示不同的意义）。

   这个公式可以表示在 n 个物品中选取 m 个物品。

(7)可重复组合数(上面为不可重复组合数)，其定义为从个不同的元素中，每次取出个可以重复的元素并成一组，叫做从个不同的元素每次取出个元素的允许重复的组合，即重复组合，其组合总数记作。

公式为。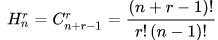

(8)不相邻组合数，是指从集合A={1,2,...,n}中取出r个不相邻的数字进行组合（不可重），即不存在相邻的两个数j,j+1的组合，其组合数为C(n-r+1,r)。

4.求组合数的相关算法：

主函数如下：

1 int main()
2 {
3     int n,m;
4     int ans;
5     cin>>n>>m;
6     ans=cal(n,m);
7     cout<<ans;
8     return 0;    
9 } 

(1)即利用3中的(1)递归公式。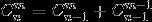

递归方法：

int cal(int n,int m)//递归计算组合数 
{
    if(n==m||m==0)
    return 1;
    return  cal(n-1,m-1)+cal(n-1,m);
}

 非递归方法（杨辉三角打表）：

 1 int val[50][50];
 2 int cal(int n,int m)
 3 { 
 4     for(int i=0;i<n+1;i++)
 5     {
 6         for(int j=0;j<=i;j++)
 7         {
 8         if(i==j||j==0)
 9         val[i][j]=1;
10         else val[i][j]=val[i-1][j]+val[i-1][j-1];
11         }
12     }
13     return val[n][m];
14 }

(2)公式打表(利用公式)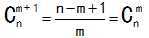

代码如下：

1 int val[60];
2 int cal(int n,int m)//val[i]即为val(n,i)的值
3 {
4     val[0]=1;
5     for(int i=1;i<=n;i++)
6         val[i]=val[i-1]*(n-i+1)/i;
7     return val[m];
8 }

组合数相关

原文：https://www.cnblogs.com/theshorekind/p/12775276.html