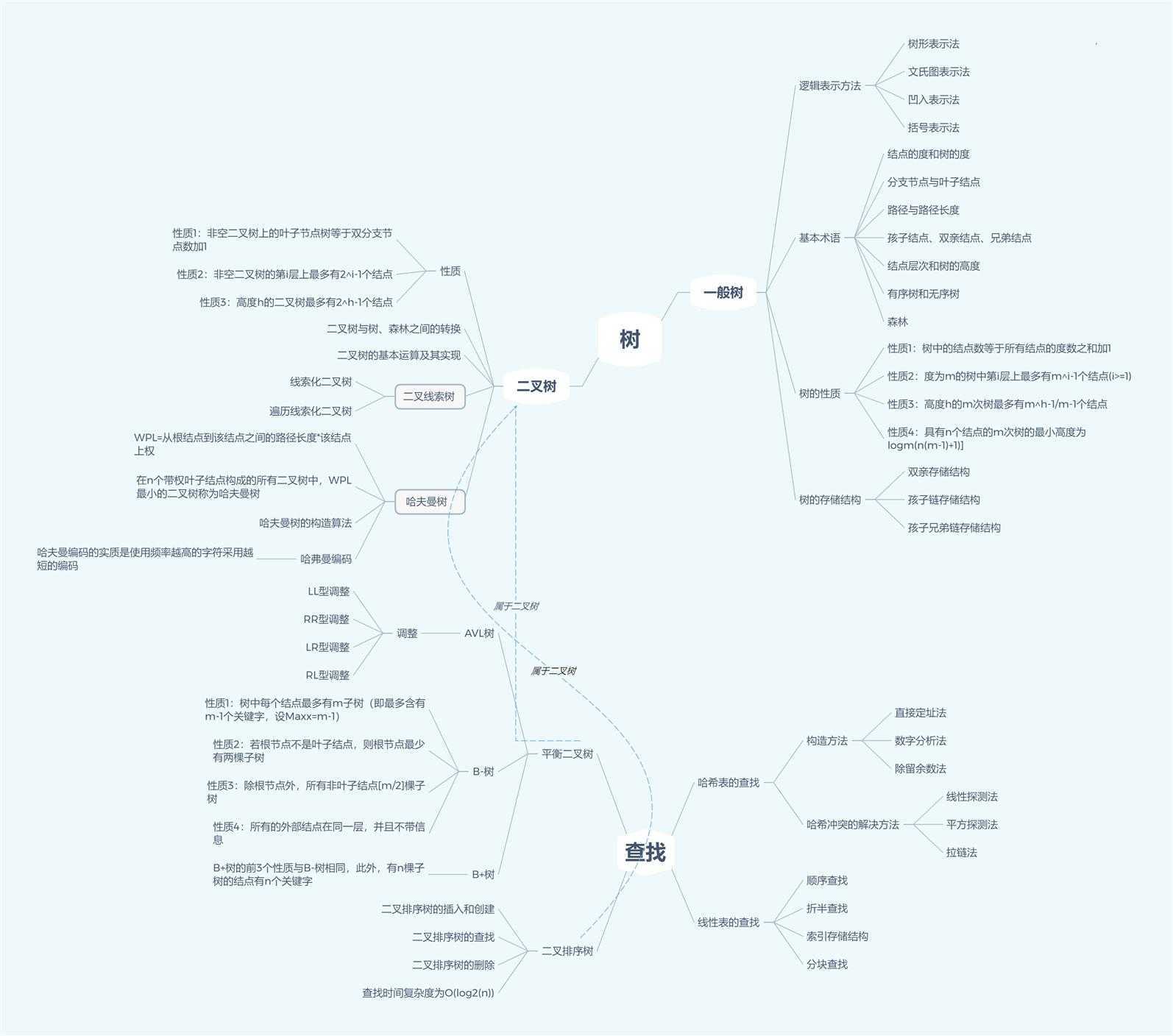
性质1:树中的结点数等于所有结点的度数之和加1
性质2:度为m的树中第i层上最多有m^i-1个结点(i>=1)
性质3:高度h的m次树最多有m^h-1/m-1个结点
性质4:具有n个结点的m次树的最小高度为logm(n(m-1)+1)]
先根遍历:若树不空,则先访问根节点,然后依次先根遍历各棵子树
后根遍历:若树不空,则先依次后根遍历各棵子树,然后访问根节点
例子:

先序遍历、中序遍历、后序遍历
先序遍历:若森林不空,则访问森林中第一棵树的结点;先序遍历森林中第一棵树的子树森林;先序遍历森林中(除第一棵树外)其余树构成的森林。
中序遍历:若森林不空,中序遍历森林中第一棵树的子树森林;访问森林中第一棵树的根节点;中序遍历森林中(除第一棵树外)其余树构成的森林。即:依次从左至右对森林的每一棵树进行后根遍历。

任何n个不同结点的二叉树,都可由它的中序序列和先序序列唯一地确定。
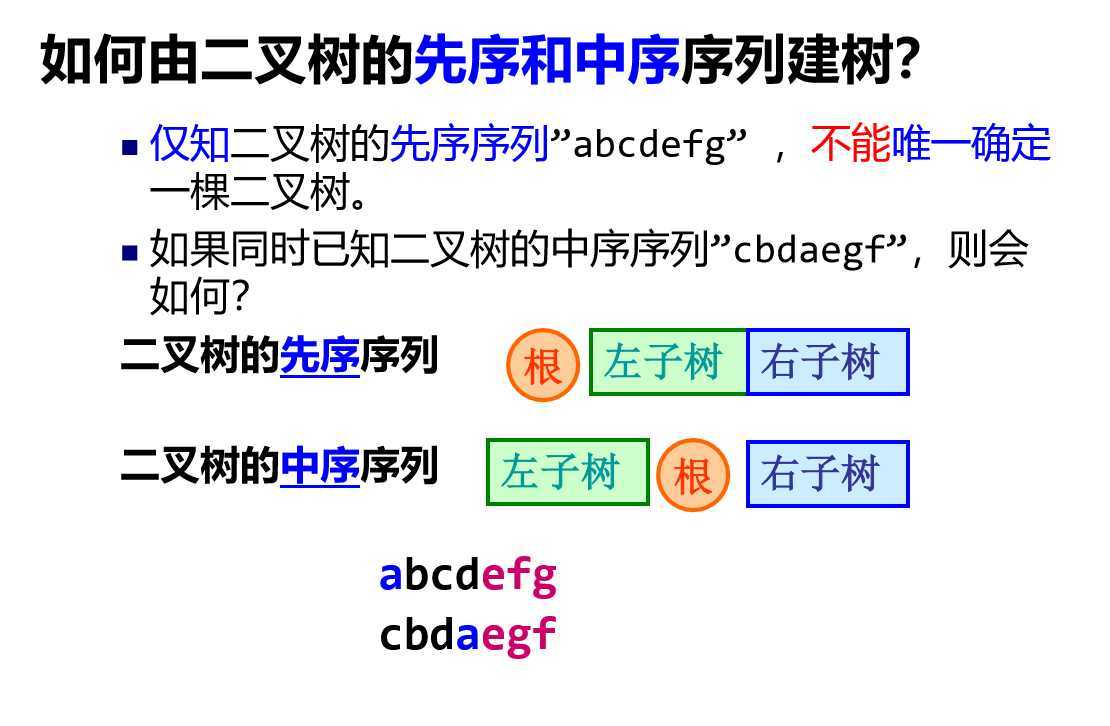
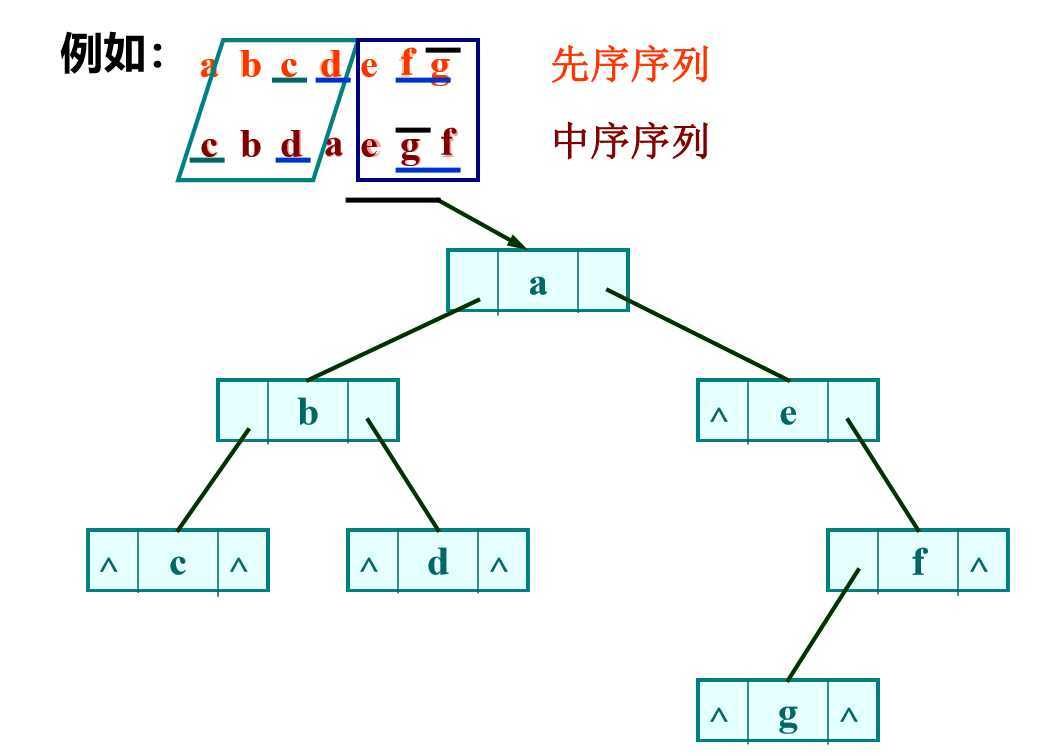
任何n个不同结点的二叉树都可由它的中序序列和后序序列唯一地确定。

如图:

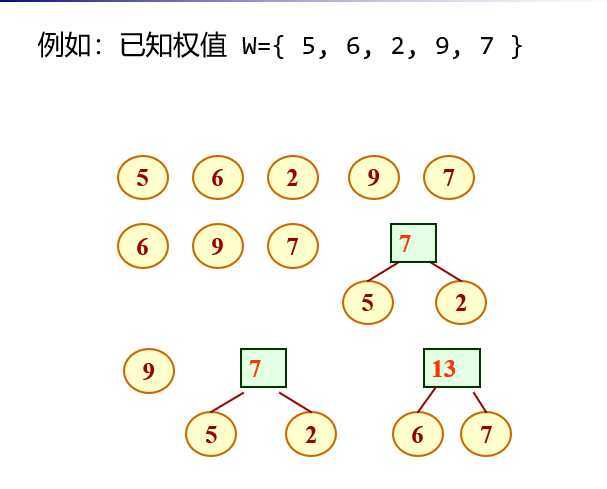
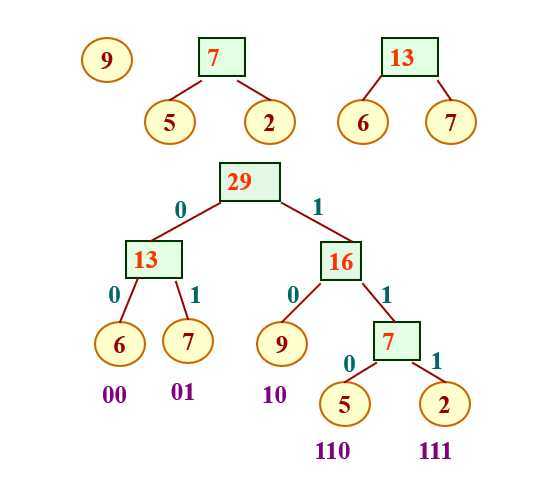
二叉排序树查找的性能分析:

为了尽量提高二叉排序树的查找效率,引入平衡二叉树。
AVL树查找的性能分析:


B-树的分裂:插入时若插入的结点关键字数量=Max,则需要分裂
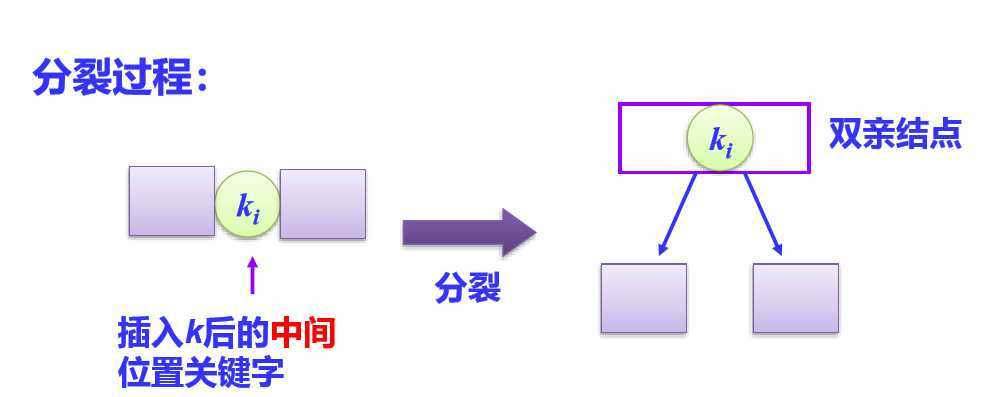
B-树的合并:删除时若删除的叶子结点关键字数量=Min,则需要合并
包括插入、创建、删除等
#include<iostream>
using namespace std;
typedef int KeyTyped;
typedef struct Node {
int key;
struct Node* lchild;
struct Node* rchild;
}BSTNode;
BSTNode* SearchBST(BSTNode* T, int k);
bool InsertBST(BSTNode*& bt, int k);
BSTNode* CreateBST(int a[], int n);
void InOrder(BSTNode* bt);
bool DeleteBST(BSTNode*& bt, int k);
void Delete(BSTNode* p, BSTNode*& r);
int main(){
int i, n, a[100], k;
printf("请输入二叉排序树的结点个数:");
cin >> n;
printf("请输入二叉排序树结点值:\n");
for (i = 0; i < n; i++) {
cin >> a[i];
}
BSTNode* root = CreateBST(a, n);
printf("请输入要删除的结点:");
cin>>k;
printf("该二叉树删除前中序遍历序列为:\n");
InOrder(root);
printf("\n该二叉树删除后中序遍历序列为:\n");
DeleteBST(root, k);
InOrder(root);
return 0;
}
BSTNode* SearchBST(BSTNode* T, int k) {
if (T == NULL || T->key == k) {
return T;
}
if (k < T->key) {
return SearchBST(T->lchild, k);
}
else {
return SearchBST(T->rchild, k);
}
}
bool InsertBST(BSTNode*& bt, int k) {
if (bt == NULL) {
bt = new BSTNode;
bt->key = k;
bt->lchild = bt->rchild = NULL;
return true;
}
else if (k == bt->key) {
return false;
}
else if (k < bt->key) {
return InsertBST(bt->lchild, k);
}
else {
return InsertBST(bt->rchild, k);
}
}
BSTNode* CreateBST(int a[], int n) {
BSTNode* bt = NULL;
int i = 0;
while (i < n) {
InsertBST(bt, a[i]);
i++;
}
return bt;
}
void InOrder(BSTNode* bt) {
if (bt != NULL) {
InOrder(bt->lchild);
printf("%d ", bt->key);
InOrder(bt->rchild);
}
}
bool DeleteBST(BSTNode*& bt, int k) {
if (bt == NULL) {
return false;
}
else {
if (k < bt->key) {
return DeleteBST(bt->lchild, k);
}
else if (k > bt->key) {
return DeleteBST(bt->rchild, k);
}
else {
BSTNode* q;
if (bt->lchild == NULL) {
q = bt;
bt = bt->rchild;
free(q);
}
else if (bt->rchild == NULL) {
q = bt;
bt = bt->lchild;
free(q);
}
else {
Delete(bt, bt->lchild);
}
}
}
}
void Delete(BSTNode* p, BSTNode* &r) {
BSTNode* q;
if (r->rchild != NULL) {
Delete(p, r->rchild);
}
else {
p->key = r->key;
q = r;
r = r->lchild;
free(q);
}
}
void InOrderl(BTNode* b) {
BTNode* p;
SqStack* st;
InitStack(st);
p = b;
while (!StackEmpty(st) || p != NULL) {
while (p != NULL) {
Push(st, b);
p = p->lchild;
}
if (!StackEmpty(st)) {
pop(st, p);
printf("%c", p->data);
p = p->rchild;
}
}
printf("\n");
DestroyStack(st);
}
jmu-ds-表达式树
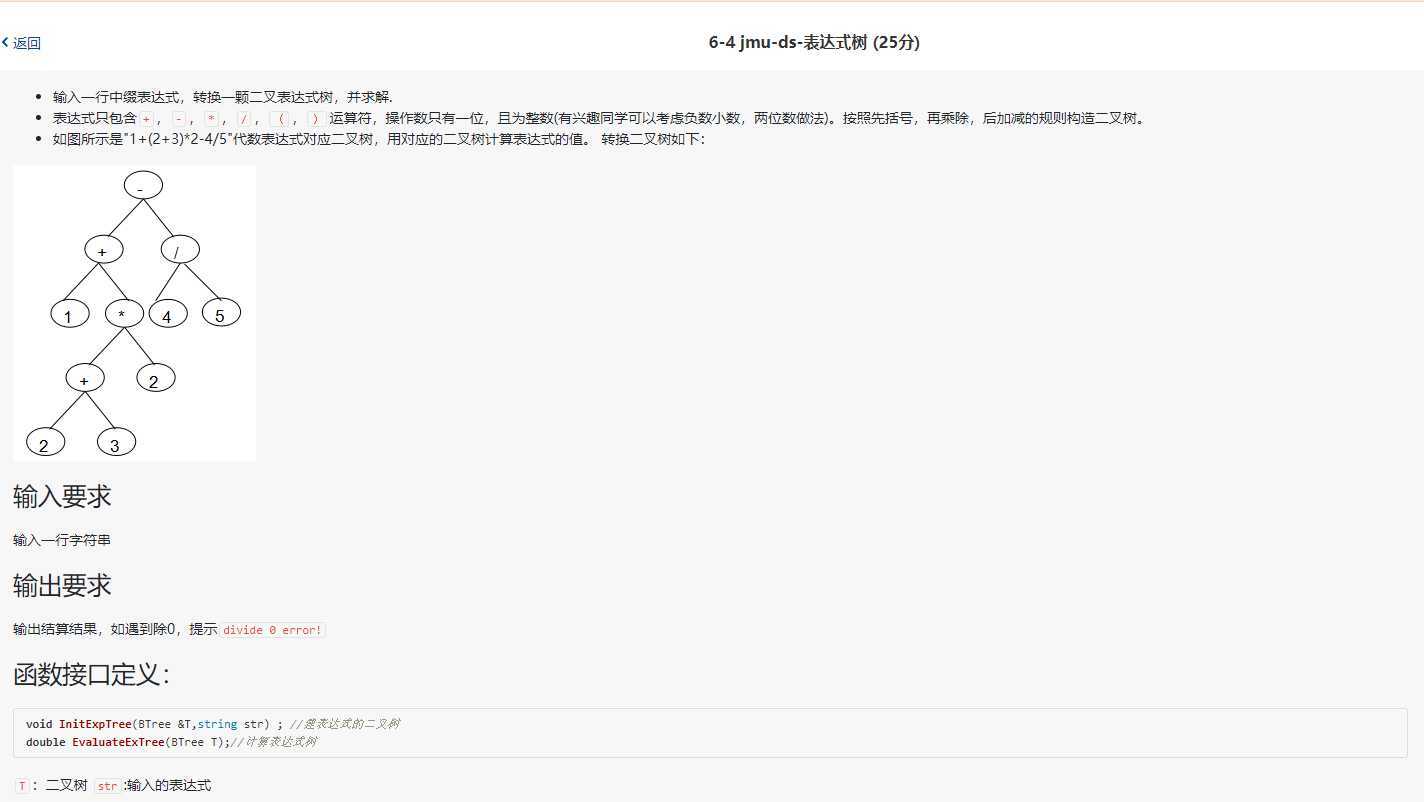
裁判测试程序样例:
#include<iostream>
#include<string>
#include<stack>
using namespace std;
typedef struct BiTNode{ //二叉树的二叉链表存储表示
char data;
struct BiTNode *lchild,*rchild;
}BTNode,*BTree;
void InitExpTree(BTree &T,string str) ; //建二叉表达式树
double EvaluateExTree(BTree T);//计算表达式树
char Precede(char t1,char t2) ;//比较t1,t2运算符优先级函数
int In(char c) ;//判断c是否运算符
void CreateExpTree(BTree &T,BTree a,BTree b,char ch);//建简单二叉树
void DestroyBTree(BTree bt);//销毁树
int main()
{
string str;
BTree T;
getline(cin,str);
InitExpTree(T,str); //创建表达式树
cout<<EvaluateExTree(T); //输出值
DestroyBTree(T);
return 0;
}
char Precede(char t1,char t2)
{ /*判断两符号的优先关系 */
char f;
switch(t2)
{
case ‘+‘: if(t1==‘(‘||t1==‘#‘) f=‘<‘;
else f=‘>‘;
break;
case ‘-‘: if(t1==‘(‘||t1==‘#‘) f=‘<‘;
else f=‘>‘;
break;
case ‘*‘:if(t1==‘*‘||t1==‘/‘||t1==‘)‘) f=‘>‘;
else f=‘<‘;
break;
case ‘/‘:if(t1==‘*‘||t1==‘/‘||t1==‘)‘) f=‘>‘;
else f=‘<‘;
break;
case ‘(‘: if(t1!=‘)‘) f=‘<‘;
break;
case‘)‘: if(t1==‘(‘) f=‘=‘;
else f=‘>‘;
break;
case‘#‘: if(t1==‘#‘) f=‘=‘;
else f=‘>‘;
}
return f;
}
int In(char c)
{ /* 判断c是否为运算符 */
switch(c)
{
case ‘+‘:
case‘-‘:
case‘*‘:
case ‘/‘:
case‘#‘:
case ‘(‘:
case‘)‘:return 1;break;
default:return 0;
}
}
void CreateExpTree(BTree &T,BTree a,BTree b,char ch)
{ //简单二叉树的创建
T=new BTNode;
T->data=ch;
T->lchild=a;
T->rchild=b;
}
void DestroyBTree(BTree bt)//销毁树
{
if(bt!=NULL)
{
DestroyBTree(bt->lchild);
DestroyBTree(bt->rchild);
delete bt;
}
}
/* 请在这里填写答案 */
解决方案:
void InitExpTree(BTree& T, string str){
stack<BTree>node;
stack<char>op;
int i = 0;
BTree p, a, b;
while (str[i]) {
if (!In(str[i])) {
p = new BTNode;
p->data = str[i];
p->lchild = p->rchild = NULL;
node.push(p);
}
else {
if (op.empty()) {
op.push(str[i]);
}
else {
switch (Precede(op.top(), str[i])) {
case ‘<‘:
op.push(str[i]);
break;
case ‘=‘:
op.pop();
break;
case ‘>‘:
a = node.top();
node.pop();
b = node.top();
node.pop();
CreateExpTree(p, b, a, op.top());
op.pop();
node.push(p);
i--;
break;
}
}
}
i++;
}
while (!node.empty() && !op.empty()) {
a = node.top();
node.pop();
b = node.top();
node.pop();
CreateExpTree(p, b, a, op.top());
op.pop();
node.push(p);
}
T = p;
}
double EvaluateExTree(BTree T) {
double num1, num2;
double result = 0;
if (!T) return 0;
if (T != NULL && !T->lchild && !T->rchild) {
return T->data - ‘0‘;
}
num1 = EvaluateExTree(T->lchild);
num2 = EvaluateExTree(T->rchild);
switch (T->data) {
case ‘+‘:result += num1 + num2; break;
case ‘-‘:result += num1 - num2; break;
case ‘*‘:result += num1 * num2; break;
case‘/‘:
if (num2 == 0) {
cout << "divide 0 error!";
exit(0);
}
result += num1 / num2;
break;
}
return result;
}
(1)倒排索引和稠密索引的原理和实现形式不是很清楚
(2)B-树和B+树的创建、查找、删除、插入等运算的代码实现
(3)平衡二叉树调整时的 平衡旋转 还是看不明白
原文:https://www.cnblogs.com/cjt0722/p/12780497.html