一.思维导图

重要概念的笔记

树与二叉树

1.满二叉树：指的是深度为k且含有2k-1个结点的二叉树

  特点：是每一层上的结点数都是 最大结点数

2.完全二叉树：树中所含的 n 个结点和满二叉树中 编号为 1 至 n 的结点一一对应

  特点：⑴叶子结点只可能在层次最大 的两层出现
        ⑵对任一结点，若其右 分支下的子孙的最大层次为l，则其左 分支下的子孙的最大层次为l或l+1

3.中序遍历的递归算法(先序和后序类似)

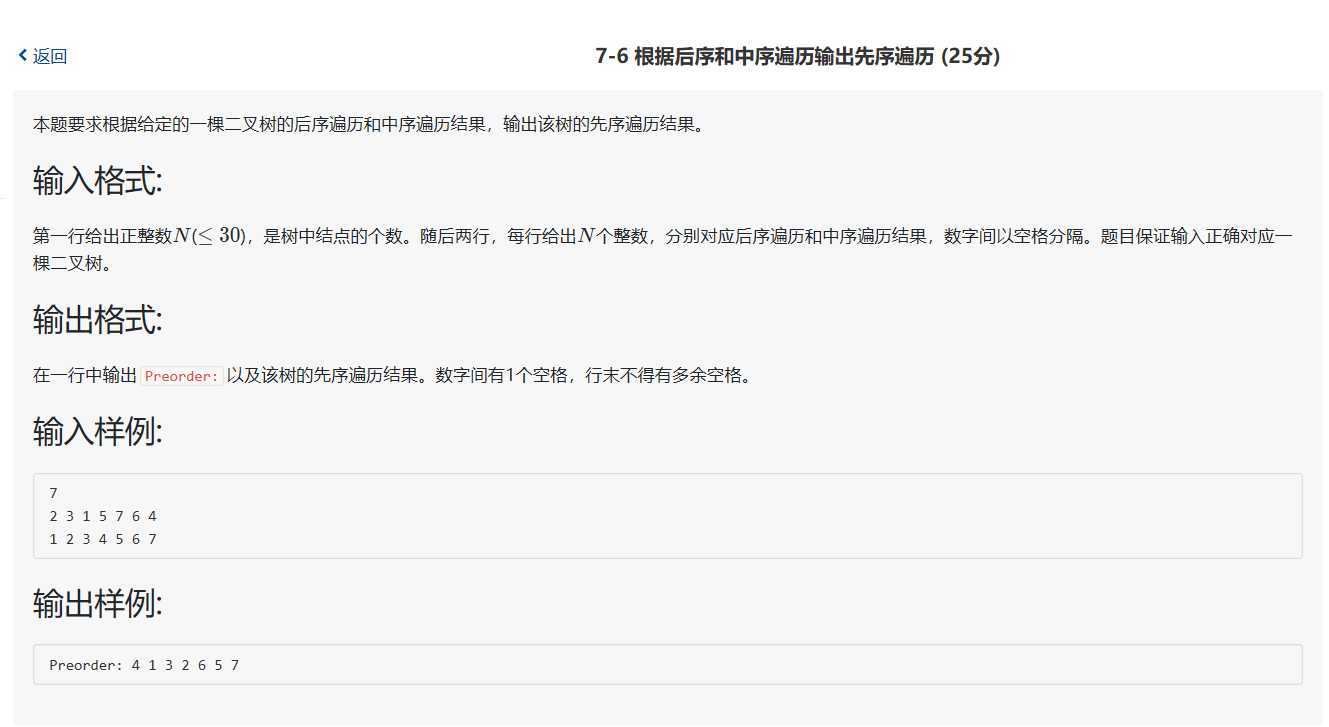
void preorder(BiTree T)
{
  if(T){
    preorder(T->lchild);
    cout<<T->data;
    preorder(T->rchild);
 }
}

4.中序遍历的非递归算法

void InOrderTraverse(BiTree T)
{ 
 InitStack(S); p = T; 
 while (p || !StackEmpty(S)){ 
      if (p){ 
         Push(S, p); p = p->lchild; 
      }
      else{ 
         Pop(S, q); 
         cout << q->data; 
         p = q->rchild; 
          } 
  } 
} 

哈夫曼树

1.叶子节点为n的哈夫曼树共有2n-1个节点
2.哈夫曼树不唯一，但可以找查找长度最短的哈夫曼树

查找

1.查找表：由同一类型的数据元素(或记录)构成的集合

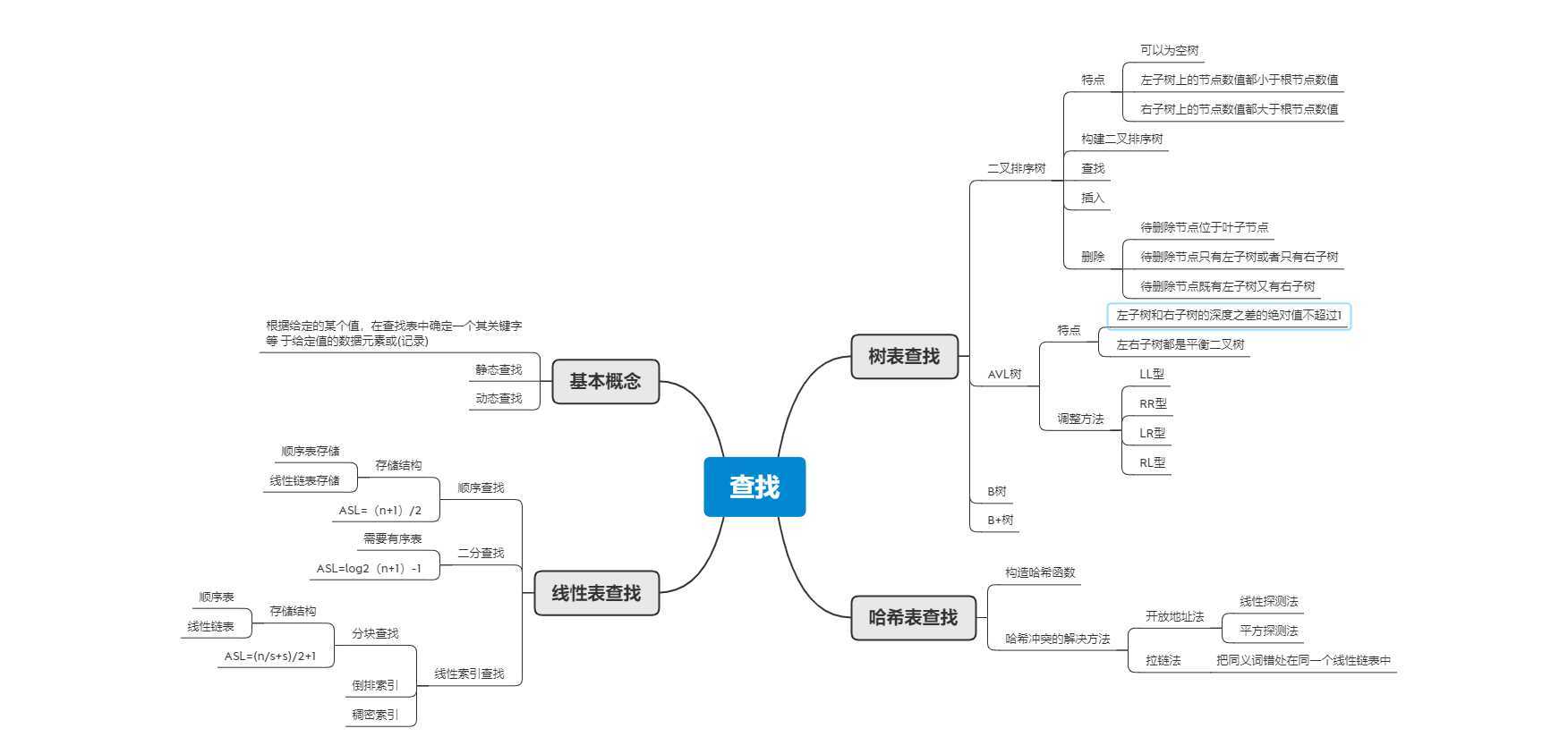
  类别：静态查找和动态查找
  ①静态查找：仅作查询和检索操作的查找表
  ②动态查找：有时在查询之后，还需要将“查询”结果为“不在 查找表中”的数据元素插入到查找表中 或者，从查找表中删除其“查询”结果为“在查找 表中”的数据元素

2.二叉排序树

  ①可以为空树
  ②含有n个结点的二叉排序树的平均查找长度和树的形态有关
  ③平均查找长度和二叉树的形态有关。
    最好：log2n（形态匀称，与二分查找的判定树相似）
    最坏: （n+1)/2（单支树）

3.B树与B+树

B树
①m阶B树的非根节点的孩子个数最多有m个，最少有m/2（向上取整）个
②关键字个数最多有m-1个，最少有m/2-1个

B+树
①m阶B+树的每个分支节点至多有m棵子树
②有n棵子树的节点有n个关键字
③叶子节点包含全部关键字及指向相应记录的指针

4.哈希查找

  ①哈希表：将一组关键字映像到一个有限的、地址连续的地址 集 (区间) 上，并以关键字在地址集中的“像”作为 相应记录在表中的存储位置，如此构造所得的查找表 称之为“哈希表“
  ②处理冲突的方法：开放定址，链地址法
    链地址法：将所有哈希地址相同的记录都链接在同一链表中
  ③决定哈希表查找的ASL的因素：
    选用的哈希函数
    选用的处理冲突的方法
    哈希表饱和的程度，装载因子（a=n/m）值的大小(n：记录数，m：表的长度)

疑难问题及解决方案

对B树与B+树的操作不太理解

通过看课件以及百度查找了解到了

B树的插入操作：

  ①插入后，该结点的关键字个数n<m，不修改指针;
  ②插入后，该结点的关键字个数 n=m，则需进行 “结点分裂”，令 s = ?m/2?，在原结点中保留 (A0，K1，……  ， Ks-1，As-1)；建新结点(As， Ks+1，……  ，Kn，An)；将(Ks, p)插入双亲节点             
  ③若双亲为空，则建新的根结点

B+树的查找：

  ①直接从最小关键字开始进行顺序查找所有叶节 点链接成的线性链表 
  ②从B+树的根节点出发一直找到叶节点为止

Pta（还不是很懂）

树，二叉树，查找算法总结

原文：https://www.cnblogs.com/cxdscx/p/12780744.html