1.树

1.树的定义：

树是n(n>=0)个节点的有限集合T，是一个递归定义。

2.树的基本术语：

1.节点的度：节点拥有的子树数量
2.树的度：树中所有节点的度的最大值
3.叶子：度为0的节点
4.树的深度：树中叶子节点所在的最大层次
5.森林：n棵不相交树的集合

树的遍历：

先根遍历，后根遍历，没有中根遍历，这点和二叉树不同。

思维导图如下：

2.二叉树

二叉树的性质

1.在二叉树的第i层上至多有2^(i-1)个结点（i>0）。
2.深度为k的二叉树至多有2^k-1个结点（k>0）。
3.对于任意一棵二叉树，如果其叶结点为N0，而度数为2的结点总数为N2，则N0=N2+1。
4.具有n个结点的完全二叉树的深度必为 log2(n）+1。
5.对完全二叉树，若从上至下、从左只右编号，则编号为i的节点，其左孩子编号必为2i，其有孩子编号必为2i+1；其双亲的编号必为i/2（i=1时为根 除外）。
6.二叉树的节点数的分支树加1.

二叉树的存储结构

顺序存储，链式存储

二叉树的遍历

先序遍历：根左右
中序遍历：左根右
后序遍历：左右根

二叉排序树

从根节点开始插入，大于根节点的往右，小于根节点的往左，这样最多查找次数就等于树的高度。

线索二叉树

在原有的二叉排序树上加入线索，更快的找到前驱和后继。

AVL树

树中每个节点的左右子树深度之差，绝对值不大于1.它是二叉排序树的升级版，它的高度更低，查找速度更快。

B-树(这是一种多路查找法)

基本性质：
1.定义任意非叶子结点最多只有M个儿子，且M>2
2.根结点的儿子数为[2, M]
3.除根结点以外的非叶子结点的儿子数为[M/2, M]，向上取整
4.非叶子结点的关键字个数=儿子数-1
5.所有叶子结点位于同一层

B+树（相对于B-树来说，它还能顺序查找）

基本性质：
1.有n棵子树的非叶子结点中含有n个关键字（B树是n-1个），这些关键字不保存数据，只用来索引，所有数据都保存在叶子节点（B树是每个关键字都保存数据）。
2.所有的叶子结点中包含了全部关键字的信息，及指向含这些关键字记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。

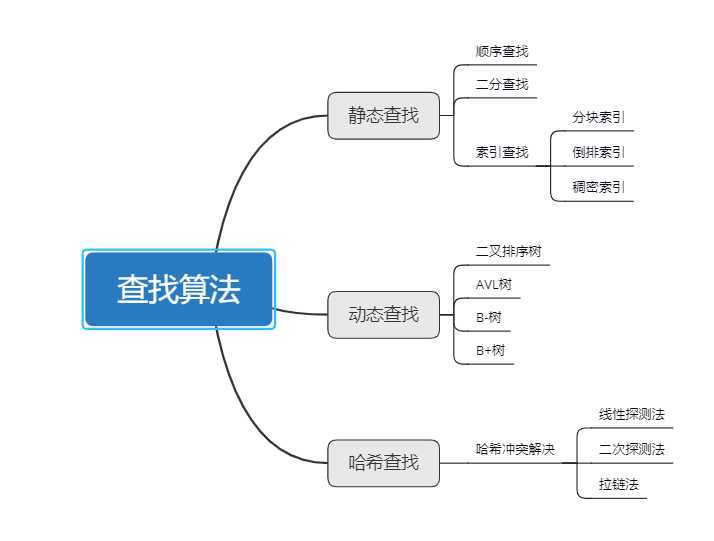
思维导图如下：

3.查找算法总结

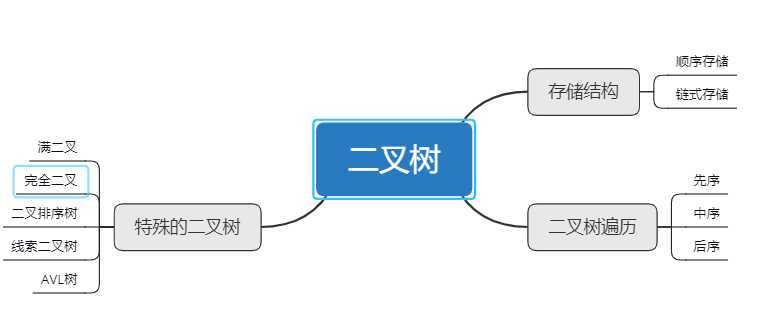
思维导图如下：

4.疑难问题及解决方案：

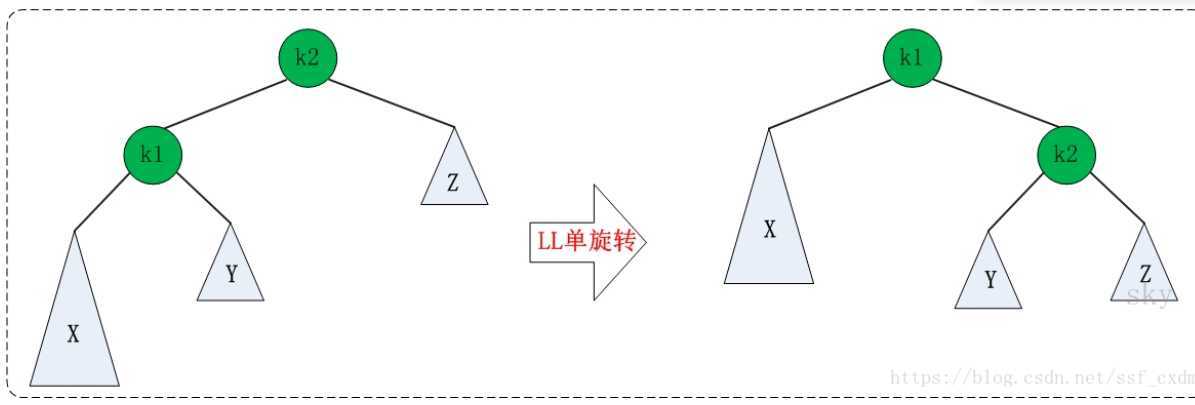
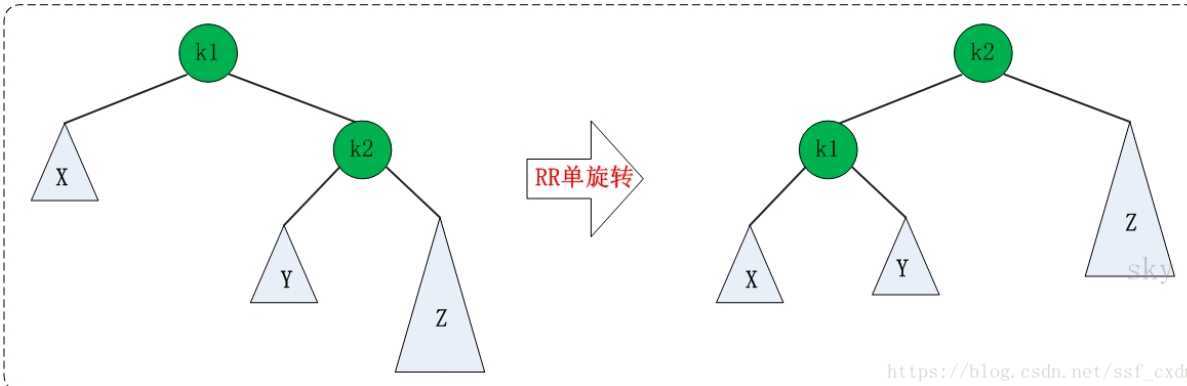
对平衡二叉树构建的四种调整方法的总结，包括LL型，RR型，LR型，RL型。

LL型调整

RR型调整

LR型调整

RL型调整

对于后面两种形态的调整，就是先把LR转化成LL，然后进行LL调整。把RL转化成RR，然后进行RR调整。

5.总结

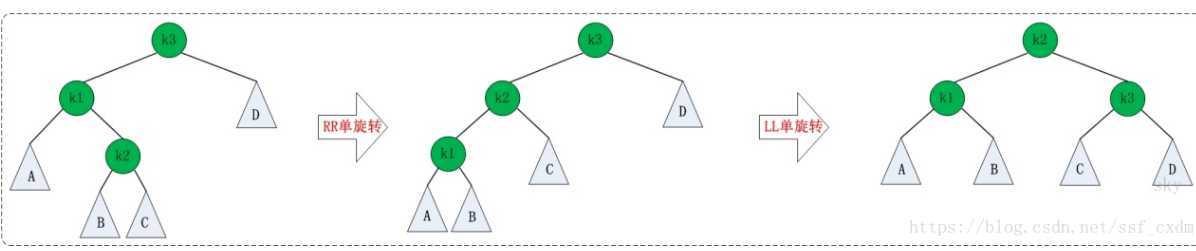
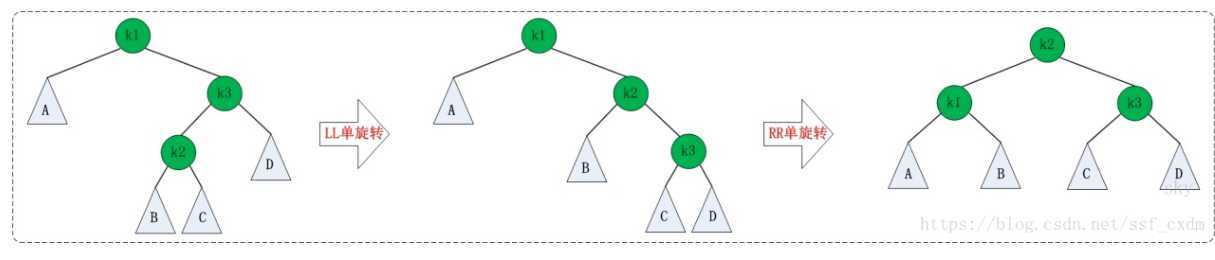
1.对于B-树和B+树的一些题目，还不够熟悉，主要在节点分裂、合并这块。
2.平时PTA的习题量做得不够，导致对一些知识点掌握不够熟练。

树、二叉树、查找算法总结

原文：https://www.cnblogs.com/yj-123/p/12782062.html