给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
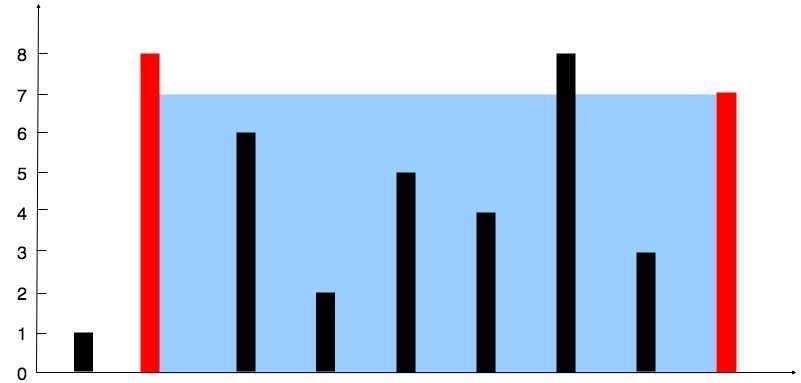
示例:
输入:[1,8,6,2,5,4,8,3,7]
输出:49
思路:使用双指针,开始指向左右边界。每次将对应的数字较小的那个指针往另一个指针的方向移动一个位置,表示我们认为这个指针不可能再作为容器的边界了。并检查是否要更新面积最大值,直到两个指针指向同一个位置。
为什么每次都移动对应数字小的那一个指针?
假设当前左指针和右指针指向的数分别为 x和 y,不失一般性,我们假设x≤y。同时,两个指针之间的距离为 t。那么,它们组成的容器的容量为:
min(x, y) * t = x * t
我们可以断定,如果我们保持左指针的位置不变,那么无论右指针往左怎么移动,这个容器的容量都不会超过 x * t了。
1 class Solution { 2 public: 3 int maxArea(vector<int>& height) { 4 int l = 0, r = height.size() - 1; 5 int ans = 0; 6 while (l < r) { 7 int area = min(height[l], height[r]) * (r - l); 8 ans = max(ans, area); 9 if (height[l] <= height[r]) { 10 ++l; 11 } 12 else { 13 --r; 14 } 15 } 16 return ans; 17 } 18 };
这是第一次遇到这个问题时的自己的做法,记录一下
1 class Solution { 2 public: 3 int maxArea(vector<int>& height) { 4 int n=height.size(); 5 if(n<2) return 0; 6 int left(0),right(n-1),maxarea(0);int minh; 7 int leftTaller=0; 8 int rightTaller=0; 9 for(;left<n;left++) 10 { 11 if(height[left]>leftTaller)//如果不大于,不用进行计算比较更新maxarea,因为根本不肯大于maxarea 12 { 13 leftTaller=height[left]; 14 minh=height[left]<height[right]?height[left]:height[right]; 15 maxarea=maxarea>(minh*(right-left))?maxarea:(minh*(right-left)); 16 right--; 17 while(right>left) 18 { 19 if(height[right]>rightTaller)//只有大于才要检查是否要更新maxarea 20 { 21 rightTaller=height[right]; 22 minh=height[left]<height[right]?height[left]:height[right]; 23 maxarea=maxarea>(minh*(right-left))?maxarea:(minh*(right-left)); 24 } 25 right--; 26 } 27 right=n-1; 28 rightTaller=height[right]; 29 } 30 } 31 return maxarea; 32 } 33 };

原文:https://www.cnblogs.com/cs0915/p/12781844.html