一、思维导图

二、相关概念

树

概念：它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
相关术语
结点的度：一个结点含有的子结点的个数称为该结点的度；
叶结点：度为0的结点称为叶结点；
父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点；
孩子结点：一个结点含有的子树的根结点称为该结点的子结点；
兄弟结点：具有相同父结点的结点互称为兄弟结点；
树的度：一棵树中，最大的结点的度称为树的度；
树的高度：树中结点的最大层次；。
森林：由m（m>=0）棵互不相交的树的集合称为森林；

表示方法

图像表达法
符号表达法
遍历表达法：先序遍历、中序遍历、后序遍历

基本操作

构造树
判断树是否为空
获取树的深度
获取第i个节点的值
改变节点的值
获取节点的父节点

二叉树

定义：二叉树是每个结点最多有两个子树的树结构。

类型

完全二叉树：若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树。

满二叉树:除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树

平衡二叉树:平衡二叉树又被称为AVL树（区别于AVL算法），它是一棵二叉排序树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

二叉树的性质

(1) 在非空二叉树中，第i层的结点总数不超过  , i>=1；
(2) 深度为h的二叉树最多有  个结点(h>=1)，最少有h个结点；
(3) 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1；
(4) 具有n个结点的完全二叉树的深度为  （注：[ ]表示向下取整）；
(5)有N个结点的完全二叉树各结点如果用顺序方式存储，则结点之间有如下关系：
若I为结点编号则 如果I>1，则其父结点的编号为I/2；
如果2*I<=N，则其左孩子（即左子树的根结点）的编号为2*I；若2*I>N，则无左孩子；
如果2*I+1<=N，则其右孩子的结点编号为2*I+1；若2*I+1>N，则无右孩子。

二叉树的遍历

先序遍历：根结点 ---> 左子树 ---> 右子树

void Preorder (BiTree T) { 
	if (T) { 
		cout<<T->data;
		Preorder(T->lchild);
		Preorder(T->rchild); 
	}
}

中序遍历：左子树---> 根结点 ---> 右子树

void Inorder (BiTree T) {
	if (T) { 
		Inorder(T->lchild); 
		cout<<T->data;
    	Inorder(T->rchild);
    }

后序遍历：左子树 ---> 右子树 ---> 根结点

void Postorder (BiTree T) {
	if (T) { 
		Postorder(T->lchild); 
		Postorder(T->rchild);
		cout<<T->data;
    }
}

查找

1、顺序查找

顺序查找又叫线性查找，他的查找过程是：从表中第一个（或者最后一个）记录开始，逐个进行记录的关键字和给定值比较，若某个记录的关键字和给定值相等，者查找成功，找到所查的记录；如果直到最后一个（或者第一个）记录，其关键字和给定值比较都不等时，则表中没有所查的记录，查找不成功。

2、二分查找

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

3.分块查找

分块查找是折半查找和顺序查找的一种改进方法，分块查找由于只要求索引表是有序的，对块内节点没有排序要求，因此特别适合于节点动态变化的情况。

二叉排序树

定义
一棵空树，或者是具有下列性质的二叉树：
（1）若左子树不空，则左子树上所有结点的值均小于它的根结点的值；
（2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；
（3）左、右子树也分别为二叉排序树；
（4）没有键值相等的结点。

查找
步骤：
若根结点的关键字值等于查找的关键字，成功。
否则，若小于根结点的关键字值，递归查左子树。
若大于根结点的关键字值，递归查右子树。
若子树为空，查找不成功。

AVL树

定义：AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。

特点

1.本身首先是一棵二叉搜索树。
2.带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。
也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）

操作

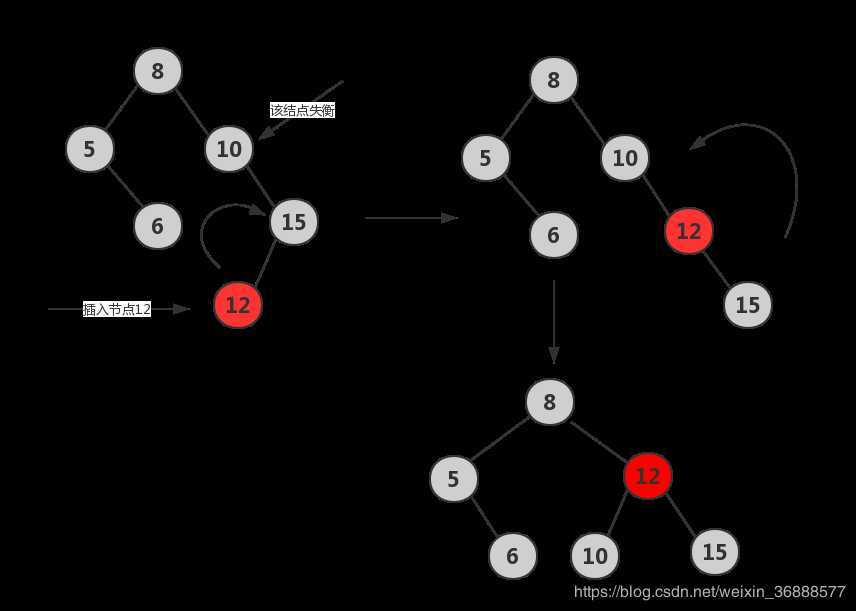
LL

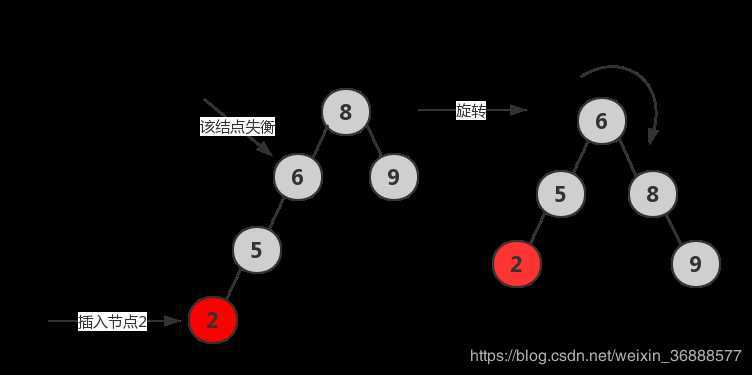
RR

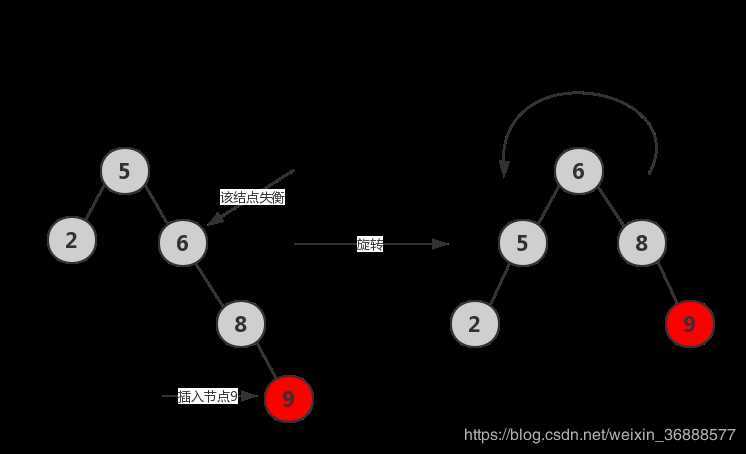
LR

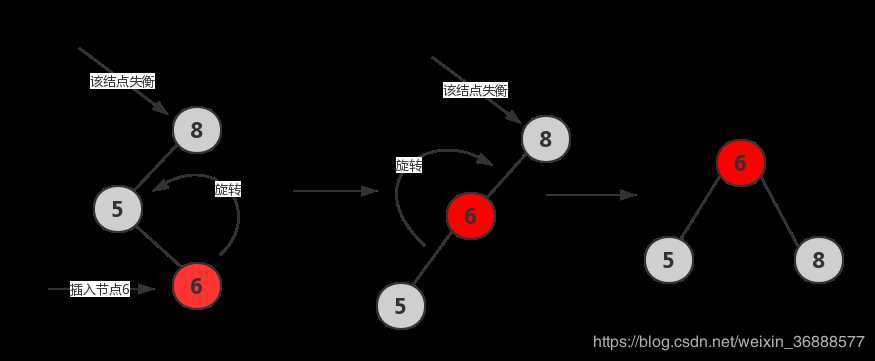
RL

哈希表

定义：是根据关键码值而直接进行访问的数据结构。也就是说，它通过把关键码值映射到表中一个位置来访问记录，以加快查找的速度。这个映射函数叫做散列函数，存放记录的数组叫做散列表。

解决哈希冲突的方法
直接定址法、数字分析法、平方取中法、折叠法、除留余数法、随机数法。

三、疑难问题及解决方案

就是在哈希表线查找不成功的平均次数计算还不懂
解决方法：上网查资料
例：

后面依次下去，所以不成功的平均次数就为：（3+2+1+2+1+5+4）/7=18/7

树、二叉树、查找总结

原文：https://www.cnblogs.com/254916-cn/p/12781134.html