数据降维在多元中的主要方法有PCA和因子分析(两者应用场景有区别)
我学过多元统计分析,更细化用矩阵思想理解,所以本篇不详细记笔记了
在很多场景中需要对多变量数据进行观测,在一定程度上增加了数据采集的工作量。更重要的是:多变量之间可能存在相关性,从而增加了问题分析的复杂性。
如果对每个指标进行单独分析,其分析结果往往是孤立的,不能完全利用数据中的信息,因此盲目减少指标会损失很多有用的信息,从而产生错误的结论。
因此需要找到一种合理的方法,在减少需要分析的指标同时,尽量减少原指标包含信息的损失,以达到对所收集数据进行全面分析的目的。由于各变量之间存在一定的相关关系,因此可以考虑将关系紧密的变量变成尽可能少的新变量,使这些新变量是两两不相关的,那么就可以用较少的综合指标分别代表存在于各个变量中的各类信息。主成分分析与因子分析就属于这类降维算法。
其最主要的用途在于“降维”,通过析取主成分显出的最大的个别差异,发现更便于人类理解的特征。也可以用来削减回归分析和聚类分析中变量的数目。
PCA的主要思想是将n维特征映射到k维上,这k维是全新的正交特征也被称为主成分,是在原有n维特征的基础上重新构造出来的k维特征。
——线代中的矩阵知识
对于如何找到一个轴,使得样本空间的所有点映射到这个轴的方差最大。
将样本进行均值归0(demean),即所有样本减去样本的均值。样本的分布没有改变,只是将坐标轴进行了移动。



在实际的降维过程可能会涉及到数据在多个维度的降维,这就需要依次求解多个主成分。
求解第一个主成分后,假设得到映射的轴为所表示的向量,如果此时需要求解第二个主成分怎么做?
答案是:需要先将数据集在第一个主成分上的分量去掉,然后在没有第一个主成分的基础上再寻找第二个主成分。
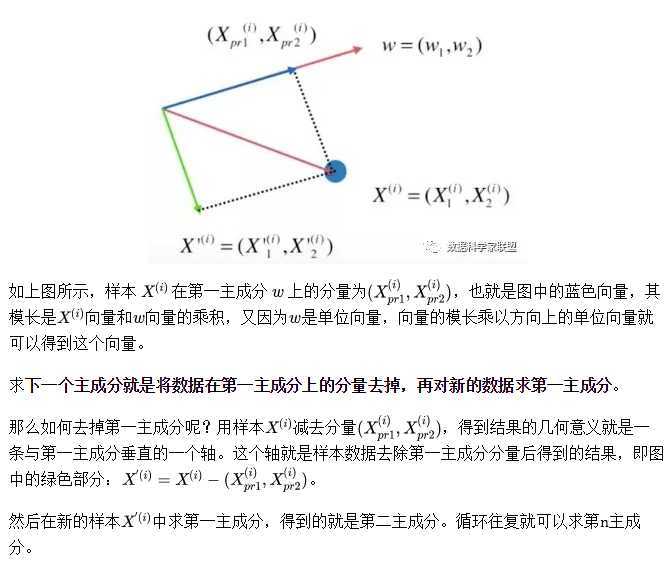
在实际的数据中不可避免地出现各种噪音,这些噪音的出现可能会对数据的准确性造成一定的影响。而主成分分析法还有一个用途就是降噪。PCA通过选取主成分将原有数据映射到低维数据再映射回高维数据的方式进行一定程度的降噪。


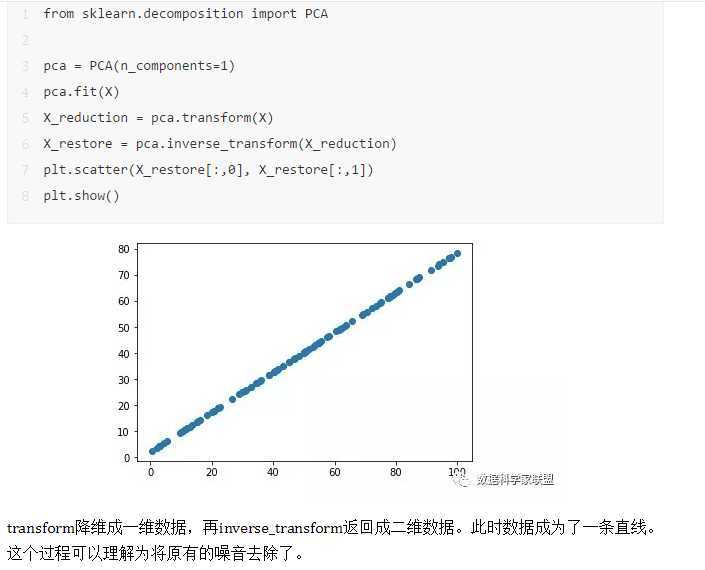

原文:https://www.cnblogs.com/wjAllison/p/12783133.html