班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈,是指所有朋友的集合。
给定一个 N * N 的矩阵 M,表示班级中学生之间的朋友关系。如果M[i][j] = 1,表示已知第 i 个和 j 个学生互为朋友关系,否则为不知道。你必须输出所有学生中的已知的朋友圈总数。
常规思路,看有多少个连通图,可以用BFS也可以用DFS
void BFS(vector<vector<int>>& M, int st, vector<bool>& vis){ queue<int> q; q.push(st); vis[st]=1; while(!q.empty()){ int t=q.front();q.pop(); for(int i=0;i<M.size();i++){ if(M[t][i]==1&&!vis[i]){ q.push(i); vis[i]=1; } } } } int findCircleNum(vector<vector<int>>& M) { int n=M.size(); if(n==0)return 0; vector<bool> vis(n,false); int ans=0; for(int i=0;i<n;i++){ if(!vis[i]){ ans++; BFS(M,i,vis); } } return ans; }
用并查集
int findCircleNum(vector<vector<int>>& M) { int n=M.size(); if(n==0)return 0; vector<int> parent(n,-1); int ans=0; for(int i=0;i<n;i++){ for(int j=i+1;j<n;j++){ if(M[i][j]==1){ int a=i,b=j; while(parent[a]!=-1)a=parent[a]; while(parent[b]!=-1)b=parent[b]; if(a!=b)parent[b]=a; } } } for(int i=0;i<n;i++){ if(parent[i]==-1)ans++; } return ans; }
在本问题中, 树指的是一个连通且无环的无向图。
输入一个图,该图由一个有着N个节点 (节点值不重复1, 2, ..., N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ,满足 u < v,表示连接顶点u 和v的无向图的边。
返回一条可以删去的边,使得结果图是一个有着N个节点的树。如果有多个答案,则返回二维数组中最后出现的边。答案边 [u, v] 应满足相同的格式 u < v。
vector<int> findRedundantConnection(vector<vector<int>>& edges) { int N=edges.size(); vector<int> parent(N+1,-1); for(int i=0;i<N+1;i++){ int a=edges[i][0],b=edges[i][1]; while(parent[a]!=-1)a=parent[a]; while(parent[b]!=-1)b=parent[b]; if(a!=b)parent[b]=a; else return {edges[i][0],edges[i][1]}; } return {-1,-1}; }
给定一个列表 accounts,每个元素 accounts[i] 是一个字符串列表,其中第一个元素 accounts[i][0] 是 名称 (name),其余元素是 emails 表示该帐户的邮箱地址。
现在,我们想合并这些帐户。如果两个帐户都有一些共同的邮件地址,则两个帐户必定属于同一个人。请注意,即使两个帐户具有相同的名称,它们也可能属于不同的人,因为人们可能具有相同的名称。一个人最初可以拥有任意数量的帐户,但其所有帐户都具有相同的名称。
合并帐户后,按以下格式返回帐户:每个帐户的第一个元素是名称,其余元素是按顺序排列的邮箱地址。accounts 本身可以以任意顺序返回。
class DSU{ vector<int> parent; public: DSU(){ parent = vector<int>(10001,0); for(int i=0;i<=10000;i++) parent[i]=i; } int find(int x){ if(parent[x]!=x) parent[x]=find(parent[x]); return parent[x]; } void un(int x, int y){ parent[find(x)]=find(y); } }; class Solution { public: vector<vector<string>> accountsMerge(vector<vector<string>>& accounts) { DSU dsu; map<string, string> emailsToName; map<string, int> emailsToId; int id = 0; for(auto& account:accounts){ string name=""; for(auto& mail:account){ if(name==""){ name=mail; continue; } if(emailsToName.count(mail)==0) emailsToName.insert({mail,name}); if(emailsToId.count(mail)==0)emailsToId[mail]=id++; dsu.un(emailsToId[account[1]],emailsToId[mail]); } } unordered_map<int, vector<string>> tmp; vector<vector<string>> ans; for(auto& mtn : emailsToName){ string mail = mtn.first;//cout<<mail<<" "; int idx=dsu.find(emailsToId[mail]); if(tmp.count(idx)>0) tmp[idx].push_back(mail); else tmp.insert({idx,{mtn.second,mail}}); } for(auto& list : tmp){ sort(list.second.begin()+1,list.second.end()); vector<string> v(list.second.begin(),list.second.end()); ans.push_back(v); } return ans; } };
在由 1 x 1 方格组成的 N x N 网格 grid 中,每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。
(请注意,反斜杠字符是转义的,因此 \ 用 "\\" 表示。)。
返回区域的数目。
示例 1:
输入: [ " /", "/ " ] 输出:2 解释:2x2 网格如下:
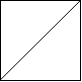
示例 2:
输入: [ " /", " " ] 输出:1 解释:2x2 网格如下:
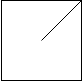
示例 3:
输入: [ "\\/", "/\\" ] 输出:4 解释:(回想一下,因为 \ 字符是转义的,所以 "\\/" 表示 \/,而 "/\\" 表示 /\。) 2x2 网格如下:
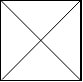
示例 4:
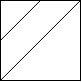
输入: [ "/\\", "\\/" ] 输出:5 解释:(回想一下,因为 \ 字符是转义的,所以 "/\\" 表示 /\,而 "\\/" 表示 \/。) 2x2 网格如下:
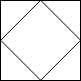
示例 5:
输入: [ "//", "/ " ] 输出:3 解释:2x2 网格如下:
提示:
1 <= grid.length == grid[0].length <= 30grid[i][j] 是 ‘/‘、‘\‘、或 ‘ ‘。
我们将N*N的大正方形,划分为N*N个1*1的小正方形,因为‘\‘和‘/‘只能将一个正方形划分为四个小三角形,我们以上方的小三角形为0,顺时针编号0,1,2,3。
那么当方格内为‘\‘时,区域0和1相连、2和3相连;当方格内为‘/‘时,0和3相连、1和2相连。同时左右相邻的小方格1和3相连,上下相邻的小方格0和2相连。
class Union{ vector<int> parent; public: Union(int n){ parent=vector<int>(n,0); for(int i=0;i<n;i++) parent[i]=i; } int find(int x){ if(parent[x]!=x) parent[x]=find(parent[x]); return parent[x]; } void un(int x, int y){ parent[find(x)]=find(y); } }; class Solution { public: int regionsBySlashes(vector<string>& grid) { int n=grid.size(); Union uf(n*n*4); for(int i=0;i<n;i++){ for(int j=0;j<n;j++){ int start=i*n*4+j*4; switch(grid[i][j]){ case ‘\\‘:{ uf.un(start+1,start); uf.un(start+2,start+3); }break; case ‘/‘:{ uf.un(start+3,start); uf.un(start+2,start+1); }break; case ‘ ‘:{ uf.un(start,start+1); uf.un(start+1,start+2); uf.un(start+2,start+3); }break; default:break; } if(i>0){ uf.un(start,start-n*4+2); } if(j>0){ uf.un(start+3,start-3); } } } int ans=0; for(int i=0;i<n*n*4;i++){ if(uf.find(i)==i)++ans; } return ans; } };
原文:https://www.cnblogs.com/Dancing-Fairy/p/12790662.html