算法是一组完成任务的指令,任何代码片段都可以视为算法。
二分查找是一种算法,其输入是一个有序的元素列表。如果要查找的元素找到,返回其位置,否则返回None.
如果是顺序查找,取决于有序列表中的元素数量n;如果是二分查找,则取决于有序列表数量n的公式 $log2^n$.
二分查找的python代码类似下面:
def binary_search(list, item):
low = 0
high = len(list)
while low <= high:
mid = (low + high) / 2
guess = list[mid]
if guess == item :
return mid
if guess > item :
high = mid - 1
else :
low = mid + 1
return None
大O表示法是一种特殊的表示法,指出了算法的运行速度有多快,它并非以时间(例如秒、毫秒)为单位的速度,而是让你能够比较操作数,它指出了算法运行时间的增速。
使用大O表示法,会指出最糟糕情况下的运行时间,下面是一些蟾宫的大O时间:
| 大O时间 | 解释 | 举例 |
|---|---|---|
| $O(log2^n)$ | 对数时间 | 二分查找 |
| $O(n)$ | 线性时间 | 简单查找 |
| $O(nlog2^n)$ | 快速排序 | |
| $O(n^2)$ | 选择排序 | |
| $O(n!)$ | 旅行商问题,非常慢的算法 |
将其进行从快到慢的依次排序:

通过大O表示法和上面的图,我们可以得到以下结论:

当你需要将数据存储到内存中时,请求计算机提供存储空间,计算机会给你一个存储地址。需要存储多项数据时,有两种基本方式——数据和链表。但它们不都适用于所有的情形,因此知道他们之间的差别很重要。
内存与硬盘的工作原理是有着巨大差别的,因此其排序方式也会有所不同,如果排序的文件处于磁盘上,且并不能一次性加载到内存中(往往内存较小),则需要考虑使用外排序。
对于数组和链表这两种非常简单的数据结构,可参考 Java数据结构与算法一篇文章。
二者常用的操作事件可以参考下面的表格:

递归描述的问题,通常是一类组合性质的问题,比如下面这种盒子套盒子,子盒子其中还可能发生嵌套的问题。
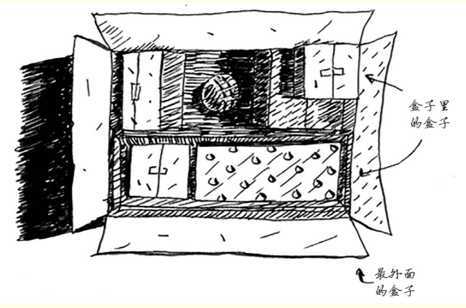
虽然这类问题可以用非递归的方式来实现(while或者无限的for循环),但更加清晰、易理解的方式其实是使用递归 —— 无限调用自己。StackOverflow上有一句话:
如果使用循环,程序的性能可能会更高;如果使用递归,程序可能更容易理解。如何选择要看什么对你更加重要”。
在递归中,为了避免调用自己时会发生无限死循环,程序必须要知道什么时候该停止,因此每个递归程序都包含两部分:
栈是一种简单的数据结构,存在着限定的访问数据方式:LIFO(Last In First Out)。
计算机在内部使用被称为调用栈的栈,在进行方法调用时,计算机会将函数调用所涉及到的所有变量的值存储到内存中(当然也会涉及到内存分配),在调用另一个函数时,当前函数暂停并处于未完成状态,所有变量值都还在内存中,直到另一个函数执行完成再回到上层的函数。
栈在递归调用中扮演着重要的角色,就像是方法调用一样。
使用栈虽然简单,但是也要付出代价:存储详尽的信息可能占用大量的内存,每个函数调用都要占用一定的内存,如果栈很高,就意味着计算机存储了大量函数调用的信息(StackOverflowError风险),有两种选择方案可以解决这个问题:
分而治之 - Divide & Conquer,是一种著名的递归式解决问题的方法,引入快速排序的目的,就是说明一下如何对问题进行分治处理,在这里分治是策略,递归是手段。
D&C的工作原理:
D&C并非可用于解决问题的算法,而是一种解决问题的思路,举个例子,为了要计算 SUM(2,4,6) 的结果,可以使用递归的方式将问题进行分解,并确定基线条件:

注意:编写涉及数组的递归函数时,基线条件通常是数组为空或只包含一个元素,陷入困境时,请检查基线条件是不是这样。
快速排序是一种常见的排序算法,要比前面介绍的选择排序快得多,C语言中的排序函数qsort()使用的就是快速排序。
其基本算法结构为:
快速排序算法实现的正确性取决于归纳证明原理,这是一种证明算法行之有效的方式,分为两步:基线条件和归纳条件。
假如,我要证明我能够爬到梯子的最上面:
下面就是快速排序的算法实现:
def quicksort(array):
if len(array) < 2:
return array
else:
pivot = array[0]
less = [i for i in array[1:] if i <= pivot]
greater = [i for i in array[1:] if i>= pivot]
return quicksort(less) + [pivot] + quicksort(greater)
print quicksort(...)
既然快速排序在最糟糕的情况下,算法复杂度退化到$O(N^2)$, 为什么不采用时间复杂度同样为$O(Nlog2^N)$的归并排序(merge sort)呢?
原因就在于算法复杂度的常量表示会有所不同,快速排序的常量要比归并排序的常量小得多,而且如果它们的运行速度都是$O(Nlog2^N)$,那么快速查找就会比归并排序快得多。
散列表是最有用的数据结构之一,用途非常广泛。
散列函数是这样的函数,无论你给他什么样的数据,都会直接返回给你一个数字,必须满足下面的要求:
散列表适合的场景:
散列表存放的数据量是有限的,尤其是当数据量比较大的情况,会发现散列后对应的数据块已经被占用,这就称为冲突:
平均情况下,散列表执行各种操作的时间均为$O(1)$;但在最糟糕的情况下,散列表的所有操作运行时间为$O(N)$,在使用散列表时,避开最糟情况至关重要,要避免冲突需要:
如下图,为找出换乘最少的路径,你该使用什么算法?

这种类型问题被称为最短路径问题(shortest-path problem),解决最短路径问题的算法被称为广度优先算法,一般此类问题需要两个步骤:
图模拟一组连接,由节点和边组成,一个节点可能会与众多节点直接相连,这些节点被称为邻居,所以图一般是用来模拟不同的东西是如何相连的。
广度优先搜索是一种用于图的查找,方便解决下面的两类问题:
队列:与现实生活中的队列原理类似,与栈比较相近,你不能随机地访问队列中的元素,它只支持两种操作:入队和出队;
队列是一种先进先出(FIFO)的数据结构,而栈是一种后进先出(LIFO)的数据结构。
假设你经营着一个芒果农场,需要寻找芒果销售商,以便将芒果卖给他。在Facebook,你与 芒果销售商有联系吗?为此,你可在朋友中查找。
借助队列实现的算法思路为:

def search(name):
search_queue = deque()
search_queue += graph[name]
searched = []
while search_queue:
person = search_queue.popleft()
if not person in searched:
if person_is_seller(person):
print person + " is a mongo seller!"
return True
else
search_queue += graph[person]
searched.append(person)
return False
这个算法将不断执行,直到满足以下条件之一:
前一章中的图是否存在路径,采用的是广度优先搜索算法,它找出的是段数最少的路径。如果你想要找到最快的路径,可以考虑使用另外一种算法 —— 迪克斯特拉算法。

这种带有权重边的图被称为加权图(不带权重的图被称为非加权图),其中包含4个主要步骤:
要计算加权图的最短路径,使用广度优先搜索;要计算非加权图的最短路径,使用迪克斯特拉算法。当然,迪克斯特拉只适用于有向无环图。
总体算法如下:

以伪代码方式:
node = find_lowest_cost_node(costs)
while node is not None: //结束条件:所有节点都被处理过
cost = costs[node]
neighbours = graph[node]
for n in neighbours.keys():
new_cost = cost + neighbours[n]
if costs[n] > new_cost:
costs[n] = new_cost
parents[n] = n
proceeded.append(node)
node = find_lowest_code_node(costs)
def find_lowest_cost_node(costs):
lowest_cost = float("inf")
lowest_cost_node = None
for node in costs: // 遍历所有节点
cost = costs[node]
if cost < lowest_code and node not in processed: //如果当前节点成本更低且没有被使用过
lowest_cost = cost //将其设置成开销最低的节点
lowest_cost_node = node
return lowest_cost_node
假如有如下问题,你希望将尽可能多的课程安排在某间教室,如何选出尽可能多且时间不冲突的课程呢?

具体做法可能比较简单:
1.选出最早结束的课,这就是在这间教室上的第一节课;
2.接下来,选择第一节课结束后开始的最早结束的课,这是第二节课,以此类推;
从算法实现和原理上来看,贪婪算法太容易、太显而易见,这正是贪婪算法的优点:简单易行!贪婪算法很简单:每步都采用最优的做法,用专业术语来说,就是每步都选择局部最优解,最终得到的就是全局最优解。
显然,贪婪算法并不是在所有情况下都行之有效,但它简单易行!
对于不可切分物品的背包问题,贪婪算法显然不能获得最优解,但非常接近。这给我们一个启示:在有些情况下,完美是优秀的敌人,有时候你只需要找到一个能够大致解决的算法,此时,贪婪算法就可以派上用场了,因为他们实现起来很容易,得到的结果又与正确结果大致接近。
又假设你办了个广播节目,想让全美50个州的听众都能够收听地到,为此你决定要在哪些广播台中播出。因为每个广播台都需要费用,你需要力图在尽可能少的广播台播出。
每个广播台都有其覆盖的区域,不同广播台之间可能会有所交叉。

简单的方案可能如下:
由于可能的子集会有$2N$个,所以运行时间为$O(2N)$,这个部分的工作量非常大,有没有合适的算法来解决这个问题呢?借助于近似算法。
使用下面的贪婪算法可以得到非常接近的解:
这就是一种近似算法,在获得精确解需要的时间太长时,可使用近似算法,判断其优劣的标准为:
在这里例子中,贪婪算法的运行时间为$O(N^2)$.
旅行商问题,所有可能的路线,被称为阶乘函数,其复杂度为$O(N!)$,涉及到的城市非常多的时候,根本没有办法解决。
对于旅行商问题,什么样的近似算法是不错的呢?能找到较短路径的算法就不错。NP完全问题的简单定义是,以难解著称的问题,很多聪明人都认为,根本不可能写出可以快速解决这些问题的方法。
但要判断出某一问题属于NP完全问题就比较难,易于解决的问题和NP完全问题的差别通常很小。虽然很难,但还是有一些蛛丝马迹可循的:
动态规划算法的工作原理:先解决子问题,再逐步解决大问题。

在解决该问题时,动态规划逐步计算最大价值,其转移公式类似下面:

动态规划是从小问题入手,逐步解决大问题,这里解决的小问题会帮助解决大问题。
假设行窃时可以偷走的是成袋的米和面,整袋装不下可以将包装打开,再将背包填满,这种情况是无法用动态规划来实现的。
但是使用贪婪算法可以轻松地解决这个问题!首先,先尽可能多地拿价值最高的产品;然后,再去拿价值次高的产品;以此类推即可。
原文:https://www.cnblogs.com/zhiqiangma/p/12790914.html