题意:在一个平面直角坐标系,一个点总是从原点出发,但是每次移动只能移动8个方向的中的一个并且每次移动距离
只有1和√2这两种情况,最后一定会回到原点(以字母5结束),请你计算这个点所画出图形的面积
题解:
叉积又叫向量积,如下图
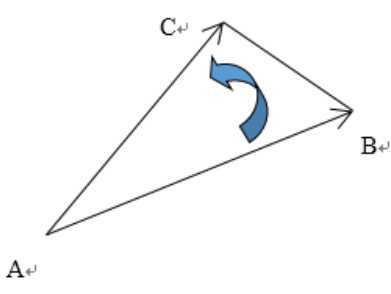
设AC这条边为向量a,AB这条边为向量b,夹角为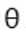
那么会有: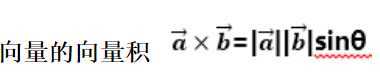

那么一个多边形肯定是可以分解成多个三角形的,把它们的面积加到一起就行了
我们知道三角形的角度不是那么容易就可以求出来的,而且通过向量坐标也可以求向量积的模(下面给出三维模式下的)

二位模式下:
向量a=(x1,y1),向量b=(x2,y2)
(向量a*向量b)的模=x1*y2-x2*y1
代码:

1 #include<stdio.h> 2 #include<string.h> 3 #include<iostream> 4 #include<algorithm> 5 #include<math.h> 6 #include<vector> 7 #include<queue> 8 #include<stack> 9 #include<map> 10 using namespace std; 11 typedef long long ll; 12 const int maxn=1e6+10; 13 const int INF=0x3f3f3f3f; 14 const double eps=1e-8; 15 const double PI=3.1415926; 16 const int mod = 1e9+7; 17 #define mt(A,B) memset(A,B,sizeof(A)) 18 #define lson l,m,rt*2 19 #define rson m+1,r,rt*2+1 20 #define SIS std::ios::sync_with_stdio(false),cin.tie(0),cout.tie(0) 21 #define zero(x) (((x)>0?(x):-(x))<eps) 22 int dir[8][2]={{0,1},{0,-1},{1,0},{-1,0},{1,1},{-1,1},{1,-1},{-1,-1}};//8个方向 23 char str[maxn]; 24 int main() 25 { 26 int T; 27 int n,m,i,j; 28 int x,y,u,v; 29 long long A; 30 cin>>T; 31 while(T--) 32 { 33 cin>>str; 34 n=strlen(str); 35 x=0; 36 y=0; 37 A=0; 38 for(i=0;i<(n-1);i++) 39 { 40 if(str[i]==‘8‘) 41 { 42 u=x+dir[0][0]; 43 v=y+dir[0][1]; 44 } 45 else if(str[i]==‘2‘) 46 { 47 u=x+dir[1][0]; 48 v=y+dir[1][1]; 49 } 50 else if(str[i]==‘6‘) 51 { 52 u=x+dir[2][0]; 53 v=y+dir[2][1]; 54 } 55 else if(str[i]==‘4‘) 56 { 57 u=x+dir[3][0]; 58 v=y+dir[3][1]; 59 } 60 else if(str[i]==‘9‘) 61 { 62 u=x+dir[4][0]; 63 v=y+dir[4][1]; 64 } 65 else if(str[i]==‘7‘) 66 { 67 u=x+dir[5][0]; 68 v=y+dir[5][1]; 69 } 70 else if(str[i]==‘3‘) 71 { 72 u=x+dir[6][0]; 73 v=y+dir[6][1]; 74 } 75 else if(str[i]==‘1‘) 76 { 77 u=x+dir[7][0]; 78 v=y+dir[7][1]; 79 } 80 A+=(u*y)-(v*x);//(u,v),(x,y)和(0,0)原点的叉积算出三角形的面积 81 x=u; 82 y=v; 83 } 84 if(A<0)//顺时针计算是负值 85 A=-A; 86 if(A%2==0)//如果面积可以整除2那么不会有精度缺失 87 cout<<A/2<<endl; 88 else//否则要加上0.5 89 cout<<A/2<<".5"<<endl; 90 } 91 return 0; 92 }
POJ - 1654 利用叉积求三角形面积 去 间接求多边形面积
原文:https://www.cnblogs.com/kongbursi-2292702937/p/12797633.html