龙贝格算法主要是不断递推和加速,直到满足精度要求
递推:
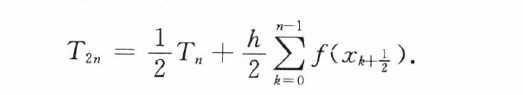
加速:
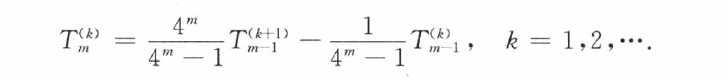
得到T表:
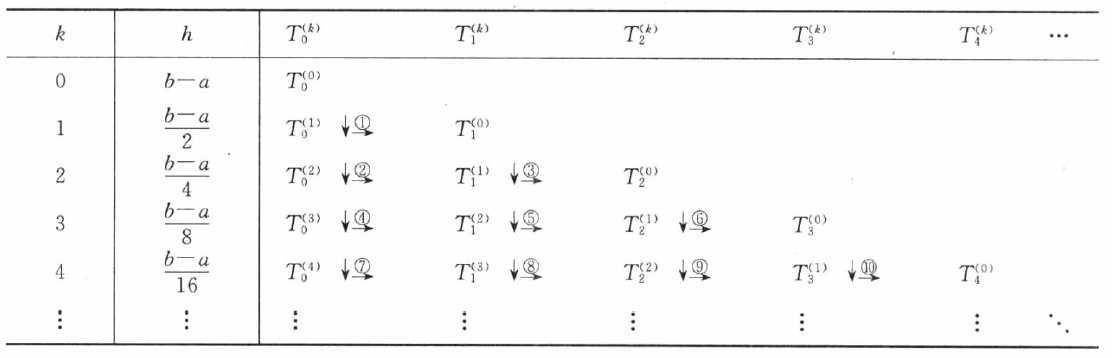
MATLAB代码:
function I = Romberg(f, a, b, epsion)
I = 0;
h = b-a;
k = 0;
m = 0;
T = zeros(5);
%下标转换:T^(k)_0 => T(k+1,1)
T(1,1) = h/2 * (subs(f,a) + subs(f,b));%即T^(0)_0
delta = 2*epsion;
while delta > epsion
k = k + 1;
h = h / 2;
tmpSum = 0; j = a + h;
while j < b
tmpSum = tmpSum + subs(f, j);
j = j + 2*h;
end
T(k+1, 1) = 0.5*T(k, 1) + h*tmpSum;
j = 2;
while j <= k+1
T(k+1,j) = (4^(j-1)*T(k+1,j-1) - T(k, j-1)) / (4^(j-1)-1);
j = j + 1;
end
delta = abs(T(k+1, k+1) - T(k, k));
end
I = T(k+1,k+1);
T
end
此代码对于f(x)=xsin(x), 积分端点又是0和2pi时,计算出的T会全为零,需要把外循环条件改为 delta > epsion | sum(T) == 0
原文:https://www.cnblogs.com/yl-xy/p/12801362.html