【Kaggle-数据分析竞赛】House Price Prediction 项目总结

Kaggle-数据分析竞赛：House Price Prediction官网链接

1. 项目概述

• 项目背景：影响房屋价格的因素众多，如房屋面积、房屋层数、配套设施等等。
• 项目要求：利用竞赛提供的数据，通过分析影响房屋价格的诸多因素来对房屋价格进行预测。
• 项目数据：项目数据分成训练数据（train.txt）和测试数据（test.txt），其中字段” LotConfig”、“ LandSlope”等79个字段是特征变量（不包括ID列），”SalePrice”字段是目标变量。
• 评估指标：本项目结果评估指标为均方根误差（Root Mean Squared Error, RMSE）。

2. 项目思路

该项目的基本思路如下图所示。项目所有流程均基于Python实现。

3. 问题定义

该项目要求利用给定的数据（共包括81个特征，数值型特征和类别型特征均有）来对房屋价格进行预测，因此考虑采用回归方法进行预测。同时，为了提高预测的准确率（尽量降低RMSE），考虑基于集成学习思想的多个回归模型集成方法。

4. 数据观察

• 利用Python第三方库pandas_profiling对训练集生成描述性统计报告。发现该数据中包含数值型特征和类别型特征，大量特征存在缺失值。缺失率可视化如下图所示：
  

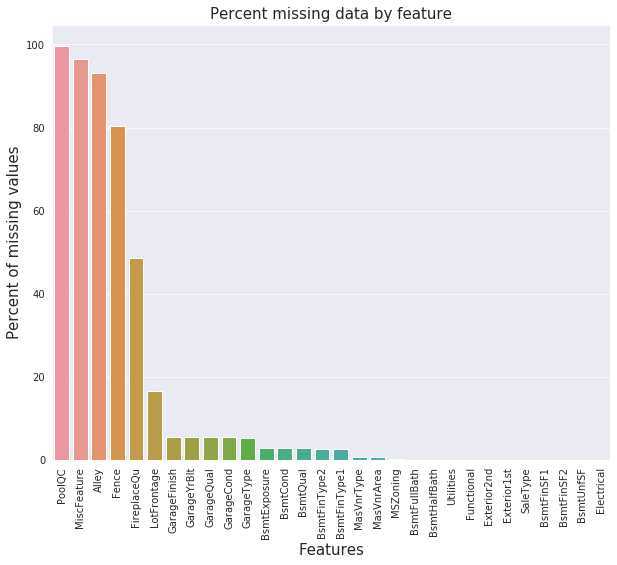
• 通过数据分布可视化，发现数据在许多特征上存在偏态性。以训练集目标变量SalePrice为例，数据分布及QQ图如下图所示：
  

5. 数据预处理

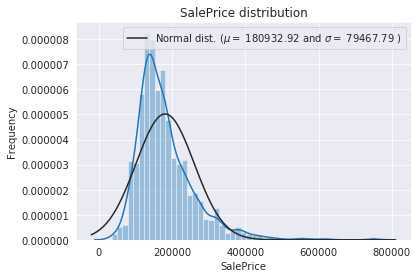
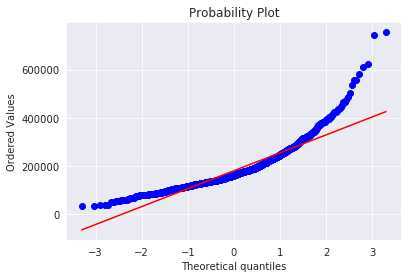
• 异常值处理：选择对房屋价格影响较大的面积变量"GrLivArea"与目标变量 "SalePrice"的关系进行数据可视化（散点图），可以看到存在两个明显的异常值点（房屋面积极大但是房价极低，不符合业务常识），如下图所示：
  
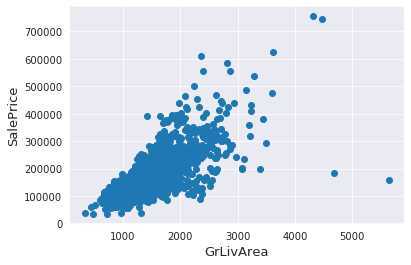
  对这两个异常值点进行删除。

• 缺失值处理：根据竞赛提供的特征变量的解释，充分理解每个特征的含义，综合采用众数、中位数等方法进行缺失值填补。

• 数据偏态处理：通过观察每个数值型特征的数据分布，对目标变量SalePrice采用对数化处理；对其余特征变量采用Box-Cox转换处理。以SalePrice变量为例，偏态处理后的数据分布及QQ图如下图所示（经过处理后的数据更符合回归问题要求的正态分布）：
  

6. 特征工程

• 根据业务常识，由于面积是影响房屋价格的主要因素，所以基于现有的有关面积的特征变量：TotalBsmtSF、1stFlrSF、2stFlrSF生成新的面积加总变量TotalSF变量。
• 对于部分数值型特征，其表达的含义其实是类别信息，因此将这些特征转化为类别型数据，如MSSubClass（房屋等级类别）等。
• 对于包含排序信息的类别型特征，为了充分保留其排序信息，对这些特征采用LabelEncoder变换。

7. 多模型训练

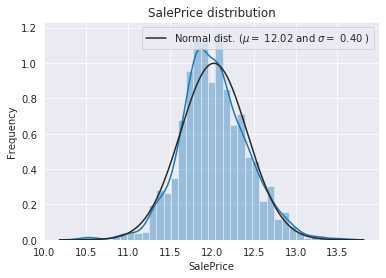
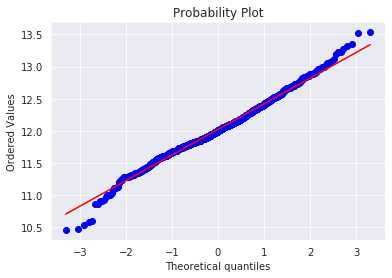
对于该回归问题，本项目选择的模型有：

通过K折交叉验证计算上述模型的RMSE的均值和标准差。

8. 集成学习

对训练好的多模型进行集成融合，生成最终的模型Stacking model。

9. 预测

分别用Stacking model、XGBregreressor、LGBMRegressor对测试集进行预测，然后将三个预测结果进行加权，得到最终结果：

【Kaggle-数据分析竞赛】House Price Prediction 项目总结

原文：https://www.cnblogs.com/yangzhehan/p/12809171.html