学会运用Mathematica、Lingo或Matlab软件求解非线性规划模型。
实验步骤要有模型建立,模型求解、结果分析。
(1)某厂向用户提供发动机,合同规定,第一、二、三季度末分别交货40台、60台、80台.每季度的生产费用为f(x)=ax+bx2(元),其中x是该季生产的台数.若交货后有剩余,可用于下季度交货,但需支付存储费,每台每季度c元.已知工厂每季度最大生产能力为100台,第一季度开始时无存货,设a=50、b=0.2、c=4,问工厂应如何安排生产计划,才能既满足合同又使总费用最低.讨论a、b、c变化对计划的影响,并作出合理的解释。
(2)一基金管理人的工作是,每天将现有的美元、英镑、马克、日元四种货币按当天汇率相互兑换,使在满足需要的条件下,按美元计算的价值最高.设某天的汇率、现有货币和当天需求如下:
|
|
美元 |
英镑 |
马克 |
日元 |
现有量 |
需求量 |
|
美元 |
1 |
.58928 |
1.743 |
138.3 |
8 |
6 |
|
英镑 |
1.697 |
1 |
2.9579 |
234.7 |
1 |
3 |
|
马克 |
.57372 |
.33808 |
1 |
79.346 |
8 |
1 |
|
日元 |
.007233 |
.00426 |
.0126 |
1 |
0 |
10 |
问该天基金管理人应如何操作(“按美元计算的价值”指兑入、兑出汇率的平均值,如1英镑相当于(1.697+(1/0.58928))/2=1.696993美元).

使用Lingo求解:

1 model: 2 min=50*x1+0.2*(x1^2)+4*(x1-40)+50*x2+0.2*(x2^2)+4*(x1+x2-100)+50*x3+0.2*(x3^2); 3 x1>=40; 4 (x1-40)+x2>=60; 5 (x1-40)+x2-60+x3=80; 6 0<=x1;x1<=100; 7 0<=x2;x2<=100; 8 0<=x3;x3<=100; 9 @gin(x1); 10 @gin(x2); 11 @gin(x3); 12 end
运行截图:
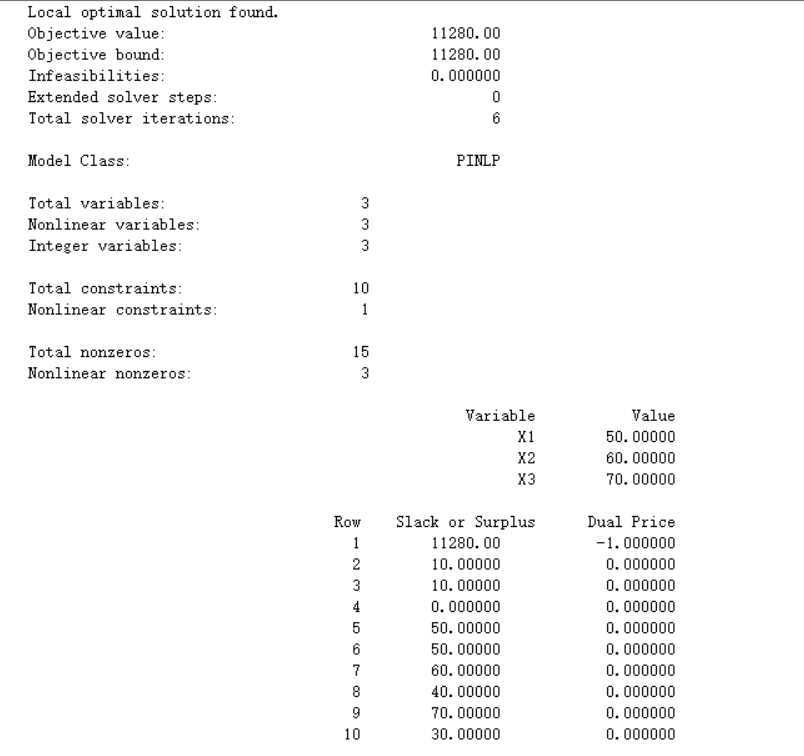
使用Mathematica求解,

1 (*非线性一,1*) 2 Minimize[{50*Subscript[x, 1]+0.2*\!\(\*SubsuperscriptBox[\(x\), \(1\), \(2\)]\)+4*(Subscript[x, 1]-40)+50*Subscript[x, 2]+0.2*\!\(\*SubsuperscriptBox[\(x\), \(2\), \(2\)]\)+4*(Subscript[x, 1]+Subscript[x, 2]-100)+50*Subscript[x, 3]+0.2*\!\(\*SubsuperscriptBox[\(x\), \(3\), \(2\)]\), 3 Subscript[x, 1]>=40,Subscript[x, 1]-40+Subscript[x, 2]>=60,Subscript[x, 1]-40+Subscript[x, 2]-60+Subscript[x, 3]==80, 4 0<=Subscript[x, 1] && Subscript[x, 1]<=100,0<=Subscript[x, 2] && Subscript[x, 2]<=100,0<=Subscript[x, 3] && Subscript[x, 3]<=100, 5 Subscript[x, 1]\[Element]Integers,Subscript[x, 2]\[Element]Integers,Subscript[x, 3]\[Element]Integers 6 },{Subscript[x, 1],Subscript[x, 2],Subscript[x, 3]}]
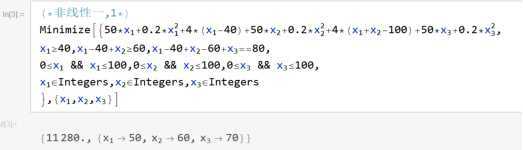
使用MATLAB求解,

1 %电动机生产的非线性规划问题 2 %目标函数 3 H=[0.4 0 0;0 0.4 0;0 0 0.4];%二次项 4 c=[58;54;50];%一次项 5 %约束条件 6 A=[1 0 0;1 1 0;];%不等式项 7 b=[40;100]; 8 Aeq=[1 1 1];%使用时取负,使得不等式符号改变 9 beq=[180]; 10 [x,z]=quadprog(H,c,-A,-b,Aeq,beq,[0;0;0],[100;100;100]); 11 x 12 z-560%把常数项减掉

解得第一季度生产50台发动机,第二季度生产60台发动机,第三季度生产70台发动机,所花总成本最小,为11280元。

使用Lingo求解,

1 model: 2 sets: 3 row/1..4/:v,n; 4 Links(row,row):r; 5 endsets 6 data: 7 v=8,1,8,0; 8 n=6,3,1,10; 9 r=1,0.58928,1.743,138.3, 10 1.697,1,2.9579,234.7, 11 0.57372,0.33808,1,79.346, 12 0.007233,0.00426,0.0126,1; 13 enddata 14 y1=(r(2,1)+1/r(1,2))/2; 15 y2=(r(3,1)+(1/r(1,3)))/2; 16 y3=(r(4,1)+(1/r(1,4)))/2; 17 max=x1+x2*r(1,2)*y1+x3*r(1,3)*y2+x4*r(1,4)*y3+x5*r(2,1)+x6*y1+x7*r(2,3)*y2+x8*r(2,4)*y3+x9*r(3,1)+x10*r(3,2)*y1+x11*y2+x12*r(3,4)*y3; 18 x1+x2+x3+x4=8; 19 x5+x6+x7+x8=1; 20 x9+x10+x11+x12=8; 21 x1+r(2,1)*x5+r(3,1)*x9>=6; 22 r(1,2)*x2+x6+r(3,2)*x10>=3; 23 r(1,3)*x3+r(2,3)*x7+x11>=1; 24 r(1,4)*x4+r(2,4)*x8+r(3,4)*x12>=10; 25 end
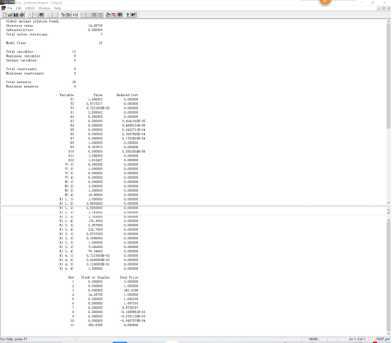
使用Mathematica求解

1 (*非线性一,2*) 2 Maximize[{Subscript[x, 1]+Subscript[x, 2]*0.58928*1.69699+Subscript[x, 3]*1.743*0.573722+Subscript[x, 4]*138.3*0.00723183+ 3 Subscript[x, 5]*1.697+Subscript[x, 6]*1.69699+Subscript[x, 7]*2.9579*0.573722+Subscript[x, 8]*234.7*0.00723183+Subscript[x, 9]*0.57372+Subscript[x, 10]*0.33808*1.69699+ 4 Subscript[x, 11]*0.573722+Subscript[x, 12]*79.346*0.00723183, 5 Subscript[x, 1]+Subscript[x, 2]+Subscript[x, 3]+Subscript[x, 4]==8, 6 Subscript[x, 5]+Subscript[x, 6]+Subscript[x, 7]+Subscript[x, 8]==1, 7 Subscript[x, 9]+Subscript[x, 10]+Subscript[x, 11]+Subscript[x, 12]==8, 8 Subscript[x, 1]+1.697*Subscript[x, 5]+0.57372*Subscript[x, 9]>=6, 9 0.58928*Subscript[x, 2]+Subscript[x, 6]+0.33808*Subscript[x, 10]>=3, 10 1.743*Subscript[x, 3]+2.9579*Subscript[x, 7]+Subscript[x, 11]>=1, 11 138.3*Subscript[x, 4]+234.7*Subscript[x, 8]+79.346*Subscript[x, 12]>=10, 12 Subscript[x, 1]>=0,Subscript[x, 2]>=0,Subscript[x, 3]>=0,Subscript[x, 4]>=0,Subscript[x, 5]>=0,Subscript[x, 6]>=0,Subscript[x, 7]>=0,Subscript[x, 8]>=0,Subscript[x, 9]>=0,Subscript[x, 10]>=0,Subscript[x, 11]>=0,Subscript[x, 12]>=0 13 },{Subscript[x, 1],Subscript[x, 2],Subscript[x, 3],Subscript[x, 4],Subscript[x, 5],Subscript[x, 6],Subscript[x, 7],Subscript[x, 8],Subscript[x, 9],Subscript[x, 10],Subscript[x, 11],Subscript[x, 12]}]

结果为,

未知量的设置应该尽量减小目标函数的复杂程度,能使用一元的就不使用多元,能使用一次方程的就使用一次方程,能使用多项式的就不使用带对数或三角函数的方程。在编程解决问题时,必须考虑式子的灵敏度,误差限。
原文:https://www.cnblogs.com/jianle23/p/12815405.html