
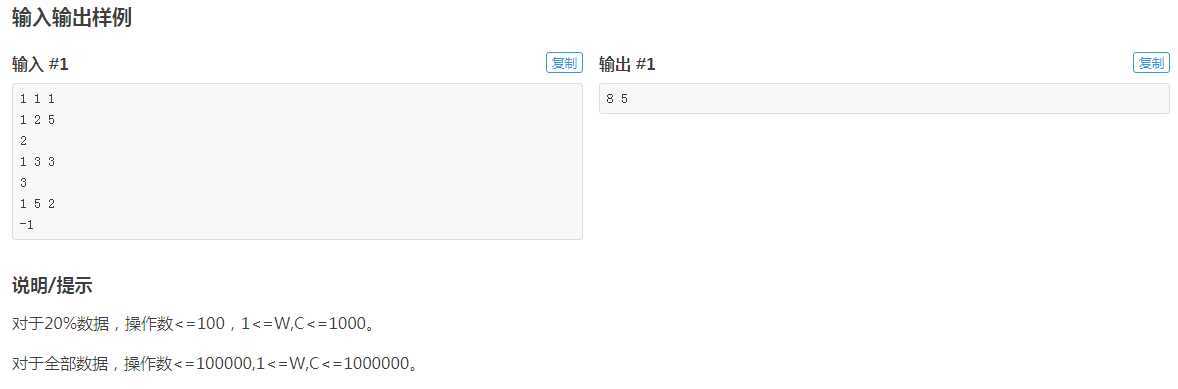
因为c保证只会出现一次并且c小于等于106
我们可以以c为关键字,维护花费和优美度,构建一棵线段树
对于1操作,我们直接查询c节点是否有值,有就直接返回,反之赋值
对于2操作,删去最大值,就从完整区间开始,只要右子树有点或左子树无点,就尽可能的去遍历右儿子,否则才遍历左儿子,将最后到达的叶子节点清零
对于3操作,删去最小值,就从完整区间开始,只要左子树有点,就尽可能的去遍历左儿子,否则才遍历右儿子,将最后到达的叶子节点清零
最后输出整个区间的总优美度和总花费就行
代码:
#include<cmath> #include<cstdio> #include<cstring> #include<algorithm> #define ls id<<1 #define rs id<<1|1 using namespace std; const int maxn=1e6+10; const int INF=0x7f7f7f7f; int opt; bool vis[maxn]; struct Tree { int l,r; int sumw,sumc; int minn,maxx; }tree[maxn<<2]; void build(int id,int ll,int rr) { tree[id].l=ll,tree[id].r=rr,tree[id].minn=INF; if(ll==rr) return; int m=ll+rr>>1; build(ls,ll,m),build(rs,m+1,rr); } void update(int id,int pos,int val1,int val2,int val3,int val4) { if(tree[id].l==pos && tree[id].r==pos) { tree[id].sumc=val1;tree[id].sumw=val2; tree[id].minn=val3;tree[id].maxx=val4; return; } if(tree[ls].r>=pos) update(ls,pos,val1,val2,val3,val4); else update(rs,pos,val1,val2,val3,val4); tree[id].sumc=tree[ls].sumc+tree[rs].sumc; tree[id].sumw=tree[ls].sumw+tree[rs].sumw; tree[id].minn=min(tree[ls].minn,tree[rs].minn); tree[id].maxx=max(tree[ls].maxx,tree[rs].maxx); } int main() { int n=maxn-10; build(1,1,n); while(scanf("%d",&opt)==1&&opt!=-1) { int w,c; if(opt==1) { scanf("%d%d",&w,&c); if(vis[c]) continue; update(1,c,c,w,c,c); vis[c]=true; } if(opt==3) { if(tree[1].minn==INF) continue; vis[tree[1].minn]=false,update(1,tree[1].minn,0,0,INF,0); } if(opt==2) { if(tree[1].maxx==0) continue; vis[tree[1].maxx]=false,update(1,tree[1].maxx,0,0,INF,0); } } printf("%d %d",tree[1].sumw,tree[1].sumc); }
当然也可以运用平衡树的有关知识
将Splay运用的精确一些
就是fhq−Treap
对于插入操作,假设权值为k。我们按照权值先split出小于等于k的一棵树x,再把x split 出小于等于k−1 的一棵树 y。如果 y 这棵子树不为空,也就是说已经有了权值为k 的节点,那么我们不插入即可。
对于删除操作,我们可以按照子树大小split 出我们要删除的值,然后不merge 即可。
最后 dfs 一遍求出答案即可。
贴一份有关这方面的代码(不是我写的)
#include<cstdio> #include<cstdlib> #define N 100005 #define int long long int tot,Root; int ans1,ans2; int beauty[N]; int val[N],sze[N]; int ch[N][2],prio[N]; void pushup(int o){ sze[o]=sze[ch[o][0]]+sze[ch[o][1]]+1; } void split(int o,int k,int &x,int &y){ if(!o) x=y=0; else{ if(sze[ch[o][0]]>=k){ y=o; split(ch[o][0],k,x,ch[o][0]); pushup(o); } else{ x=o; split(ch[o][1],k-sze[ch[o][0]]-1,ch[o][1],y); pushup(o); } } } int merge(int x,int y){ if(!x or !y) return x+y; if(prio[x]<prio[y]){ ch[x][1]=merge(ch[x][1],y); pushup(x); return x; } else{ ch[y][0]=merge(x,ch[y][0]); pushup(y); return y; } } void split2(int o,int k,int &x,int &y){ if(!o) x=y=0; else{ if(val[o]<=k){ x=o; split2(ch[o][1],k,ch[o][1],y); } else{ y=o; split2(ch[o][0],k,x,ch[o][0]); } pushup(o); } } int newnode(int a,int b){ sze[++tot]=1; prio[tot]=rand(); beauty[tot]=a; val[tot]=b; return tot; } void insert(int o,int a,int b){ int x,y,z; split2(Root,b,x,y); split2(x,b-1,x,z); if(sze[z]!=0) Root=merge(x,merge(z,y)); else Root=merge(x,merge(newnode(a,b),y)); } void delex(){ int siz=sze[Root]; int a; split(Root,siz-1,Root,a); } void delch(){ int a; split(Root,1,a,Root); } void dfs(int now){ if(!now) return; ans1+=beauty[now]; ans2+=val[now]; dfs(ch[now][0]); dfs(ch[now][1]); } signed main(){ int opt,a,b; while(scanf("%lld",&opt)){ if(opt==-1) break; if(opt==1){ scanf("%lld%lld",&a,&b); insert(Root,a,b); } if(opt==2) delex(); if(opt==3) delch(); } dfs(Root); printf("%lld %lld\n",ans1,ans2); return 0; }
原文:https://www.cnblogs.com/gongcheng456/p/12819862.html