爬山,有n个检查点,给出检查点的高度,如果一个检查点高于左边的并且高于右边的(最左边和最右边的检查点默认不是),就算作山峰,求山峰的数量。
扫一遍就好了
#include<bits/stdc++.h>
using namespace std;
const int MAX=105;
int a[MAX];
int main()
{
int T,cas=0;
cin>>T;
while(T--)
{
int n,ans=0;
cin>>n;
for(int i=0;i<n;i++)
cin>>a[i];
for(int i=1;i<n-1;i++)
if(a[i]>a[i-1]&&a[i]>a[i+1])ans++;
cout<<"Case #"<<++cas<<": "<<ans<<endl;
}
}
有n个bus,按顺序乘坐,但是第i个bus只能在xi或者xi的倍数的天乘坐,有一个人想在D天内坐完所有bus,并且越完开始越好,求最晚可以在第几天开始,使得这个人可以在D天内坐完所有bus。
D很大,n很小,所以二分答案,每次check O(n)解决,总体O(nlogD)
#include<bits/stdc++.h>
using namespace std;
const int MAX=1e3+3;
typedef long long ll;
int n;
ll x[MAX],d;
bool check(ll s)
{
for(int i=0;i<n;i++)
{
if(s%x[i]==0)continue;
s=x[i]*(s/x[i]+1);
if(s>d)return 0;
}
return 1;
}
int main()
{
int T,cas=0;
scanf("%d",&T);
while(T--)
{
scanf("%d%lld",&n,&d);
for(int i=0;i<n;i++)
scanf("%lld",&x[i]);
ll L=1,R=d,res;
while(L<=R)
{
ll m=(L+R)>>1;
if(check(m))
{
res=m;
L=m+1;
}
else R=m-1;
}
printf("Case #%d: %lld\n",++cas,res);
}
}
给一个1e9 x 1e9的矩阵,边界相邻(1再往左走走到1e9),机器人初始位于(1,1),再给出一个指令序列,有EWSN几种指令,代表向东/西/南/北走一格。指令序列还有可能有x(y),代表括号内指令y执行x次。求执行完指令序列后机器人的位置。
模拟,括号指令递归处理一下(递归时处理一下括号匹配),值得注意的地方是 要先计算每次递归总体移动的x,y值返回,最后再计算,否则会超时,还有就是过程中记得取模。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef pair<ll,ll> pll;
const int MAX=2e3+3;
const ll mod=1e9;
char s[MAX];
ll curx,cury;
ll dx[4]= {1,0,-1,0};
ll dy[4]= {0,1,0,-1};
int check(char c)
{
int idx;
if(c==‘E‘)idx=0;
if(c==‘S‘)idx=1;
if(c==‘W‘)idx=2;
if(c==‘N‘)idx=3;
return idx;
}
pll slove(int num,int l,int r)
{
ll totx=0,toty=0;
for(int i=l; i<r; i++)
{
int cur=s[i]-‘0‘;
if(cur>=2&&cur<=9)
{
int ed,tot=-1;
for(int j=i+2; j<r; j++)
{
if(s[j]==‘)‘)tot++;
if(s[j]==‘(‘)tot--;
if(tot==0)
{
ed=j;
break;
}
}
pll res=slove(cur,i+2,ed);
totx+=res.first;
toty+=res.second;
i=ed;
}
else
{
int idx=check(s[i]);
totx+=dx[idx];
toty+=dy[idx];
}
}
totx=(((totx+mod)%mod)*num+mod)%mod;
toty=(((toty+mod)%mod)*num+mod)%mod;
return make_pair(totx,toty);
}
int main()
{
int T,cas=0;
scanf("%d",&T);
while(T--)
{
scanf("%s",s);
int len=strlen(s);
pll res=slove(1,0,len);
printf("Case #%d: %lld %lld\n",++cas,(res.first+mod)%mod+1,(res.second+mod)%mod+1);
}
}
给一个n*m的矩阵,中间有一个矩形的坑,一个机器人初始在(1,1)点,每次只能向右或向下走,若位于最右边,则只能向下,若位于最下部,则只能向右,一般位置则等概率随机向右或向下,求能从(1,1)走到(n,m)的概率
test1可以用动态规划解决,但是test2数据范围太大,不能用动态规划。
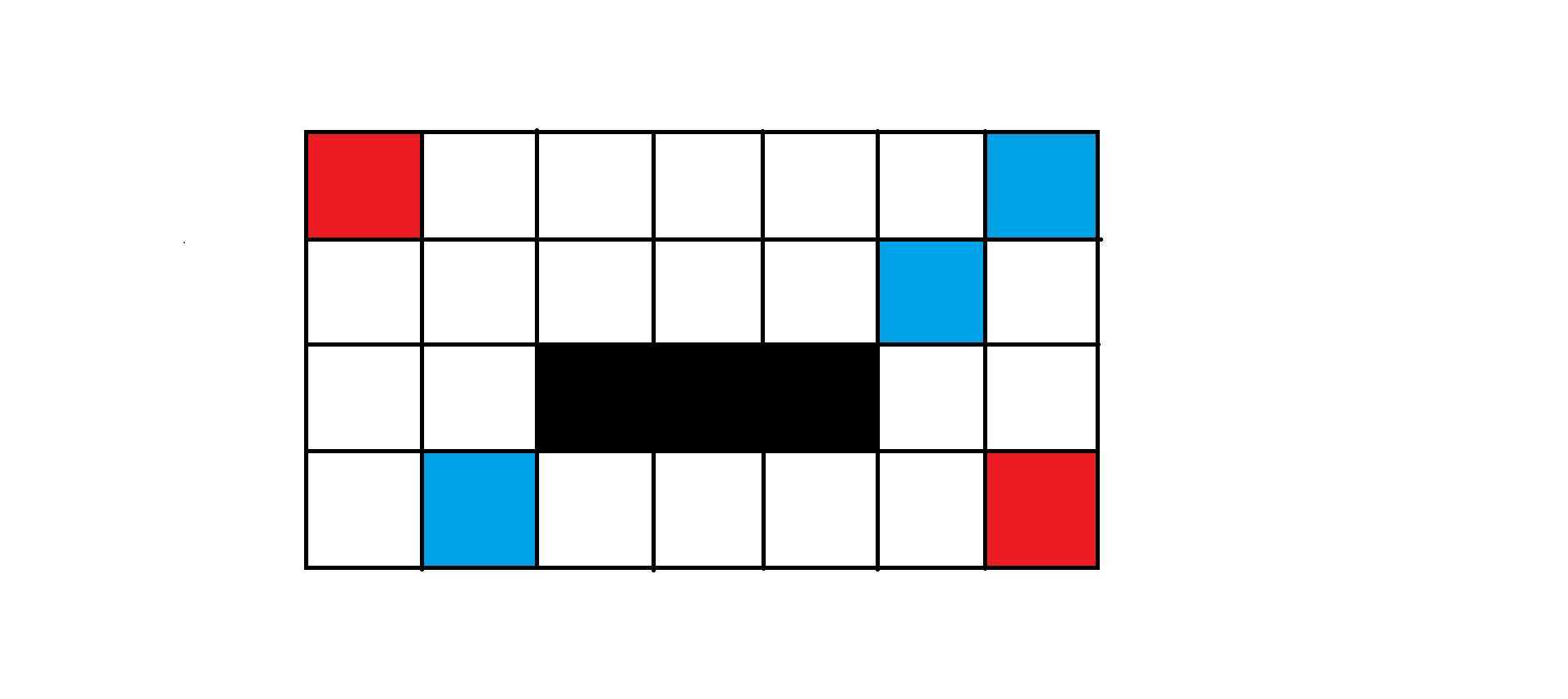
因为最右边只能向下,最左边只能向右,所以只要不走到坑里,就一定可以走到终点,所以考虑如何不走到坑里。如图所示,黑色区域为坑,要想不走到坑里,就必须走到蓝色的格子,就是坑的左下到右上对角线的格子。而且蓝色的格子是不相交的,即不存在一条路径同时经过两个蓝色节点。所以只需要统计走到所有蓝色格子的概率之和就是答案了。
然后就是求概率的问题,一个矩阵,从(1,1)走到(x,y)的路径总数为
因为共有x+y-2个选择向右或向下的位置,选择好向右(向下)后向下(向右)的位置也自然确定了。
这是路径总数,因为是随机选择,所以走某一条路径的概率是
所以走到非边界格子(x,y)的概率为
而边界格子因为下边界只能向右,右边界只能向下,所以就不是随机选择了,所以用递推处理一下
但是现在还有一个问题,数据范围太大,求组合数会爆精度。
所以用对数处理一下
这样所有问题就都解决了,总体复杂度O(N),N=Max(n,m)
#include<bits/stdc++.h>
using namespace std;
const int MAX=2e5+5;
double logfac[MAX],ym[MAX],xn[MAX];
double cal(int x,int y)
{
return exp(logfac[x+y-2]-logfac[x-1]-logfac[y-1]-(x+y-2)*log(2));
}
int main()
{
int T,cas=0;
scanf("%d",&T);
for(int i=1;i<=2e5;i++)
logfac[i]=logfac[i-1]+log(i);
while(T--)
{
int n,m,l,r,u,d;
double res=0;
scanf("%d%d%d%d%d%d",&n,&m,&l,&u,&r,&d);
ym[1]=pow(0.5,m-1);
xn[1]=pow(0.5,n-1);
for(int i=2;i<=n;i++)ym[i]=ym[i-1]+0.5*cal(m-1,i);
for(int i=2;i<=m;i++)xn[i]=xn[i-1]+0.5*cal(n-1,i);
for(int i=1;;i++)
{
int x=l-i,y=d+i;
if(x<1||y>m)break;
if(x==1)res+=pow(0.5,x+y-2);
else if(y==m)res+=ym[x];
else res+=cal(x,y);
}
for(int i=1;;i++)
{
int x=r+i,y=u-i;
if(x>n||y<1)break;
if(y==1)res+=pow(0.5,x+y-2);
else if(x==n)res+=xn[y];
else res+=cal(x,y);
}
printf("Case #%d: %.10f\n",++cas,res);
}
}
Google Kick Start 2020 Round B
原文:https://www.cnblogs.com/cryingrain/p/12824527.html