在数论中，欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则:
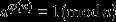于是就有公式：
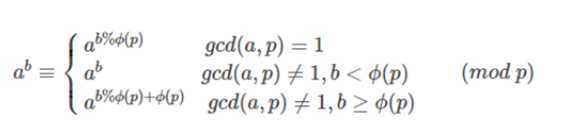
第一个要求a和p互质，第二个和第三个是广义欧拉降幂，不要求a和p互质，但要求b和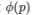
的大小关系。
问题：求2^(2^(2^(2^(2^...)))) mod p的值
题解：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll ph(ll x)
{
ll res=x,a=x;
for(ll i=2;i*i<=x;i++)
{
if(a%i==0)
{
res=res/i*(i-1);
while(a%i==0) a/=i;
}
}
if(a>1) res=res/a*(a-1);
return res;
}
ll quick_pow(ll a,ll b,ll mod)
{
ll ans=1;
while(b)
{
if(b&1) ans=(ans*a)%mod;
a=(a*a)%mod;
b>>=1;
}
return ans;
}
ll f(ll p)
{
if(p==1) return 0;
ll k=ph(p);
return quick_pow(2,f(k)+k,p);
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
ll p;scanf("%lld",&p);
printf("%lld\n",f(p));
}
return 0;
}
求A^B mod C
代码：
#include <bits/stdc++.h>
#define ll __int64
#define mod 10000000007
using namespace std;
char a[1000006];
ll x,z;
ll quickpow(ll x,ll y,ll z)
{
ll ans=1;
while(y)
{
if(y&1)
ans=ans*x%z;
x=x*x%z;
y>>=1;
}
return ans;
}
ll phi(ll n)
{
ll i,rea=n;
for(i=2;i*i<=n;i++)
{
if(n%i==0)
{
rea=rea-rea/i;
while(n%i==0)
n/=i;
}
}
if(n>1)
rea=rea-rea/n;
return rea;
}
int main()
{
while(scanf("%lld %s %lld",&x,a,&z)!=EOF)
{
ll len=strlen(a);
ll p=phi(z);
ll ans=0;
for(ll i=0;i<len;i++)
ans=(ans*10+a[i]-‘0‘)%p;
ans+=p;
printf("%lld\n",quickpow(x,ans,z));
}
return 0;
}
原文：https://www.cnblogs.com/jaszzz/p/12824619.html