支撑向量机,SVM(Support Vector Machine),其实就是一个线性分类器。——图片更加直接,会涉及到正则化
首先,我们看一个简单的二分类问题。在二维的特征平面中,所有的数据点分为了两类:蓝色圆形和黄色三角。我们的目标是找到了一条决策边界,将数据分类。但实际上我们可以找到多条决策边界。

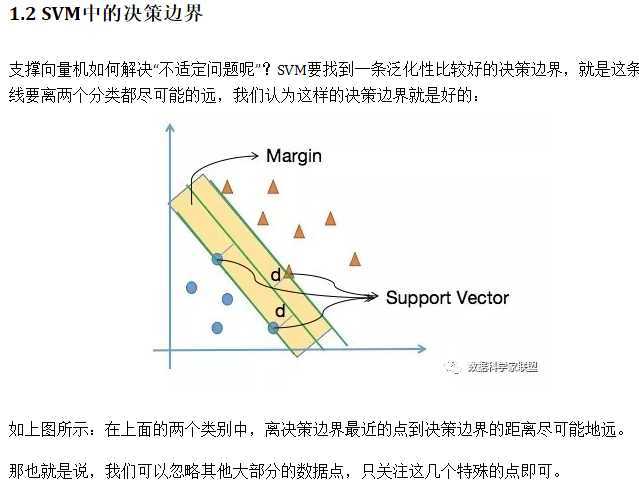
将最优决策边界向上&下平移,在遇到第一个点时停下来,这个点被称为支撑向量Support Vector;支撑向量到决策边界的距离是d;这两条平移后的直线的间隔(2d)被称为最大间隔Margin。
支撑向量就是支撑着两条平移边界的点,我们只需要重点研究这几个支撑向量即可,这也是SVM名称的由来;Margin就是分界面可以移动的范围,范围越大表示容错能力越强。
所以我们可以看到,所谓的支撑向量机,最初就是一个线性分类器,只不过这个线性分类器不仅能把样本分对,可以最大化Margin。
到目前为止,我们就将SVM转换为了一个最优化问题,下面的工作就是求出Margin的数学表达式,即将支撑向量机思想转化为数学问题。

其实我们可以看到,SVM算法也没有多么神秘。其最核心的思想就是从Input Space向更高维的Feature Space的映射,进行有Margin的线性分类。
在这一篇文章中,我们要做的就是学习支持向量机算法的相关概念、算法思想、推导过程。一边体会算法的奥义,一边为后续的进一步学习做准备。
在线性可分问题中,对于样本点来说,存在一根直线可以将样本点划分,我们称之为Hard Margin SVM;但是事实上,并不是所有情况都是完美的,这就引出了下一篇文章就讲解Soft Margin SVM以及相关知识。大家加油!


我们观察上面的表达式的形式,其实相当于在Soft Margin SVM中加入了L1正则。可以将理解为正则化项,避免因为训练出的模型往极端的方式发展,让模型的拥有一定的容错能力,泛化性有所提升。


SVM思想也可以解决回归问题。回归问题的本质就是找到一根能够很好滴拟合数据点的线(直线、曲线)。**不同回归算法的关键是怎么定义拟合。**比如我们之前学习的线性回归算法,定义拟合的方式就是数据点到拟合直线的MSE最小。
而对于SVM算法来说,如何定义“拟合”呢?
指定一个Margin值,在Margin区域的范围内,包含的数据点越多越好。这就表示这个Margin范围能够比较好地表达样本数据点,在这种情况下取中间的直线作为真正回归结果,用它来预测其他点的y值。
这和SVM算法解决分类问题的思路是相反的,在解决分类问题时,我们期望Margin中的范围越少越好。但是解决回归问题恰恰相反,我们希望所定义的Margin范围能够拟合更多的数据。
在具体训练SVM解决回归问题时,需要指定Margin范围,这里就引入了一个超参数,即Margin的边界到中间直线的距离。
那么这种思想如何转换成具体的最优化问题表达式极其推导,就不介绍了。我们直接看看如何在sklearn中使用它。
入门支持向量机系列终于写完了,这里做一个总结:SVM算法是一个很优秀的算法,在集成学习和神经网络之类的算法没有表现出优越性能前,SVM基本占据了分类模型的统治地位。目前则是在大数据时代的大样本背景下,SVM由于其在大样本时超级大的计算量,热度有所下降,但是仍然是一个常用的机器学习算法。
SVM算法的主要优点有:
SVM算法的主要缺点有:
原文:https://www.cnblogs.com/wjAllison/p/12825174.html