把样本到每个类的距离作为决策模型,将测式样本判定为与其距离最近的类
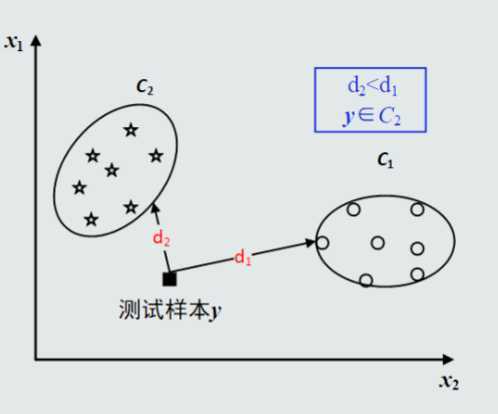
n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的欧氏距离(两个n维向量):

n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离:
对每维特征设置不同的权重
MED分类器是最小欧氏距离分类器
距离衡量:欧氏距离
类的原型:均值
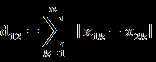
对于两个类来说MED分类器的决策方程为
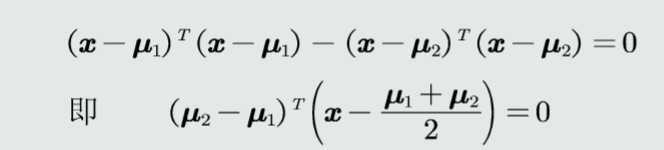
在高维空间中,该决策边界是一个超平面,垂直平分两个类原型的线
C1={(5,4),(7,0),(3.5,1),(4.5,3)}
C2={(4,4),(8,5),(8,3),(12,4)}
判断y=(4,5)所属的类别
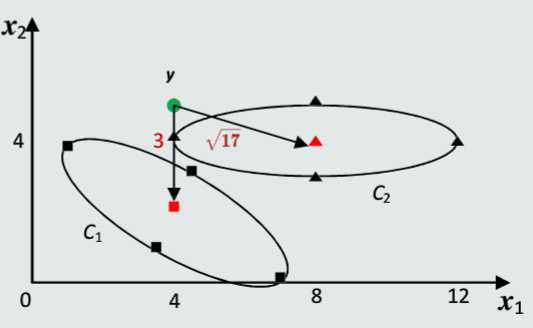
所以由图可得,y属于C1类
但本图中,直观上y更接近于C2类。
因为MED分类器没有考虑特征变化的不同以及特征之间的相关性。
目的:将原始特征映射到新的一个特征空间,使得在新空间中特征的协方差为单位矩阵,从而去除特征变化的不同及特征之间的相关性
将特征转化分为两步:先去除特征之间的相关性(解耦),然后再对特征进行尺度变化(白化)
令W=W1W2
解耦:通过W1实现协方差矩阵对角化,去除特征之间的相关性
白化:通过W2对上一步变换后的特征再进行尺度变换实现所有特征具有相同方差
得到W1:
1、求协方差矩阵的特征值和特征向量
2、由特征向量构建转换矩阵W1
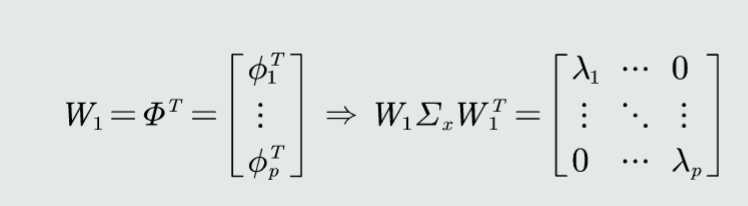
W2的求解:
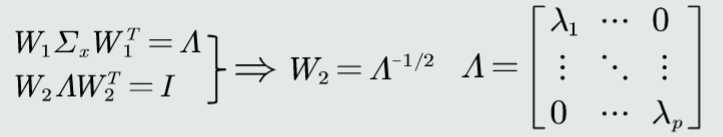
W的求解:
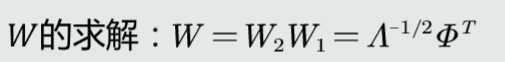
W转化后的欧氏距离为
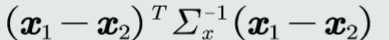
为马氏距离
马氏距离表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧氏距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的)并且是尺度无关的。
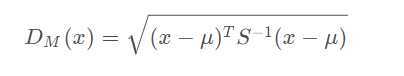
如果S?1是单位阵的时候,马氏距离简化为欧氏距离。
马氏距离的缺点:夸大了变化微小的变量的作用。受协方差矩阵不稳定的影响,马氏距离并不总是能顺利计算出。
马氏距离有很多优点: 马氏距离不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关;由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。
当求距离的时候,由于随机向量的每个分量之间量级不一样,比如说x1可能取值范围只有零点几,而x2有可能时而是2000,时而是3000,因此两个变量的离散度具有很大差异
马氏距离除以了一个方差矩阵,这就把各个分量之间的方差都除掉了,消除了量纲性,更加科学合理。
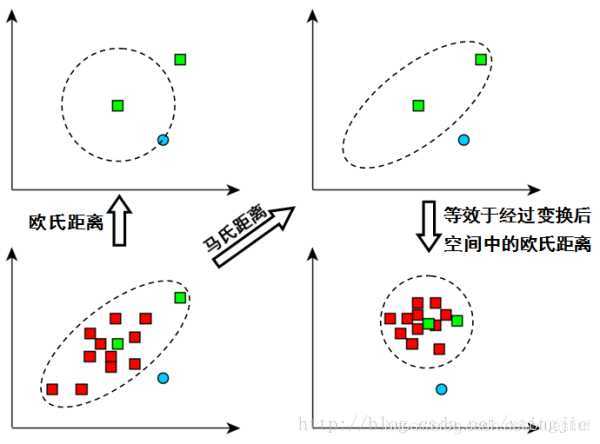
如上图,看左下方的图,比较中间那个绿色的和另外一个绿色的距离,以及中间绿色到蓝色的距离
如果不考虑数据的分布,就是直接计算欧式距离,那就是蓝色距离更近
但实际上需要考虑各分量的分布的,呈椭圆形分布
蓝色的在椭圆外,绿色的在椭圆内,因此绿色的实际上更近
马氏距离除以了协方差矩阵,实际上就是把右上角的图变成了右下角
距离度量:马氏距离
类的原型:均值
判别公式如下:
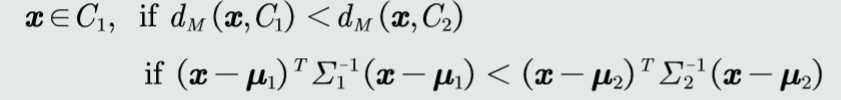
对于二类分类而言,MICD分类器的决策边界位于到两个类的距离相等的面上即:
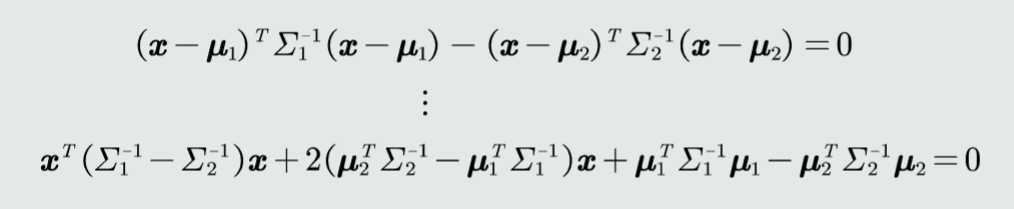
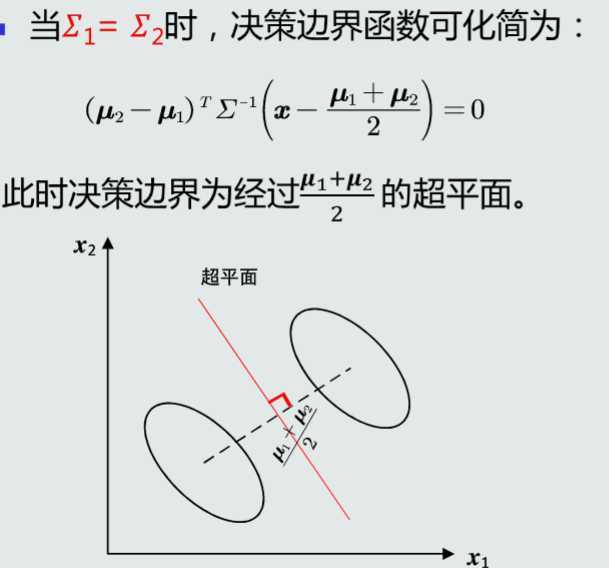
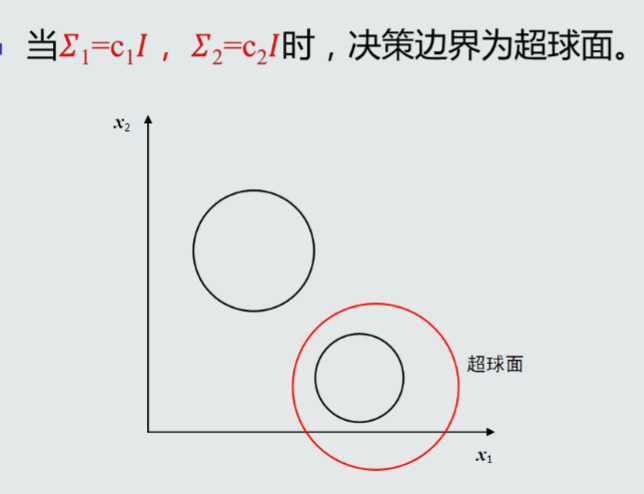
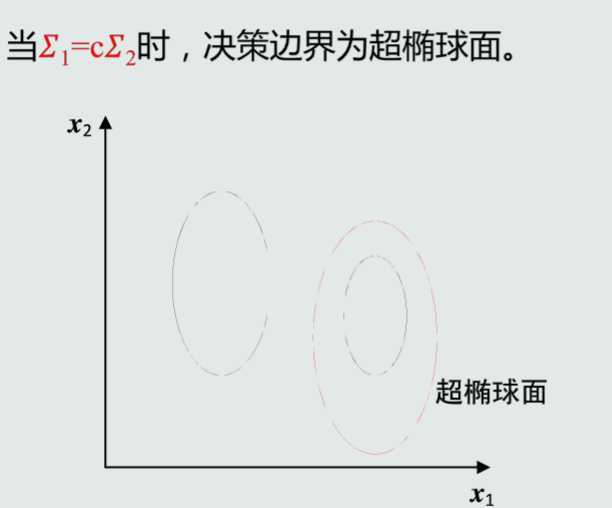
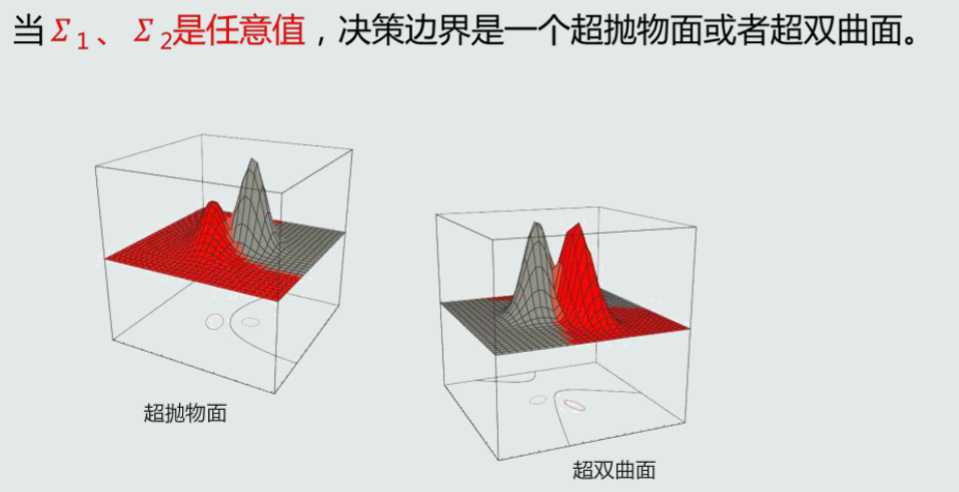
MICD分类器会选择方差较大的类
原文:https://www.cnblogs.com/zhanglingxin/p/12828618.html